基于预信号的交叉口公交相位插入策略设计
2013-12-26华璟怡
华璟怡 任 刚 于 晨
(东南大学交通学院,南京210096)
面对我国城市交通压力持续增加、交通拥堵日趋严重的现状,作为公交优先重要组成部分的公交信号优先(transit signal priority,TSP)能够有效减少公交车辆在交叉口的延误,提高其准点率和服务水平.在TSP的几类控制方法中,主动式公交信号优先具有能够根据实时状况调整控制参数、易于在工程实践中运用等优点,因此在欧美国家得到了广泛的运用,并取得了很大的成功[1].
目前国内外对主动式单点公交信号优先的研究主要集中在绿灯延长和红灯缩短这2种策略的控制逻辑[2-5]设计及延误分析[6-9]上,而对其他策略的研究较少.在欧美国家交叉口大量采用两相位信号控制的情况下,绿灯延长和红灯缩短能够有效地减少公交车辆在交叉口的延误.但对于我国主要交叉口采用的多相位信号控制方式,这2种策略缺乏对通行方向为红灯信号且下一个执行相位仍为红灯信号的进口道上公交车辆的优先服务.
本文将采用主动式单点公交信号优先中公交相位插入策略来解决上述问题,并提出以预信号的方式来实现这一策略的实际运用.
1 公交相位插入策略
公交相位插入策略是在正常的相位相序中为公交车辆增加一个特定的相位[10].其作用原理如图1所示:当车辆检测器检测到公交车辆到达交叉口时,若公交车辆的通行方向为红灯信号,且交叉口当前相位的下一个执行相位仍不允许公交车辆通过时,在当前相位和下一相位之间插入一个公交专用相位,为公交车辆提供信号优先.

图1 公交相位插入策略作用原理
另一方面,相位最大压缩时间是执行公交相位插入策略的关键,而相位最大压缩时间取决于各相位的交通状态.如图2所示,根据交叉口进口道绿灯时间内车辆通过时车头时距的变化情况,可以将绿灯时间g划分为饱和绿灯时间ga和富裕绿灯时间gb两个阶段,富裕绿灯时间即为该相位的最大压缩时间.对于公交相位插入策略而言,通过压缩当前相位和下一相位的富裕绿灯时间,对后续相位的富裕绿灯时间进行调整,以此来提供插入公交相位的通行时间.

图2 交叉口进口道排队累积示意图
2 策略设计
2.1 预信号控制下交叉口进口道设置
预信号控制方法是在交叉口进口道的通行区域内设置前后2条停车线,通过设置在后一条停车线上的预信号来控制非优先车辆的通行.即预信号为红灯时,非优先车辆在预信号控制停车线之后等待,而公交车辆可以直接进入主信号控制的前一条停车线之后的公交候驶区排队等待[11].
公交相位插入策略的实施需要在正常的相位相序中增加一个相位,由于公交车辆混杂在非优先车辆中,因此插入相位的持续时间难以确定.对此,本文考虑运用预信号控制方法将公交车辆从非优先车辆中分离出来,仅为公交车辆提供优先信号,实现策略的实际运用.
针对我国多相位信号控制交叉口冲突车辆的时空分离、交叉口公交专用车道未普遍设置及右转车道排队较少的特点,本文设计了如图3所示的预信号控制下交叉口进口道的设置方法:当公交车辆行驶至交叉口,发现预信号为红灯时,公交车辆将通过右转车道进入公交候驶区,等待优先控制系统判断是否插入公交相位.

图3 利用右转车道实现预信号控制的布局方法
2.2 控制逻辑设计
当检测器检测到公交优先申请时,优先控制系统能够根据交叉口的实际情况判断是否提供优先信号及分配各相位的压缩时间,本文设计策略的逻辑控制如图4所示.

图4 公交相位插入策略的控制逻辑图
2.3 控制参数确定
针对控制逻辑设计中需要确定各相位压缩时间的要求,本文提出了压缩时间确定方法:保证交叉口各进口道上车辆不会因为策略的实施而二次停车;能够根据相位持续时间按比例分配压缩时间,均衡各进口道交通负荷.假设交叉口的信号控制为n相位,则控制参数模型可分为如下3种.
1) 当前相位压缩时间gxi
通过压缩当前相位为公交相位提供通行时间,即
gxi=min(gx,gbi,gt)
(1)
式中,gx为插入公交相位持续时间;gbi为相位i的富裕绿灯时间;gt为相位结束时刻ts与公交到达停车线时刻t0之差.

(2)
(3)


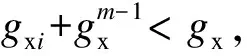
(4)
(5)
(6)
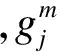
3 交通效益评价
3.1 车均延误计算模型
设公交车流饱和流率为sb,非优先车流饱和流率为sn,公交车流流率为qb,非优先车流流率为qn,周期长度为T,周期内红灯时间为r,公交相位插入时刻为t1,插入公交相位时间为gx.通过排队累积图示法对基于预信号的公交相位插入策略的正负交通效益进行分析.
根据图5中延误三角形的几何关系,可以得到公交车辆车均延误降低量的计算公式为

(7)
根据图6中延误三角形的几何关系,可以得到非优先车辆车均延误增加量的计算公式为
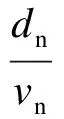
(8)
3.2 延误对比分析
假设一交叉口为四相位信号控制,其参数为T=120 s,每一相位持续时间为30 s,gx=5 s,sb=1 000 veh/h,sn=1 600 veh/h.同时,假设饱和度w在0.50~0.90之间变化,公交车流流率qb=250wveh/h,非优先车流流率qn=400wveh/h.
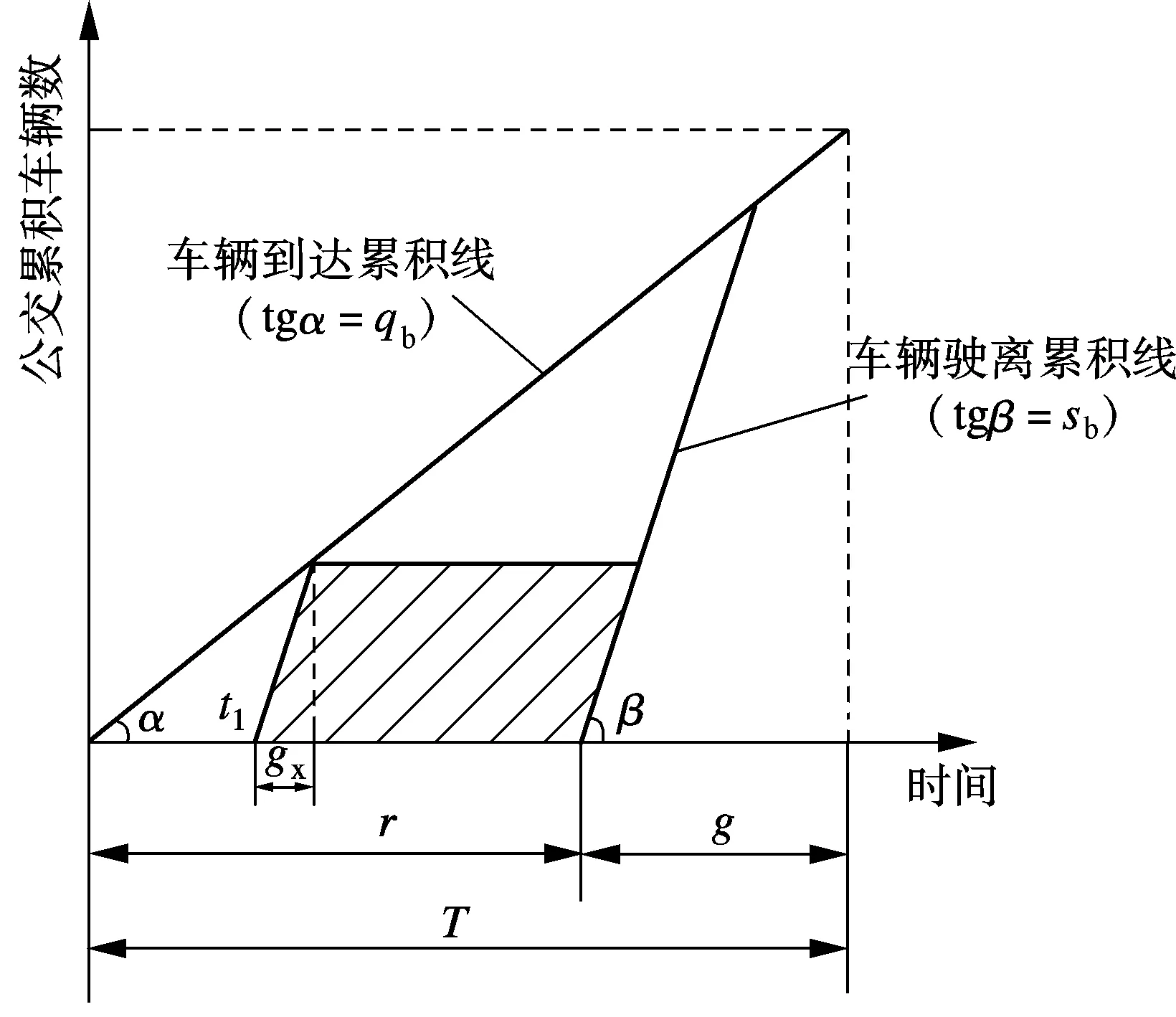
图5 公交车辆延误分析

图6 非优先车辆延误分析
根据式(7)、(8)计算得到公交车辆车均延误减少量及非优先车辆车均延误增加量(其中公交相位插入时刻分为25及55 s两种),如表1所示.

表1 策略效果与交叉口饱和度的关系
可以看出,在执行公交相位插入策略的情况下,不同交叉口饱和度公交车辆的车均延误减少量均超过了非优先车辆的车均延误增加量,因而证明策略是有效的.且非优先车辆车均延误增加量均不超过5 s,对交叉口的整体服务水平影响不大,与此同时,在较低的交叉口饱和度条件下,公交车辆的服务水平却有极大的增加.另一方面,随着交叉口饱和度的提高,执行策略的效果不断下降,当交叉口饱和度超过0.9后,策略的恢复期很长,执行效果不再明显,且会带来损失时间的增加及交叉口复杂程度的提高,这也验证了交叉口饱和度应不大于0.9的判断.
4 仿真验证
为进一步验证基于预信号的公交相位插入策略的有效性,本文采用VISSIM3.70微观仿真软件对南京市丹凤街-大石桥街四相位交叉口策略执行前后分别建立仿真模型,并对公交车辆平均延误及非优先车辆平均延误进行前后对比分析.
交叉口4个进口道的几何布局形式均为:3个专用进口车道(左转、直行、右转各一)和2个出口车道.交叉口的信号配时为南北直行(37 s)、南北左转(17 s)、东西直行(29 s)、东西左转(13 s).所有车辆右转均无限制.实际调查流量如表2所示.

表2 丹凤街-大石桥街交叉口高峰小时流量表 veh/h
在仿真阶段,每次仿真时段取4 000 s,其中包括400 s路网车流初始化阶段.由于仿真的随机性,在本次仿真中对方案做10次仿真运行.运行得到延误对比如表3所示.

表3 非优先车辆延误仿真对比 s/veh
从表3中可以看到,10次策略实施前后的仿真对比中,公交车辆的车均延误平均值由26.82 s下降为16.22 s,降幅接近40%;同时,策略执行下非优先车辆的车均延误平均值由26.82 s上升为30.61 s,升幅不到15%.相比于交叉口公交车辆服务水平,则由C级提升为B级,非优先车辆服务水平维持在C级不变,策略的实施对交叉口的整体运行影响不大.
5 结语
本文研究了一种适用于多相位信号控制交叉口的公交相位插入策略的设计、评价与仿真.策略运用了预信号控制方法实现实际运用,并通过控制参数计算模型保证各进口道不会超饱和.同时,为保证交叉口运行的平稳性,本文提出的优先策略仅为在正常配时下到达的公交车辆提供信号优先,而对于在策略恢复期到达的车辆,无法实现优先.最后,策略的效益评价和实例仿真的结果表明,策略的实施能够在不显著增加非优先车辆延误的同时,有效减少公交车辆的延误;但策略的效益会随着交叉口饱和度的增加而降低,当交叉口饱和度超过0.9后,策略的实施将失去意义.
)
[1] Baker R J, Chang J, Smith H R. An overview of transit signal priority [R]. Washington DC: ITS America, 2003.
[2] Agrawal B B, Waller S T, Athanasios Z. Modeling approach for transit signal preemption [J].TransportationResearchRecord, 2002,1791: 13-20.
[3] Vlachou K, Collura J, Mermelstein A. Planning and deploying transit signal priority in small and medium-sized cities: Burlington, Vermont, case study [J].JournalofPublicTransportation, 2010,13(3): 101-123.
[4] Eleni C, Alexander S. Traffic signal optimization with application of transit signal priority to an isolated intersection [J].TransportationResearchRecord, 2011,2259: 192-201.
[5] 柳祖鹏,李克平,倪颖. 基于绿灯需求度的单点公交信号优先控制策略[J]. 同济大学学报:自然科学版, 2013, 41(3): 408-414.
Liu Zupeng, Li Keping, Ni Ying. Isolated transit signal priority control strategy based on demand degree of green [J].JournalofTongjiUniversity:NaturalScience, 2013,41(3): 408-414. (in Chinese)
[6] Heydecker B G. Capacity at a signal-controlled junction where there is priority for buses [J].TransportationResearchPartB, 1983,17(5): 341-357.
[7] Larry H, Douglas G, Zhiping W. Decision model for priority control of traffic signals [J].TransportationResearchRecord, 2006,1978: 169-177.
[8] 马万经,杨晓光. 单点公交优先感应控制策略效益分析与仿真验证[J]. 系统仿真学报, 2008, 20(12): 3309-3311.
ma Wanjing, Yang Xiaoguang. Efficiency analysis of transit signal priority strategies on isolated intersection [J].JournalofSystemSimulation, 2008,20(12): 3309-3313. (in Chinese)
[9] Wanjing M, Xiaoguang Y, Yue L. Development and evaluation of a coordinated and conditional bus priority approach [J].TransportationResearchRecord, 2010,2145: 49-58.
[10] 谭摇真,黄志义,梅振宇. 主路协调下单点TSP策略关键控制参数仿真优化[J]. 交通运输系统工程与信息, 2012, 12(4): 64-71.
Tan Yaozhen, Huang Zhiyi, Mei Zhenyu. Simulation of key control parameters with TSP strategies and artery coordination on isolated intersections [J].JournalofTransportationSystemsEngineeringandInformationTechnology, 2012,12(4): 64-71. (in Chinese)
[11] 张卫华,王炜. 基于公交优先通行的交叉口预信号设置方法研究[J]. 公路交通科技, 2004, 21(6): 19-23.
Zhang Weihua, Wang Wei. Study on design methods of pre-signals based on bus priority of intersections [J].JournalofHighwayandTransportationResearchandDevelopment, 2004,21(6): 19-23. (in Chinese)
