SCR谐振半桥式拓扑设计
2013-12-23余云昊张建峡
刘 跃,余云昊,张建峡
(贵州大学实验室与设备管理处,贵州贵阳 550003)
1 SCR及半桥式电路
半桥式电路可工作于串联负载状态。在串联负载电路中,由于电路无需输出电感,因此在输出高压或低压的场合都适用。该电路可以安全地承受输出端短路,但是输出端不能开路。半桥式电路也可以工作在并联负载状态,输出负载通过变压器折算到初级,和谐振电容并联[3]。此时电路输出端可以开路,但是不可以短路。串联负载电路可以作为驱动变压器初级的电流源进行分析,而并联负载电路可以作为驱动变压器初级的电压源进行分析。当要求输出直流时,并联负载电路需要次级输出电感,但对输出电压波纹要求不高时也可以省略[4-5]。因此,对于DC/DC 变换器,串联负载电路是个更好的选择。
本文通过对串联负载SCR 谐振半桥式变换器的基本工作原理的分析,给出了该变换器的设计的计算方法,并给出了设计实例,完成了对SCR 谐振半桥式拓扑的设计。
2 串联负载SCR谐振半桥式变换器的基本工作原理
图1是串联负载SCR 谐振半桥式电路,其主要波形如图2所示。由图1可见,当Q1被触发导通时,环路形成,C1上幅值为Vdc/2 的电压加到L3、L1和C3组成的串联谐振电路上。其中由T1次级折算到初级的阻抗和T1的励磁电感并联。
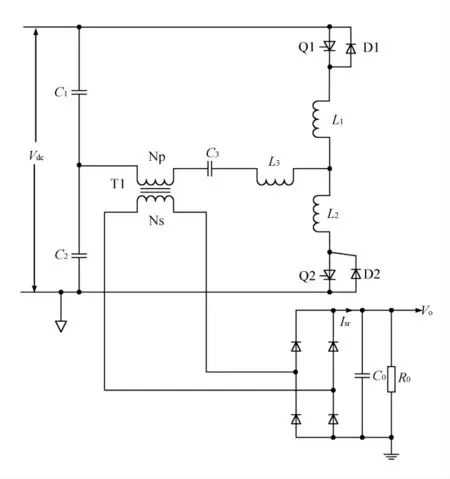
图1 串联负载SCR 半桥式电路
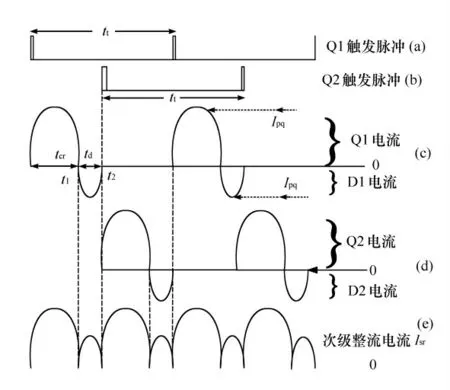
图2 电流波形
图2为串联负载SCR 谐振半桥式电路(见图1)在直流输入电压最小、负载最大时的主要波形。其中tcr为SCR 的导通时间,td为反并联二极管的导通时间,Ipq为电路电流峰值,tt为触发周期。如图1所示,晶体管Q1和Q2轮流导通半个周期。当Q1导通时,电容C3与L3及L1(L2=L1)发生谐振;当Q2 导通时,C3与L3及L2发生谐振。只要触发其中一个SCR,就会流过正弦半波电流,然后电流过零反向,以正弦半波规律流经其反并联二极管。如果二极管电流的持续时间大于SCR 的电路换向关断时间tq值,SCR 就能自动关断。当输入电压或者负载电阻增大时,反馈环就会减小触发频率,以增大Q1和Q2的正弦电流波的时间间隔,从而维持平均输出电流和电压恒定[2]。
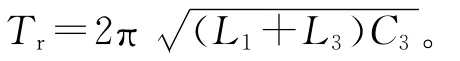
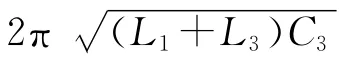
在直流输入电压最小和输出功率最大(输出负载电阻最小)时,电路也会维持图2所示的关系。谐振电感值和电容值的选择要使2(b)所示的电流幅值和时间间隔在电源电压最小和负载最大时在设定的输出电压范围内,能够满足所需平均输出电流的要求。后文将介绍满足上述要求的计算方法。电源电压或负载改变时,检测输出电压的反馈环将调节SCR 的触发频率ft以维持输出电压恒定[7]。电流峰值增大时,反馈环将降低ft,以维持次级平均电流恒定,从而维持输出电压恒定。而且,对于固定的直流输入电压和L、C值,电流峰值(图2(c)和图2(d))将是恒定的;如果R0增大,则反馈环将降低ft以维持平均输出电压恒定。正常的直流输入电压和负载下的相应波形如图3 所示。过高的电流峰值会迫使反馈环减小触发频率,以维持输出电压稳定。周期为
1.1 对象 2008年1月—2010年12月在我院行髂腹股沟淋巴清扫术的阴茎癌患者56例(共111个腹股沟手术区)。患者的中位年龄为51岁(20~79岁),其中,术前行新辅助放疗2例,行新辅助化疗10例;吸烟者17例,酗酒者2例;糖尿病患者4例。16例患者的体质指数(BMI)超过25。
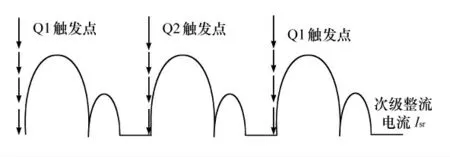
图3 高输入电压下的整流桥输出电流Isr
3 串联负载SCR 谐振半桥式变换器的设计计算
首先要确定谐振周期或频率。假设使用Marconi ASCR 类型的ACR25U 芯片,根据该芯片的特性,当门极偏执电压为0V、通态电流为50A 时,其典型关断时间为5 μs。假设情况最坏时,关断时间延长20%,即6μs。同时假设电路输入电压最小、输出功率最大,且工作于连续模式的临界状态(如图2所示,二极管过零点与对应SCR 电流的开始时刻之间没有时间间隔)[8-9]。则由图2 可见,最小的谐振周期为12 μs,即最大谐振频率为83kHz。但由SCR 的特性可知,输出功率较大时二极管导通时间td将减小到一个难以预测的数值。若td小于tq,SCR 就可能无法正常关断,因而td应留有一定的裕量。而且,阳阴极间电压在导通时不能迅速下降到2~3V 的静态值。为使导通时阳阴极间高电压的持续时间只占SCR 导通时间tcr的一小部分,谐振半周期至少应为2.5μs的4倍。这使在正弦阳极电流峰值时刻阳阴极间电压约为3V,而这是一个合理折中的方案。因此谐振周期选择为20μs(谐振频率fr=50kHz),即
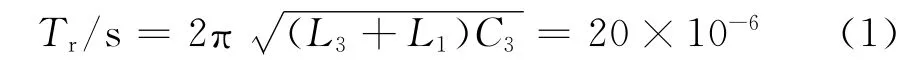
下面选择T1 初级(见图1)的电压峰值。根据Chambers在论文中的建议,其值应为一个桥电容(图1中的C1和C2)最小电压的60%,即
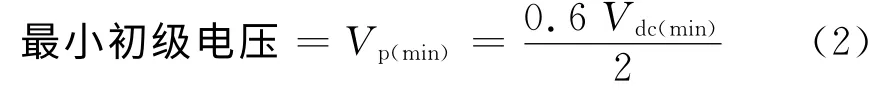
假设桥式输出整流器每个二极管的压降为1V,则可以确定T1的匝比为
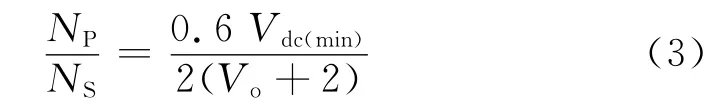
当电源电压最小,次级电流如图2(d)所示,反向二极管续流结束时刻和另一个SCR 的导通时刻之间没有时间间隔。假设在负载电流最大时,SCR 和二极管的导通时间约为半个周期,同时假设二级管电流峰值为SCR 的1/4,则图2(d)中SCR 和二极管电流的平均值为
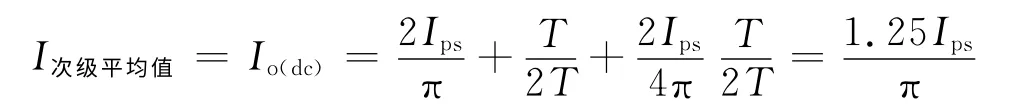
式中,Ips是初级SCR 电流峰值折算到次级的值,因而
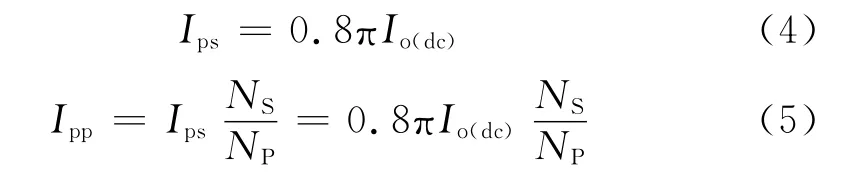
式中,Ipp是初级SCR 的电流峰值。
在图1 中,施加于串联谐振元器件上的电压为Vap,当Q1导通时,即为桥电容C1上的电压加上变压器的电压峰值0.6Vdc/2,即
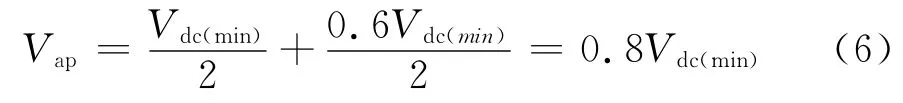
因此可大致推算,当阶跃电压Vap加到串联LC 电路上时,首个谐振电流脉冲的峰值为

本设计中,L=L1+L3,C=C3,则有
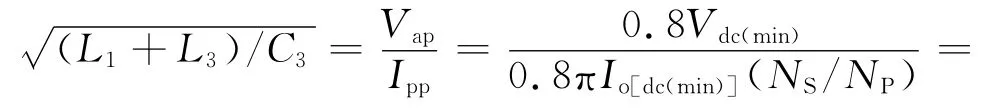
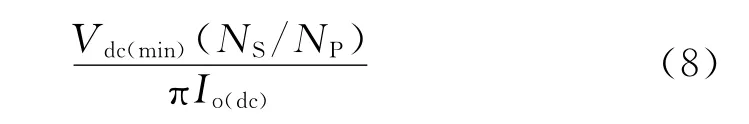
因此,由式(1)和式(8)给出的(L1+L3)和C3的关系,对于特定的Vdc(min)和最大输出电流Io(dc),可以确定谐振元件(L1+L3)或者(l2+l3)和C3的值,而变压器的匝比由式(3)确定。选择恰当的比值L3/L1,可以使SCR 所受的断态电压应力最小。比值越小则应力越小,dV/dt应力也越小,但最好依据经验值来选择。电感L3包括变压器初级漏感和杂散电感,但它的值的确定不宜过分依赖于漏感值,因为漏感值通常有较大的变化,这会导致谐振周期的变化过大。
4 串联负载SCR 谐振半桥式变换器的设计实例
假设图1中的电路性能指标如下:
输入功率:2 000 W
输出电压:48V
输出电流:Io(dc)
正常输入直流电压:310V
最大输入直流电压:370V
最小输入直流电压:270V
由式(3)可得
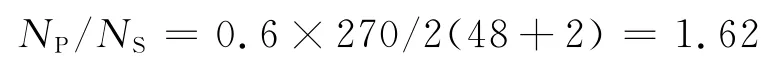
因Tr=20μs,由式(1)可得
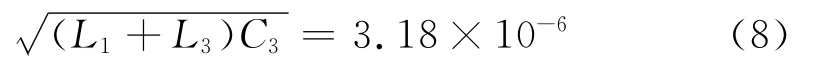
由式(8)可得
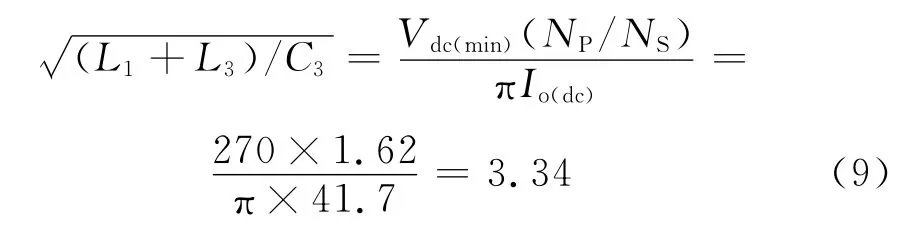
由式(8)和式(9)可得,C3=0.95μF,L3+L1=10.6 μH;由式(6)和式(7)可得
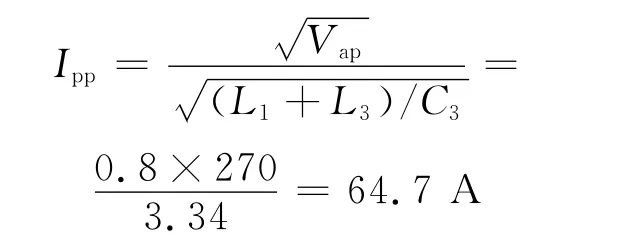
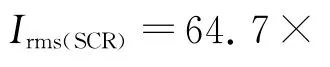
5 结论及展望
本文通过对串联负载SCR 谐振变换器的研究,给出了该变换器的设计方法,包括L、C 元件值的选择,谐振周期的选择,匝比的选择,对于输入电压波动的情况下,该设计不仅考虑到电路的特性,同时结合SCR的特性,给出了较合理的方案,完成了对该拓扑的设计。
(
)
[1]Martin I.Operating Characteristics of Self-commutated Sinewave SCR Inverters[M].RCA Application Note AN-6745,RCA,Somerville,N J,1978:15-17.
[2]Mapham N.An SCR Inverter with Good Regulation and Sine Wave Output[M].IEEE Transactions on Industry and General Applications,IGA-3(5),1967:33-35.
[3]张淼,冯垛生,谢俊杰.SCR-SPWM 变频调速系统[J].电力电子技术,1997,4(11):28-33.
[4]Chambers D.Designing High Power SCR Resonant Converters for Very High Frequency Operation[J].Proceeding Powercon 1982(9):22-24.
[5]华清.可控硅整流器:一种新型自动化元件[J].自动化学报,1966,4(3):176-196.
[6]张占松,蔡宣三.开关电源的原理与设计[M].北京:电子工业出版社,2007.
[7]Chambers D.A 30kw Series Resonant X Ray Generator[J].Powertechnics Magazine,1986(1):39-40.
[8]Bedford B D,Hoft R G.Principles of Inverter Circuits[M].New-York:Wiley,1964:11-14.
[9]Grafham D R,Hoft R G,Connolly A P.General Electric SCR Manual[M].6th ed.New York:General Electric Co,1979:9-10.
