表面波软组织黏弹性测量仿真的研究

林浩铭，陈思平，，汪天富

1)浙江大学生物医学工程与仪器科学学院，杭州310029;2)深圳大学医学院，广东省生物医学信息检测与超声成像重点实验室，深圳518060

生物组织的力学特性表征，包括硬度或弹性，与组织病理变化过程紧密相关［1］. 临床研究表明，呼吸系统病症会造成慢性肺纤维化，而肝纤维化和肝硬化最终可能导致肝衰竭，且伴随原发性肝癌.因此，发展准确可靠的生物组织力学特性测量方法成为迫切需要. 近年来，除了流变仪测量方法［2］，有学者相继提出多种基于超声技术的力学特性测量方法. 如准静态弹性成像［3-6］能提供反映组织弹性的二维映射图，可检测正常背景组织中的异常病变，但该方法无法评估弥散性病变. 声辐射力弹性成像［7-8］能定量测量局部组织的弹性，但却忽略了组织黏性信息. 剪切波频散振动［9-10］也能定量测量局部组织的黏弹性，但其剪切波假设应在无限大、均匀且各向同性介质中传播，在测量组织表面时尚欠准确. 该技术主要运用了Voigt 黏弹性模型，但由于Voigt 模型缺少应力松弛过程，而Maxwell 模型能描述应力松弛过程，却不能反映应变蠕变变化过程，这两个模型并不足以表征某些复杂的生物组织. Zener 黏弹性模型是Maxwell 模型与Voigt 模型的组合，可以同时反映蠕变与松弛过程，能更好地反映生物组织的力学特性. 本研究提出基于表面波的超声测量生物组织黏弹性的方法，通过引入Zener 黏弹性模型，推导出Zener 黏弹性模型组织中表面波频散速度与黏弹性参数的关系，采用有限元方法建立仿真验证模型.

1 理论基础

在各向同性的线弹性固体中，波动方程为［11］

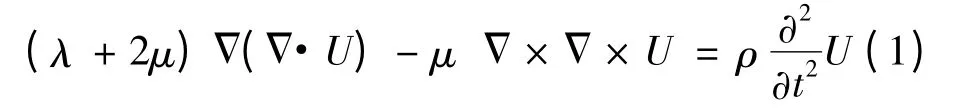
其中，λ 和μ 是介质的拉梅常数;ρ 是介质的密度;U是位移，其包括纵波位移分量与横向位移分量.

当只考虑波的横向分量时，频率相关的剪切波速度为

图1 为Voigt 黏弹性流变模型和Zener 黏弹性流变模型. 其中，μ、μ1和μ2为剪切模量;η 为黏性模量. 不同流变模型的复剪切模量亦不同，Voigt 黏弹性模型的剪切波速度为

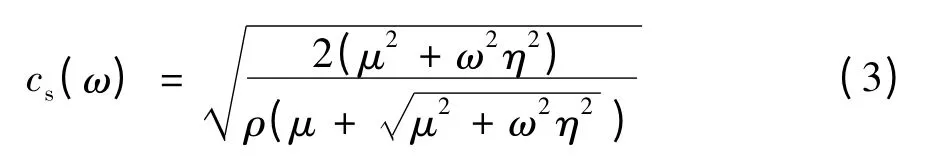
Zener 黏弹性模型［12］由2 个弹性元件和1 个阻尼元件组成，其复剪切模量为

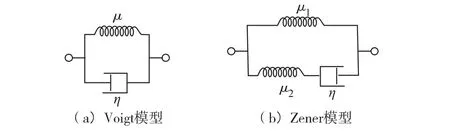
图1 黏弹性流变模型Fig.1 Viscoelastic Rheology Model

将式(4)代入式(2)，则Zener 模型的频散剪切波速为

在半无限大且各向同性的黏弹性介质空间中，表面波的传播速度c(ω)与剪切波速度cs(ω)的关系为［13］

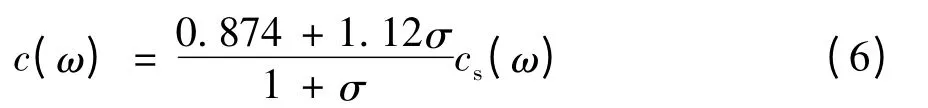
其中，σ 为介质的泊松比.

单频表面波速度可通过检测波在某一距离内的相位偏移，由式(7)估计得到.

其中，Δφ 是表面波在Δr 距离内的相位偏移;ω 是表面波的频率. 这样，通过估计不同频率的表面波速度，可得到其对应的剪切波速度，并运用非线性拟合方法逆向估计黏弹性参数. 在非线性拟合中，通过使式(8)最小求得模型参数.

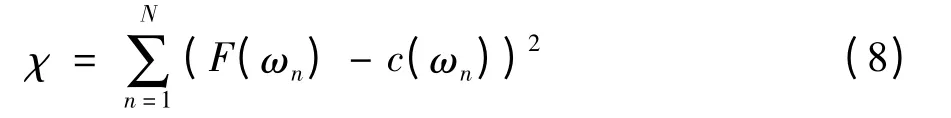
其中，F 为拟合函数;N 为频率的个数;ωn为频率.

2 表面波位移估计

表面波位移可通过发射一定脉冲重复频率的超声波检测并通过估计得到. 基于超声方法的位移估计可采用互相关或相移算法［14］实现，互相关方法虽能较准确地估计位移，但计算量大，而相移算法虽然准确度高，但不适合较大位移的估计. 因此，本研究采用互谱方法实现［15］位移估计，该方法具有稳定、快速及精确的优点. 设s(t)为发射的超声脉冲，其中心频率为f，S(f)是s(t)的频谱. 由于散射子的振动，相邻两帧的射频回波信号相对s(t)具有不同的时间延迟. 设第n 帧和第n +1 帧的回波信号分别为s(t - τn)和s(t - τn+1)，其对应频谱为

将式(8)取复共轭然后与式(9)相乘，得

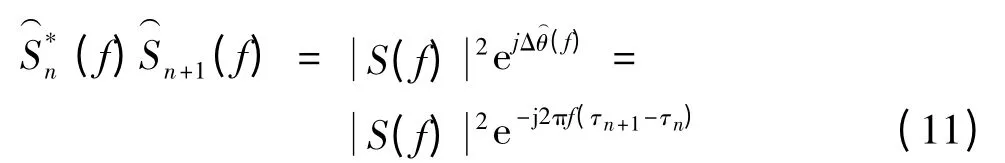
其中，Δd 为相邻两帧回波信号的时间间隔内散射子的位移差;T 为探测重复频率.

设散射子初始位移为d0，则散射子在第n +1 帧的位移dn+1为

当位移估计完成后，运用卡尔曼滤波算法［16］估计其相位，根据式(7)计得表面波速度，该过程如图2.

3 有限元仿真

图2 表面波位移与速度估计流程图Fig.2 Flow diagram of surface wave displacement and velocity estimation

运用Comsol 有限元仿真软件设计二维有限元模型，如图3. 有限元模型大小为0.2 m ×0.2 m，网格单元数为24 898，网格结点间平均距离为0.9 mm. 在仿真模型中，边界1 为自由边界条件，为保证对称性，边界2 和边界3 为周期性边界条件，边界4 为固定边界条件. 仿真区域内的材料属性设置ρ =1 055 kg/m2，σ =0.499. 在仿真模型中，选取Voigt 模型和Zener 模型作为黏弹性模型，参数设置如表1.

图3 仿真区域原理图Fig.3 Schematic diagram of simulation domain

表1 仿真黏弹性参数Table 1 Viscoelastic parameters for simulation

表1 中的黏弹性参数都可转化为用Prony 系数形式［17］. 在仿真中，通过对边界1 中间施加周期性单频振动来产生表面波传播，频率为100 ～400 Hz，相邻频率间隔为50 Hz，施加振动时间长度为5 个周期，施加外力使得最大位移幅度约为10 μm 数量级. 记录并保存距离振源1 ～20 mm，相隔1 mm 的20 个位置点处位移的垂直分量随时间的变化，用于仿真振动探测过程中，估计表面波速度. 在脉冲回波探测振动的仿真中，根据保存的位移数据产生振动散射点，并运用FieldⅡ仿真工具箱［18］实现对振动进行超声探测仿真. 在FieldⅡ仿真中，探测脉冲中心频率为2 MHz，探头带宽为60%，采样频率为100 MHz，脉冲重复频率被设为保证每个振动周期包括20 个探测脉冲，仿真得到的回波信号添加高斯白噪声使其信噪比为35 dB，仿真重复5 次.

4 仿真结果

如图4，对边界1 施加200 Hz 频率的垂直振动，将记录的20 个位置点随时间变化的垂直位移排列成二维图像，图像亮度表示位移幅度. 由图4可见，振动位移峰值约为20 μm，波峰随时间逐渐远离振源中心，又因存在黏性，振动位移随传播距离的增加而减小.

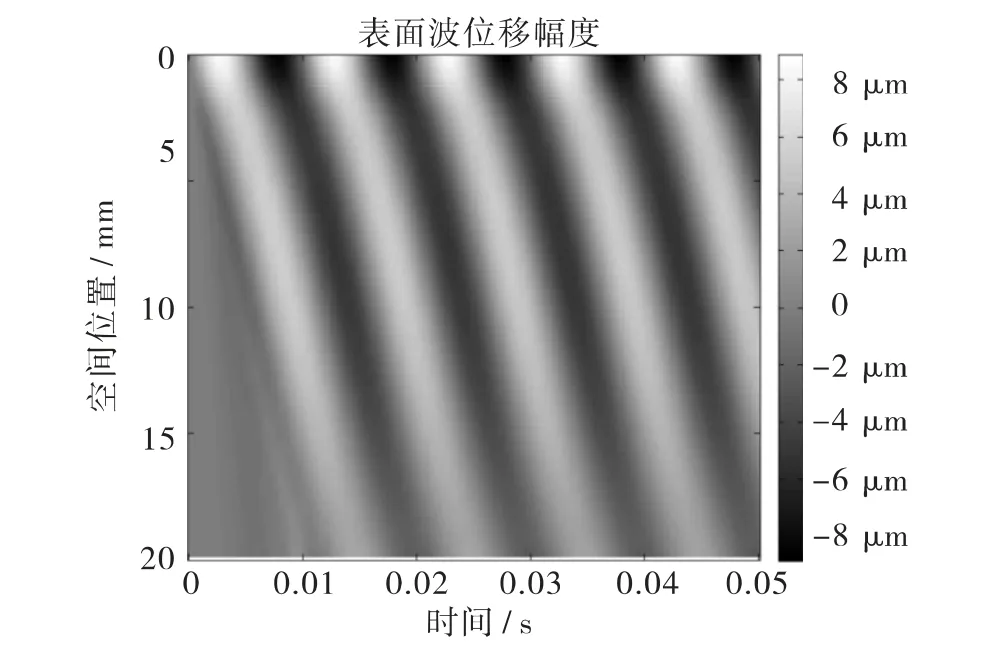
图4 不同位置点随时间变化的垂直位移Fig.4 Vertical displacement change with time of different position

图5 为振动点附近不同时刻的回波信号. 由图5 可见，由于质点的振动，回波信号间具有一定的时间偏移. 因此，振动位移可采用前述方法估计得到. 一旦完成位移估计，在表面波的传播方向上，各探测位置的振动可采用卡尔曼滤波算法进行跟踪，从而提取振动相位. 图6 为追踪结果，其中实线表示第1 个探测位置的振动点附近的振动位移估计，其振动频率为200 Hz;虚线为运用卡尔曼滤波算法对振动进行追踪得到的结果. 可见，该算法能准确追踪振动位移曲线，并估计振动相位. 为求得局部区域内波传播的平均速度，局部平均相位差可通过分别提取各个探测位置的振动相位，并在空间上做解卷绕处理后，用最小二乘方法拟合求得，结果如图7. 探测区域内的平均相位差即为拟合直线斜率的绝对值. 最后，采用式(7)估计得到表面波速度.

图5 不同探测时刻的回波信号Fig.5 Echo signal of different detection time

图6 振动位移跟踪结果Fig.6 Result of vibration displacement tracking

根据式(6)，对于泊松比σ =0.499，cs(ω)可由对应频率的c(ω)乘以比例因子1.05 得到. 对于仿真模型中设置的黏弹性模型和参数，采用上述方法估计得到的表面波速度和偏差如表2 和图8.

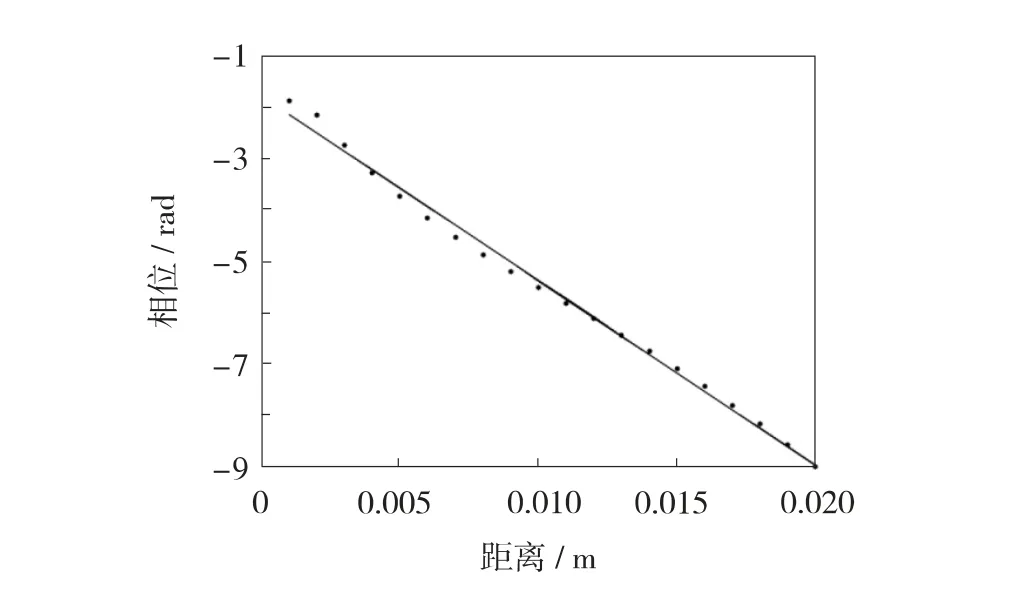
图7 不同探测位置振动相位拟合结果Fig.7 Fitting result of vibration phase of different detection positions

从表2 可见，对于所选Voigt 和Zener 模型，表面波速度估计与理论值较为接近，但仍存在微小偏差，表面波速度最小相对估计偏差分别为0.69%和0.52%，而最大相对估计偏差分别为3.39% 和3.05%. 原因可能有:①理论估计时要求表面波在半无限大空间中传播，而有限元仿真时的仿真区域是有限的;②当进行有限元仿真时，不同模型的黏弹性参数被近似转化为Prony 系数形式，可能产生误差;③噪音干扰使相位估计误差有可能造成表面波速度偏差，尤其是当频率较高时. 因此，表面波速度估计偏差在可接受范围内.

黏弹性参数可以由式(6)对100 ～400 Hz 的表面波速度进行非线性拟合获得，黏弹性参数估计结果及拟合接近程度参数χ，如表3，其计算如式(8). 从表3 可见，黏弹性参数估计结果与理论值较接近.

表2 仿真模型中表面波速度的理论值与估计值Table 2 Theory and estimated values of surface wave velocity for simulation model

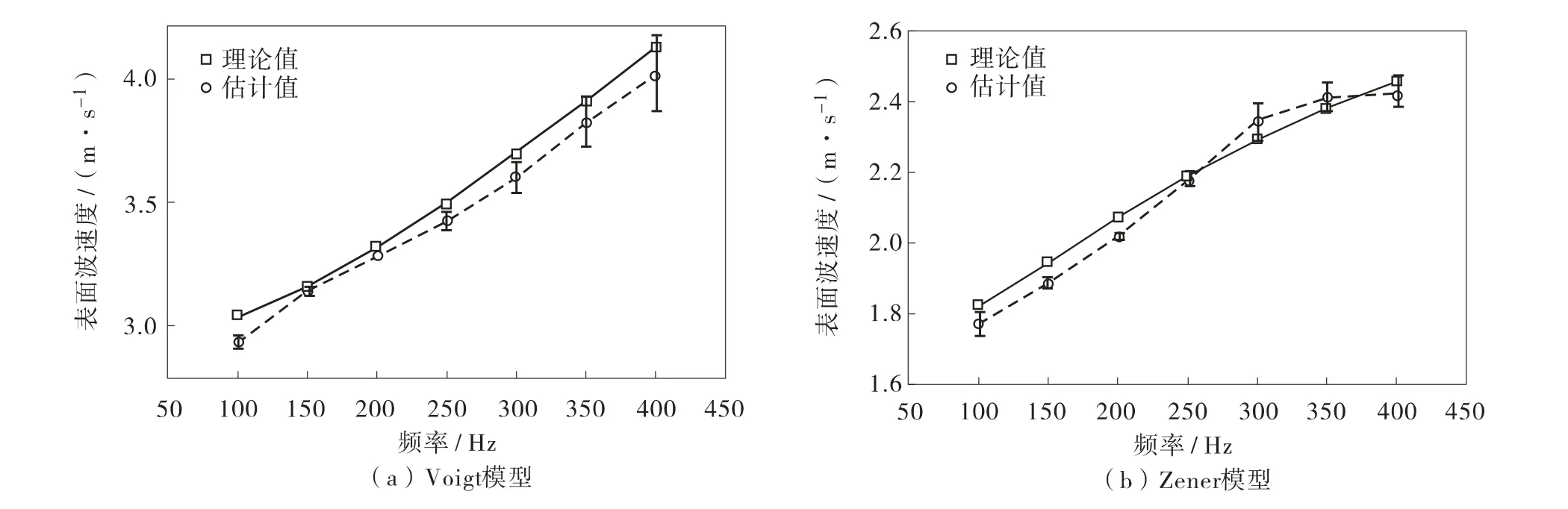
图8 不同频率表面波速度估计结果Fig.8 Estimated result of shear wave velocity of different frequency

表3 黏弹性估计结果Table 3 Result of viscoelasticity estimation

从式(6)可见，表面波速度与泊松比有关，对于表1 中的仿真模型，选择不同的泊松比参数进行仿真，表面波速度与黏弹性参数估计偏差结果如图9 和图10. 图9 中纵坐标为不同泊松比情况下各频率表面波速度估计偏差的平均值，对于Voigt 模型和Zener 模型，其表面波速度估计偏差的平均值为0.98%和0.83%. 图10 为在不同泊松比情况下的黏弹性参数估计偏差，对于Voigt 模型，剪切弹性μ 和剪切黏性η 估计偏差的平均值分别为3.78%和1.41%，而对于Zener 模型，剪切弹性μ1、μ2和剪切黏性η 估计偏差的平均值分别为3.76%、6.89%和4.63%. 从图10 (b)可见，Zener 模型中μ2受表面波速度影响相对较大，但该参数在软组织定征中的作用仍有待研究. 综上可见，黏弹性估计偏差并不是很大，与理论值较为接近.

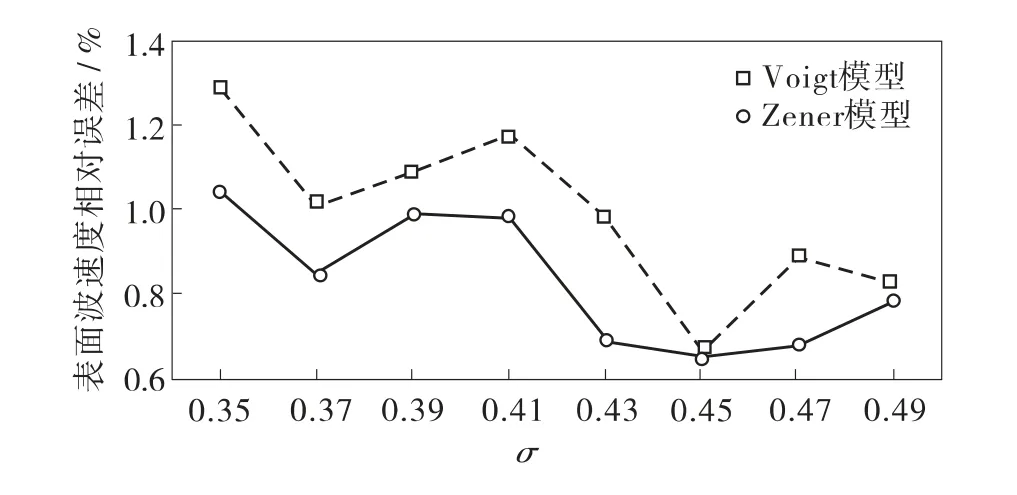
图9 不同泊松比情况下的表面波速度估计偏差Fig.9 Estimate bias of surface wave velocity for different Poisson ratio values

图10 不同泊松比情况下的黏弹性参数估计偏差Fig.10 Estimate bias of viscoelastic parameter for different Poisson ratio values

结 语

本研究提出一种基于表面波的组织黏弹性参数测量方法，推导了Zener 模型表面波速度与黏弹性参数关系式，采用有限元仿真方法分别对Voigt 模型与Zener 模型进行仿真，仿真结果与理论参考值较接近. 该测量法可为进一步实验研究提供参考.

/ References:

［1］Sarvazyan A P，Rudenko O V，Swanson S D，et al.Shear wave elasticity imaging:a new ultrasonic technology of medical diagnostics ［J］. Ultrasound in Medicine and Biology，1998，24(9):1419-1435.

［2］Zhu Ying，Shen Yuanyuan，Chen Xin，et al. Rheological properties analysis of rats liver in fibrosis stages ［J］.Journal of Shenzhen University Science and Engineering，2013，30(2):216-220.(in Chinese)朱 颖，沈圆圆，陈 昕，等. 大鼠肝纤维化分期的流变特性分析［J］. 深圳大学学报理工版. 2013，30(2):216-220.

［3］Rivaz H，Boctor E M，Choti M A，et al. Real-time regularized ultrasound elastography ［J］. IEEE Transactions on Medical Imaging，2011，30(4):928-945.

［4］Ophir J，Alam S K，Garra B，et al. Elastography:ultrasonic estimation and imaging of the elastic properties of tissues ［C］ // Proceedings of the Institution of Mechanical Engineers Part H:Journal of Engineering in Medicine，1999，213(3):203-233.

［5］Lubinski M A，Emelianov S Y，O'Donnell M. Speckle tracking methods for ultrasonic elasticity imaging using short-time correlation ［J］. IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，1999，46(1):82-96.

［6］O'Donnell M，Skovoroda A R，Shapo B M，et al. Internal displacement and strain imaging using ultrasounic speckle tracking ［J］. IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，1994，41(3):314-325.

［7］Nightingale K，Soo M S，Palmeri M，et al. Imaging tissue mechanical properties using impulsive acoustic radiation force ［C］// IEEE International Symposium on Biomedical Imaging:Nano to Macro. ［s.l. ］:IEEE Press，2004，1:41-44.

［8］Nightingale K R，Palmeri M L，Nightingale R W，et al.On the feasibility of remote palpation using acoustic radiation force ［J］. Journal of the Acoustical Society of America，2001，110(1):625-634.

［9］Greenleaf J F，Urban M W，Chen S G. Measurement of tissue mechanical properties with shear wave dispersion ultrasound vibrometry (sduv) ［C］// Embc:Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Minneapolis (USA):［s.n. ］，2009:4411-4414.

［10］Chen S G，Urban M W，Pislaru C，et al. Shearwave dispersion ultrasound vibrometry (sduv)for measuring tissue elasticity and viscosity ［J］. IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，2009，56(1):55-62.

［11］Oestreicher H L. Field and impedance of an oscillating sphere in a viscoelastic medium with an application to biophysics ［J］. Journal of the Acoustical Society of America，1951，23(11):707-714.

［12］ Roylance D. Engineering Viscoelasticity ［DB/OL］.［2001-10-04］. http:// ocw. mit. edu/courses/materialssci-ence-and-engineering/3-11-mechanics-of-materialsfall-1999/modules/visco.pdf.

［13］Miller G F，Pursey H. The field and radiation impedance of mechanical radiators on the free surface of a semiinfinite isotropic solid ［J］. Proceedings of the Royal Society of London Series A:Mathematical Physical and Engineering Sciences，1954，223(1155):521-541.

［14］Pinton G F，Dahl J J，Trahey G E. Rapid tracking of small displacements with ultrasound ［J］. IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，2006，53(6):1103-1117.

［15］Hasegawa H，Kanai H. Improving accuracy in estimation of artery-wall displacement by referring to center frequency of RF echo ［J］. IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，2006，53(1):52-63.

［16］Zheng Y，Chen S G，Tan W，et al. Detection of tissue harmonic motion induced by ultrasonic radiation force using pulse-echo ultrasound and kalman filter ［J］. IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，2007，54(2):290-300.

［17］Christensen R M. Theory of Viscoelasticity ［M］. New York:Dover Publications Inc，2010.

［18］Jensen J A. Simulation of advanced ultrasound systems using Field II ［C］// IEEE International Symposium on Biomedical Imaging:Macro To Nano. Arlington (USA):IEEE Press，2004，1:636-639.