致密岩石变形破坏过程中渗透率演化的试验研究

2013-12-23徐卫亚贾朝军

三峡大学学报(自然科学版) 2013年2期

王欣徐卫亚贾朝军

（1.河海大学岩土工程科学研究所，南京 210098；2.河海大学岩土力学与堤坝工程教育部重点实验室，南京 210098）

自Biot［1］提出了有效应力与渗流场之间关系以来，各国的学者在岩石渗流场与应力场的耦合研究中取得了不少的成果.近年来以中高渗透性介质为对象开展流固耦合渗流研究的较多，针对渗透率低于10－17m2的致密岩石研究则很少.由于岩体成因的多样性，不同岩体的渗流场特征及物理化学特性差别十分显著，使得试验研究成为了研究岩石渗流应力耦合研究的基础方法，对于低渗透率岩石也是如此.

荷载引起渗透率变化是岩石应力渗流耦合研究的一个重要内容.国内外学者对岩石在全应力－应变过程中渗透规律的演化已进行了比较广泛和深入地探讨.岩石变形引起的渗透率变化也已有完整的基于细观机制上的解释.Brace［2］通过对花岗岩进行高压状态下的渗透性试验得出花岗岩的渗透性随着有效围压、围压与孔隙压差的增加而减小.Bieniawski（1967）和Paterson（1978）［3－4］将应力－应变全过程划分为5个阶段.李世平等［5］用多种数学方法对实验数据进行拟合，得到砂岩全应力－应变过程对应的渗透率－应变方程.朱珍德等［6］取花岗岩与灰岩试样分别进行不同围压条件下全应力－应变过程渗流试验，指出岩石脆性岩石破坏前后不同变形阶段的渗流特性.彭苏萍等［7］试验分析了砂岩在全应力－应变过程中渗透率的变化规律，和不同围压下岩石的孔渗性与其所承受的有效侧压大小关系.王环玲等［8］对灰岩和砂岩进行了应力－应变全过程渗透性试验，研究了岩样变形和破坏过程中的轴向应变与渗透率之间的关系，分析了岩样环向应变对渗透率的影响规律.发现渗透率－环向应变曲线与渗透率－轴向应变曲线有相同的变化趋势，但岩石环向变形比轴向变形更能灵敏地反映渗透率的演化规律.姜振泉等［9－10］根据伺服试验获得的渗透率－应变关系与应力－应变关系提出临界抗渗强度和起始抗渗强度两个特征值，建立了峰值应力前岩石渗透性－应力关系数学表达式.

此外，国内外众多学者通过不同的实验装置和实验方法研究了岩石渗透性和应力之间的关系并总结出了岩石渗透率与应力之间的经验公式［11－14］.由于试验仪器以及试验方法的限制，大部分研究都集中在砂岩等高渗透性的软岩上，对致密脆性岩石的研究鲜有报道，另外，不同学者得出的结论与实际相差很大，为工程的应用带来极大的困难.

本文通过最新研制的自适应全自动岩石三轴试验机，对致密脆性的花岗片麻岩开展了相同围压不同孔隙压力下的渗透性试验，探讨了应力和渗压等与渗透率的关系，为工程中渗流应力耦合问题提供参考.

1 试验原理及方法

对渗流应力耦合的研究概况起来有3种方法：1）以物理模型为基础，利用数值方法建立耦合关系；2）直接通过渗透性试验，总结渗透率与应力或者应变的关系；3）通过渗透性试验，假设一定的函数关系，利用数学方法推导确定变量的关系.可见试验对于渗流应力耦合研究的重要性.由于岩石渗透性试验压力较高，试样密封性要好，同时对渗透率测量精度有较高的要求，国内能做此类试验的仪器并不多.

1.1 试验原理

应力渗流耦合试验在自适应全自动岩石三轴试验机上进行，该系统由河海大学与法国国家科研中心（CNRS）、法国里尔科技大学（USTL）共同研制而成，可进行静水压缩、三轴排水压缩、三轴不排水压缩、渗透试验、流变试验等试验；可实现全程计算机控制与分析，保证试验控制与数据采集的实时和准确.渗流应力耦合试验原理如图1所示.

图1 渗透性试验原理示意图

其中，σ1为轴向压力，σ3为围压，p1为试样上端水压，p2为下端水压，岩石试样上下两端各有一块透水钢板，能使水压均匀地作用于整个试样端面.在渗透试验过程中，先施加一定的轴压σ1，围压σ3，在岩样两端施加孔隙水压p1＝p2＝p0，然后利用孔隙压力系统在岩样两端形成孔隙压力差Δp，从而水流通过试样发生渗流，在试验中为了保证水不从橡胶套与岩样之间流动，始终保持p1＜σ3.

本试验过程中的数据采集由计算机自动控制，每施加一级轴向应力，可以采集到试样轴向变形、环向变形以及水压泵随时间的变化过程，因此可以依据所记录的应变以及渗透性数据，得到应力－应变和渗透性－应变关系.

根据计算机自动采集的数据，根据darcy定律可以计算渗透率

式中，k为岩石的渗透率（darcy）；μ 为水的粘度；Q 为流量；L 为试样的长度；A 为试样截面面积；Δp 为两端水压差.

1.2 试验设备与方法

试样为取自青岛某大型地下工程的晚元古界花岗片麻岩，浅肉红色，主要矿物成分为钾长石、斜长石、石英、角闪石、黑云母等，中细粒花岗结构，块状构造，岩体完整.编号分别为QDA－1，QDA－2，QDA－3.编号为QDA－1的试样具有明显的纵向裂隙，QDA－1，QDA－2比较完整.所有的试样都在相同的围压条件下进行渗透试验，试验所控制的参数：围压4.0MPa，孔隙压力分别为1.0MPa，2.0MPa，3.0MPa.

2 试验结果与分析

2.1 试验结果

本文对花岗片麻岩试样进行渗透特性试验，试验条件及试验结果见表1.

表1 试样渗透率特征

2.2 渗透规律

根据计算机采集的数据计算出渗透率，由试验所得数据做出图2所示应变－渗透率曲线.

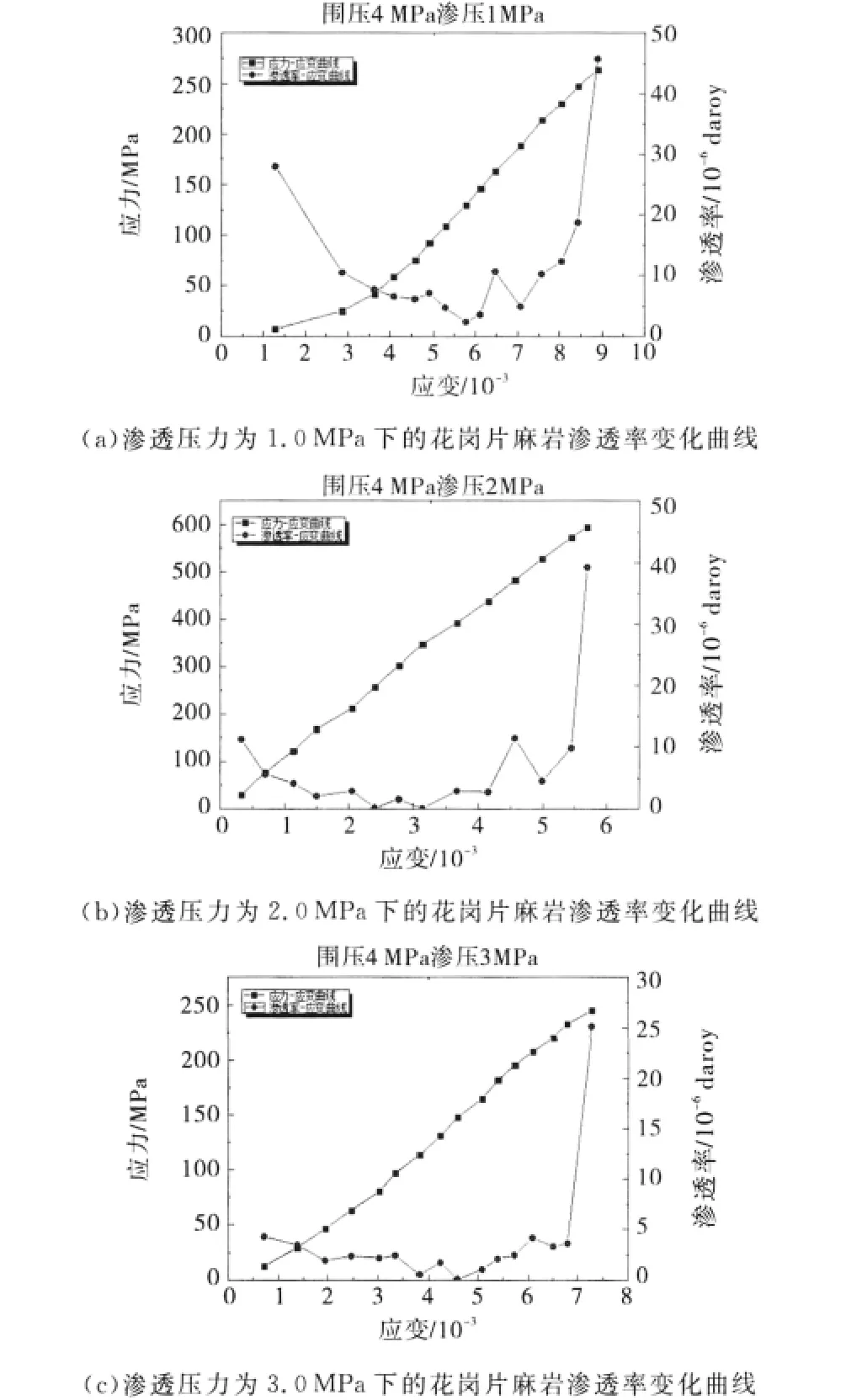
图2 不同渗透压力下的花岗片麻岩渗透率变化曲线

由图2的应力－应变关系可以看出，花岗片麻岩应力与应变的关系是一近似直线，直到试样发生破坏为止，塑性阶段不明显，因此花岗片麻岩为一种脆性岩石.在4MPa围压下，不同渗压的试样渗透规律大致相同，在应力加载初级阶段，渗透率随着应变的增加而缓慢降低.这主要是由于岩石在结构上是复杂的不连续体，存在孔隙和原生微裂隙，对岩样施加应力，使得裂隙压密闭和，阻塞了渗流通道，试样渗透率降低.在弹性工作阶段，随着轴向应力的增加，岩样发生弹性变形，在荷载和孔隙压力的共同作用下，孔隙和裂隙进一步被压密，使得渗透率进一步降低，并达到最低点.随着应力的增加，轴向应变继续增大，试样进入屈服变形阶段，此时岩石内部萌生微裂隙，原生的微裂纹进一步发生扩展，为渗流提供了通道，因此渗透率开始增加.继续加载，致使试样发生变形破坏，微裂纹和微裂隙演化为宏观裂隙，渗透率达到峰值.

2.3 不同渗压下应变－渗透率关系

由表1 可以看出，当渗压分别为1.0，2.0，3.0 MPa时，岩样的最大渗透率分别为45.74，25.12，39.19darcy，而最小渗透率分别为2.37，0.08，0.02 darcy，为了更直观地对比，对破坏前的岩样的渗透率取平均值，大小分别为9.55，4.55，2.37darcy.如图3所示，对于不同渗压的岩样，其渗透率表现出很大的离散性，这主要是由于岩石是一种多相的不连续介质，渗流能力不仅与围压、轴向压力、孔隙压力等有关，与岩石中的裂隙、孔隙的发育情况有直接关系.

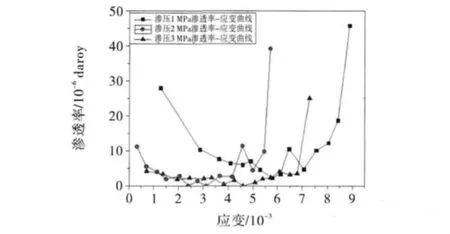
图3 渗透率－轴向应变关系曲线

试验表明，不同裂隙发育状况的岩石的渗透率并不随渗压的增加而增加，由图4可以看出，QDA－1岩样具有明显竖向发育裂隙，而QDA－2，QDA－3岩性比较完整，因而即使在较低渗透压力下，依然具有较大的渗透率.

图4 试样图片

2.4 致密脆性岩石变形破坏过程中渗透率演化

岩石是一种含有孔隙和裂隙的高度非均匀材料，在应力作用下发生渗流是一个动态的演化过程，渗流场的改变会引起应力场的变化，应力场的改变同时会对渗流场产生影响.

应力－轴向应变，渗透率－轴向应变关系曲线表明，直接耦合效应很明显.首先，当发生应力扰动时，岩体孔隙和裂隙中的水的平衡被打破，渗透压力改变的同时，缝隙中水的质量发生改变，其次，孔隙水压力和孔隙水质量的变化将引起岩体体积的变化和结构的改变.同时针对致密脆性岩石，仔细比较图2可以看出，在应力加载后期，未发生屈服破坏之前，渗透率都有一个“突跳”现象.本文研究认为主要是由于致密脆性花岗片麻岩本身微观尺度上的性质所致，岩石是一种含有孔隙、微裂隙等各种类型毛细管的多孔介质，其中有一部分孔隙空间相互连通，流体可以在其中流动，称为有效孔隙；而不连通的孔隙空间或虽然连通但属死端孔隙的这部分空间是无效孔隙空间［15］.在受力作用下，有效孔隙和无效孔隙体积都发生闭和，则渗透率开始减小，当有效孔隙闭和到最小值时，渗透率也降到最低；进一步受力，孔隙发生滑移，原生的无效孔隙集结在一起演化为大的有效孔隙，在该状态下，渗透率会有一个突然增大，随着进一步的加载，原先演化的有效孔隙再次滑移而使得渗透率降低，此结论有待对花岗片麻岩细观尺度的力学特性进一步的研究.

3 结论

1）试验所获得的应力－应变和渗透率－应变曲线表明应力加载过程中，经历了孔隙和裂隙的压密－弹性变形－屈服破坏阶段，每一个阶段渗透率的变化规律都不相同.压密阶段，随着原生裂隙的闭和，渗透率降低；弹性阶段，岩石发生弹性变形，孔隙和裂隙进一步压密，渗透率进一步降低直至最低点；随着轴向应力的增加，岩石在外荷载和孔隙压力的共同作用下，内部结构开始出现微裂隙萌生和原始孔隙的扩展并演变成宏观裂纹，最终岩石发生破裂，渗透率也在此过程中增加.

2）致密脆性花岗片麻岩主要发生裂隙渗流，不同的孔隙压力对岩石的渗透性产生影响.理论上，孔隙压力越大，渗透率越大.但是试验表明，岩石的渗透率不仅与外界的围压、渗透压力、轴向压力有关，同时岩石本身结构的完整性对渗透率也会产生影响.当孔隙压力不大时，裂隙的发育程度与孔隙压力相比对渗流占主导作用，裂隙发育程度越高，即使渗透压力较小的情况下，渗透性也越高.

3）环向应变也可以反应岩石变形破坏整个过程中的渗透率的演化规律，从试验结果看出，环向应变比轴向应变更能体现岩石发生软化屈服破坏的过程；同时发生相同的渗透率变化时，环向变形响应更加灵敏.因此为渗流应力耦合提供了一个新的角度.

4）由应力－轴向应变和渗透率－轴向应变总结致密脆性的花岗片麻岩的渗流应力耦合机理，发生直接耦合效应很明显；发生屈服破坏之前的渗透率“突跳”现象的研究表明，其与岩石的微观性质有关，岩石内部的孔隙分为有效孔隙和无效孔隙，在应力作用下会发生孔隙的滑移，在此应力加载阶段，原生的无效孔隙集结在一起演化为大的有效孔隙会导致渗透率的突然增加.在大型地下工程渗流应力耦合长期稳定性的研究当中，为大型洞室在应力作用下发生渗流破坏提供参考.

［1］ Boit M A.General Theory of Three－dimensional Consolidation［J］.Journal of Applied Physics，1941，12：155－164.

［2］ Brace W F，Walsh J B，Frangos W T.Permeability of Granite under High Pressure［J］.Journal of geophysical research－atmospheres，1968，73（6）：2225－2236.

［3］ Makurat A，Barton N，Rad Ns.Joint Conductivity Variation Due to Normal and Shear Deformation Rock Joints［M］.Balkema：Rotterdam，1990.

［4］ Bieniawski Zt.Mechanism of Brittle Fracture of Rock［J］.International Journal of Rock Mechanics ＆ Mining Sciences，1967，4（4）：407－423.

［5］李世平，李玉寿.岩石全应力－应变过程对应的渗透率－应变方程［J］.岩土工程学报，1995，17（2）：13～19.

［6］朱珍德，张爱军，徐卫亚.脆性岩石全应力－应变过程渗流特性试验研究［J］.岩土力学，2002，23（5）：555－560.

［7］彭苏萍，孟召平，王虎，等.不同围压下砂岩孔渗规律试验研究［J］.岩石力学与工程学报，2003，22（5）：742－746.

［8］王环玲，徐卫亚，杨圣奇.岩石变形破坏过程中渗透率演化规律的试验研究［J］.岩土力学，2006，27（10）：1703－1709.

［9］姜振泉，季梁军，左如松，等.岩石在伺服条件下的渗透性与应变、应力的关联性特征［J］.岩石力学与工程学报，2002，21（10）：1442－1446.

［10］姜振泉，季梁军.岩石全应力－应变过程渗透性试验研究［J］.岩土工程学报，2001，23（2）：153－156.

［11］Louis C.Rock Hydroulies.In：Rock Meehanies，Ed.byLMuller，1974.

［12］Snow D T.Rock Fracture Spacings.Openings and Porosities［J］.1968，94（SM1）：73－91.