覆冰输电线路舞动的非线性数值分析

杨 伦，楼文娟，潘小涛

浙江大学结构工程研究所，杭州310058

舞动是输电导线在恶劣风雨雪冰冻气候条件下产生的大幅低频振动，会对输电塔线造成构件及电气方面的损坏，危害电网的安全和电力的正常供应［1-2］.

自Den Hartog［3］和Nigol 等［4］分别提出竖向和扭转舞动机理以来，不少学者针对覆冰导线提出了各种二自由度［5-6］和三自由度耦合舞动质点模型［7-8］，并采用摄动法、多尺度法等近似解析的方式求解了舞动响应. 然而鉴于质点舞动模型无法考虑导线大幅振动所致的几何非线性效应，Luongo［9］、Liu［10］和Yan［11］等建立了二维或三维连续体耦合非线性模型，并针对导线在初始条件下的舞动稳定性、分岔特征以及内共振模式展开了一系列的定性分析. 值得注意的是，以上连续体舞动模型仍然过于简化，忽略了实际大气环境下线路不均匀覆冰、几何刚度时变特征、不同阶振型之间的耦合效应以及不同档距导线之间的相互作用等因素的影响，不能有效反映输电线路舞动响应的动态物理特征. 为此，Desai 等［12］针对覆冰导线舞动的非线性特征，提出了三节点抛物线索单元，并建立了用于单导线舞动分析的非线性有限元法. 与商业有限元软件提供的索单元不同的是，Desai 提出的索单元具有扭转自由度，同时能考虑偏心覆冰对舞动的影响. 李黎等［13］利用具有扭转自由度的二节点索单元，并通过将分裂导线等效为单导线的方式，建立了连续多档距覆冰导线有限元模型. 然而有关研究表明，将分裂导线等效为单根导线无法考虑子导线之间的尾流干扰效应，从而导致得出的舞动幅值偏小［14］. 因此，刘小会等［15］基于Desai 提出的三节点抛物线索单元，采用对索节点扭转自由度扩充为3 个方向上转动自由度的方式，建立了能够对各子导线施加不同气动荷载，且考虑间隔棒与子导线运动耦合效应的分裂导线有限元模型.

值得注意的是，覆冰分裂导线的扭转刚度远大于单导线，致使两者在起舞机理方面有着显著差别. 为此，本研究基于完全拉格朗日格式(Total Lagrange)，建立适用于单导线和分裂导线舞动数值模拟的非线性有限元动力分析方法，采用具有扭转自由度的三节点抛物线索单元离散覆冰单导线. 对于覆冰分裂导线，在单导线有限元法的基础上，利用欧拉梁单元模拟间隔棒的运动过程. 为尽可能地提高计算效率，提出梁单元转动自由度缩聚法实现间隔棒与分裂子导线之间的耦合，并运用随转坐标系法求解舞动过程中的梁节点不平衡力. 在此基础上，结合覆冰导线气动力系数的风洞试验结果，分别考察覆冰单导线和四分裂导线在湍流和均匀流场中的起舞机理和舞动响应特征之异同.

1 覆冰导线有限元法

1.1 单导线的动力平衡方程和气动荷载

基于完全拉格朗日格式，具有扭转自由度的三节点抛物线索单元描述导线单元的非线性动力平衡方程［12］为

如图1 所示，作用于覆冰导线某截面的气动荷载可表示为

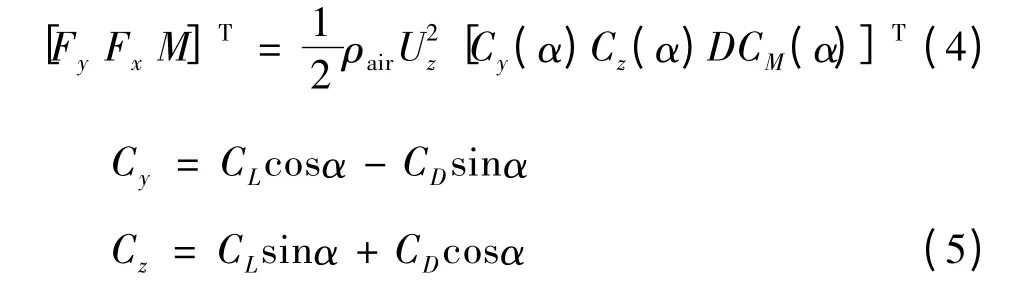
其中，Fx、Fy和M 分别为x 向、y 向和扭转向的节点气动荷载;ρair为空气密度;D 为导线直径;Uz为来流风速;CL、CD和CM分别是导线截面的升力系数、阻力系数和扭转系数，与导线覆冰形状和风对导线的攻角α 有关，

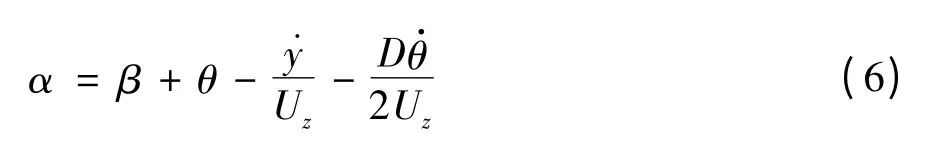
其中，˙y 为竖向运动速度;β 和θ 分别为初始风攻角和t 时刻导线的扭转角. 式(6)右第3 和第4 项分别代表导线竖向和扭转运动速度对总风攻角的影响.

图1 覆冰导线截面风攻角及受力Fig.1 Attack angle and aerodynamic force of iced conductor

1.2 覆冰分裂导线有限元模型

分裂导线由多根单导线和间隔棒共同组成. 间隔棒的作用在于保持子导线间距，防止子导线之间由于电磁吸引以及风力而引发的相互靠近和碰撞鞭击. 同时，受间隔棒约束作用的影响，分裂导线舞动时表现为显著的整体运动. 因此从数值模拟的角度来看，只需对按照一定规律排列的多根子导线构成的振动系统中加入模拟间隔棒的梁单元即可. 这一过程中首先需要解决的是如何高效、可靠地实现分裂子导线与间隔棒的连接. 另外，分裂导线发生舞动时间隔棒的运动表现出典型的大转动、小应变特征，精确求解间隔棒在运动过程中的单元不平衡抗力向量，是保证舞动计算收敛性的关键. 本研究分别采用梁单元转动自由度缩聚和随转坐标系法［16］，实现子导线与间隔棒的连接，并求解梁单元节点的不平衡抗力向量.

1.2.1 分裂子导线与间隔棒的连接

分裂导线由单导线和间隔棒组成，其有限元模型如图2 所示. 各子导线之间通过由欧拉梁单元模拟的间隔棒相连，其中梁单元节点有3 个平动自由度及3 个扭转自由度，子导线单元节点有3 个平动自由度和1 个转动自由度.

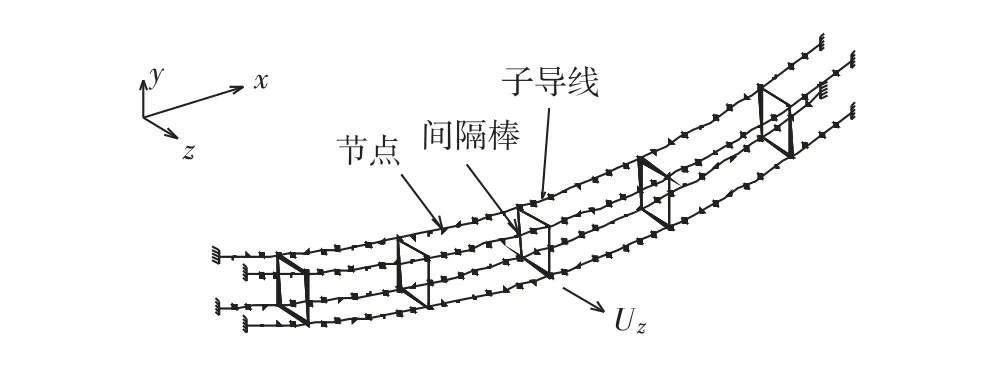
图2 分裂导线有限元模型Fig.2 Finite element model of bundled conductors

针对分裂子导线与间隔棒的连接问题，文献［15］提出一种对索单元节点扭转自由度扩张的方式来模拟子导线与间隔棒的连接. 即在间隔棒与子导线的交点处，将索节点扭转自由度投影至梁节点3个方向的转动自由度上，交点处索节点自由度数由4 个增加至6 个. 采用该连接方式会在一定程度上增加整个系统的自由度数，从而影响求解效率.

为尽可能地减小计算量，提高舞动分析效率，本研究采用对梁节点扭转自由度缩聚的方法实现梁单元节点与索单元节点的耦合. 在间隔棒与子导线的连接处，保持索单元节点的4 个自由度不变，将梁单元节点在整体坐标系下的3 个转动自由度缩聚为1 个沿索单元轴线方向的扭转自由度. 以导线初始构型为参考构型，t 时刻梁单元在整体坐标系下的节点位移向量可表示为

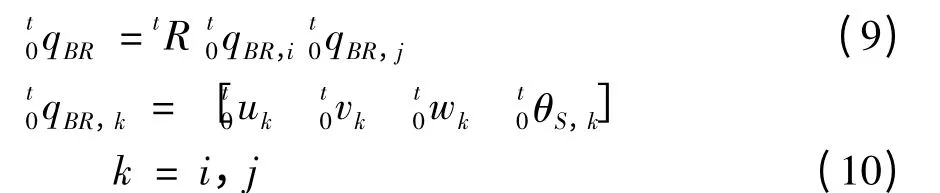
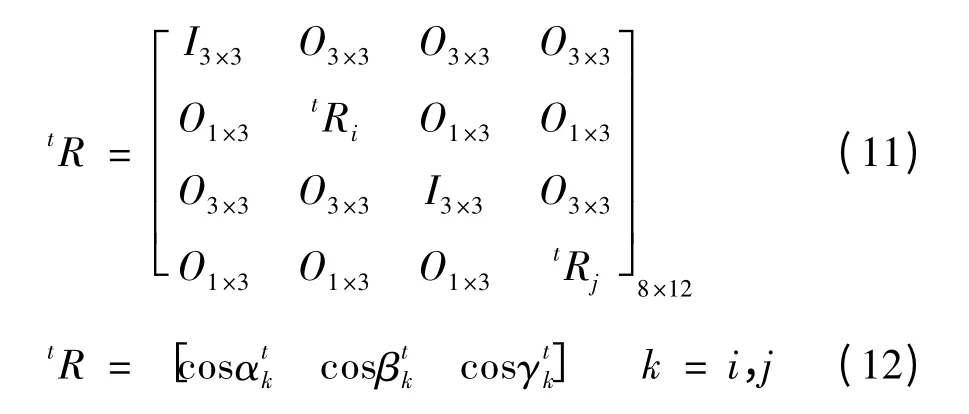
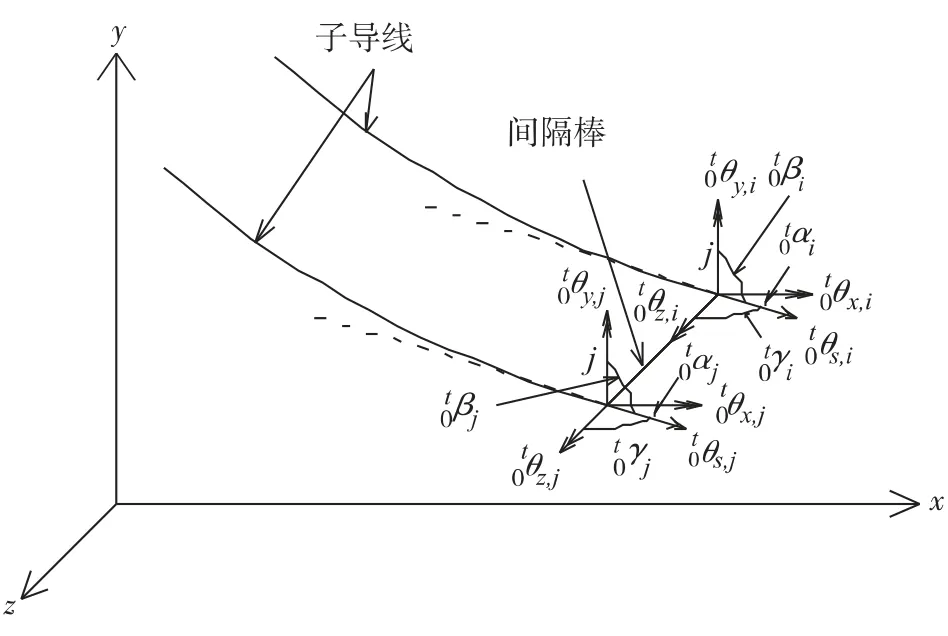
图3 分裂子导线与间隔棒的连接Fig.3 Connection between sub-conductor and space rod

1.2.2 梁单元节点抗力的计算

分裂导线舞动过程中，间隔棒的节点位移可分解为刚体运动和单元变形两部分. 传统的完全拉格朗日列式法仅适用于转动较小的情形，转动位移较大时无法有效分离单元的刚体转动和单元变形，导致在结构非线性增量求解过程中无法精确计算由于纯变形产生的单元抗力. 为此，本研究运用随转坐标系方法［16］解决问题. 如图4，选定t = 0 时刻梁单元构型所在的局部坐标系为初始坐标系，则t 时刻梁单元节点在初始坐标系下的位移向量可表示为

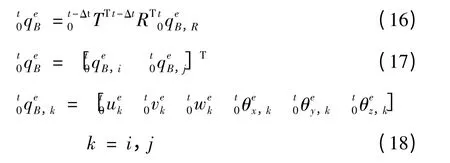
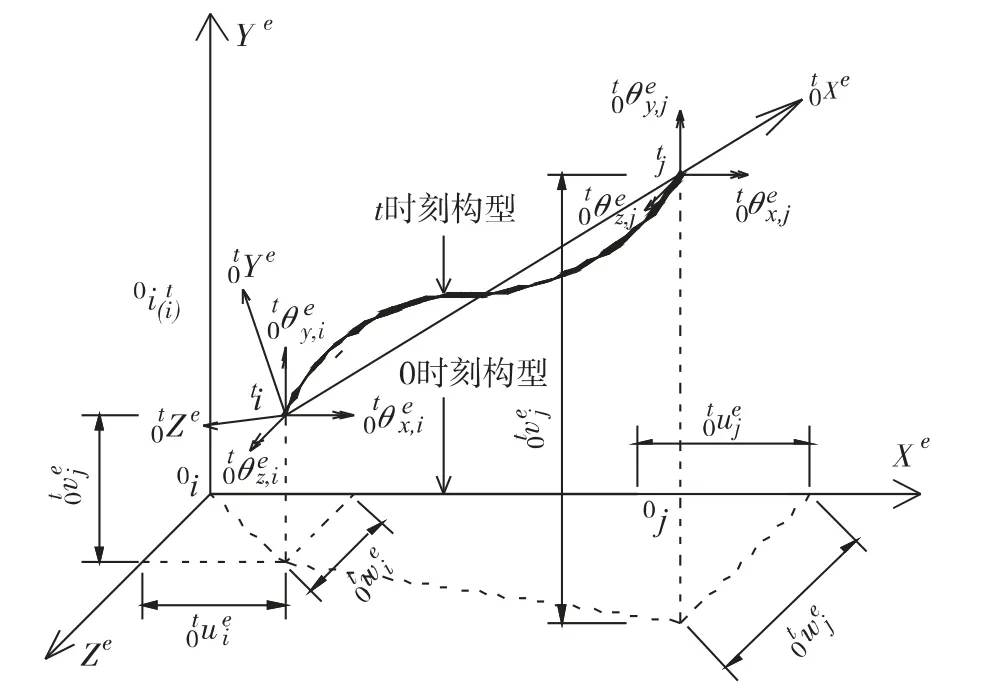
图4 梁单元不同时刻的构型Fig.4 Configurations of beam element at different time

在初始局部坐标系下梁单元两端平动位移增量可表示为

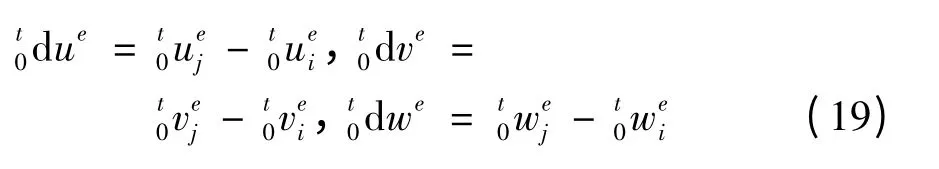
由于梁单元在运动过程中变形较小，因此在t 时刻的弦长Lt可表示为

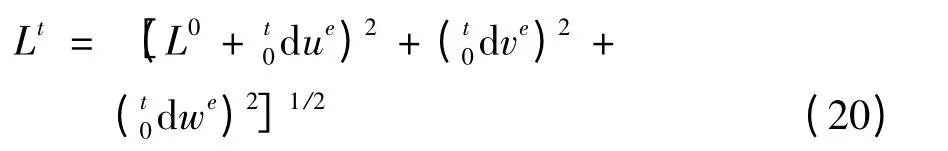
则梁单元的伸长量ΔLt为

如图5，将梁单元在t 时刻局部坐标系的坐标原点移至初始时刻局部坐标系的坐标原点，则转动刚体位移可用梁端位移平动位移增量和扭转角表示为

梁节点在t 时刻局部坐标系下的转动变形位移为

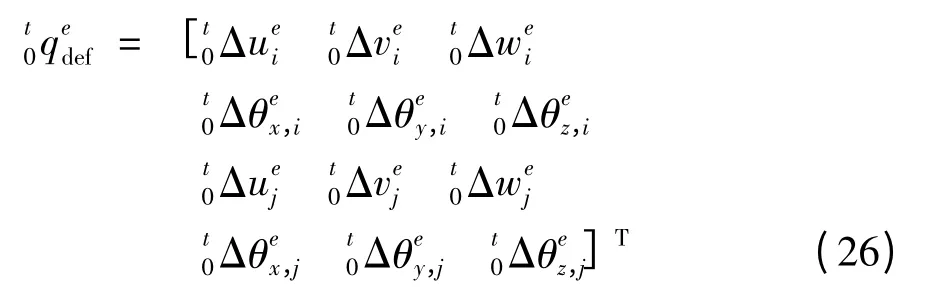
将梁单元在局部坐标系下的单元抗力转换至整体坐标系下，并进行自由度缩聚，可得梁单元在整体坐标系下的节点抗力为

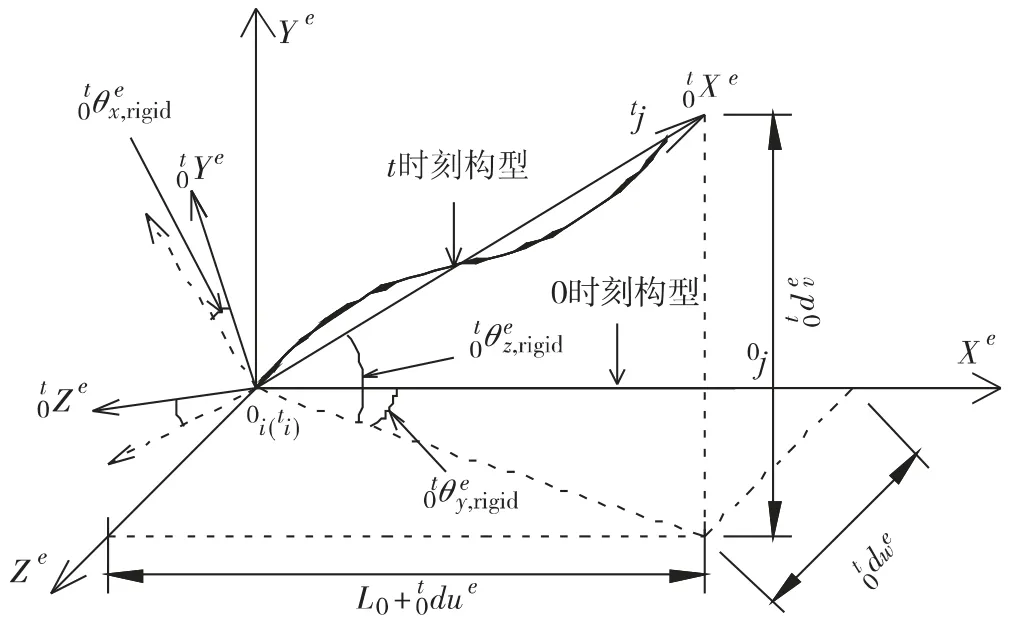
图5 梁单元转动刚体位移Fig.5 Rigid rotational displacement of beam element

1.3 非线性动力方程的求解

求得表征子导线和间隔棒舞动特性的单元矩阵和荷载向量后，便可根据单元定位向量获得单导线或者分裂导线系统的非线性运动方程. 本研究采用无条件稳定的Newmark 法对方程直接积分求解，并运用Newton-Raphson 法对每个时间步末尾的位移向量进行迭代求解. Newmark 法采用平均加速度方案，即积分精度参数α 和稳定性参数β 分别取0.25和0.5. 那么t 至t +Δt 过程中，基于完全拉格朗日格式的递推迭代公式可表示为［18］

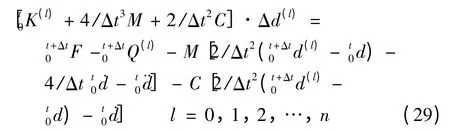
2 有限元算例验证

为验证本研究计算分裂导线方法的有效性，以某工程的单跨四分裂导线为例，采用本研究方法和ANSYS 有限元软件求解导线舞动响应. 分裂导线等间距设置5 组间隔棒，子导线物理参数如表1.

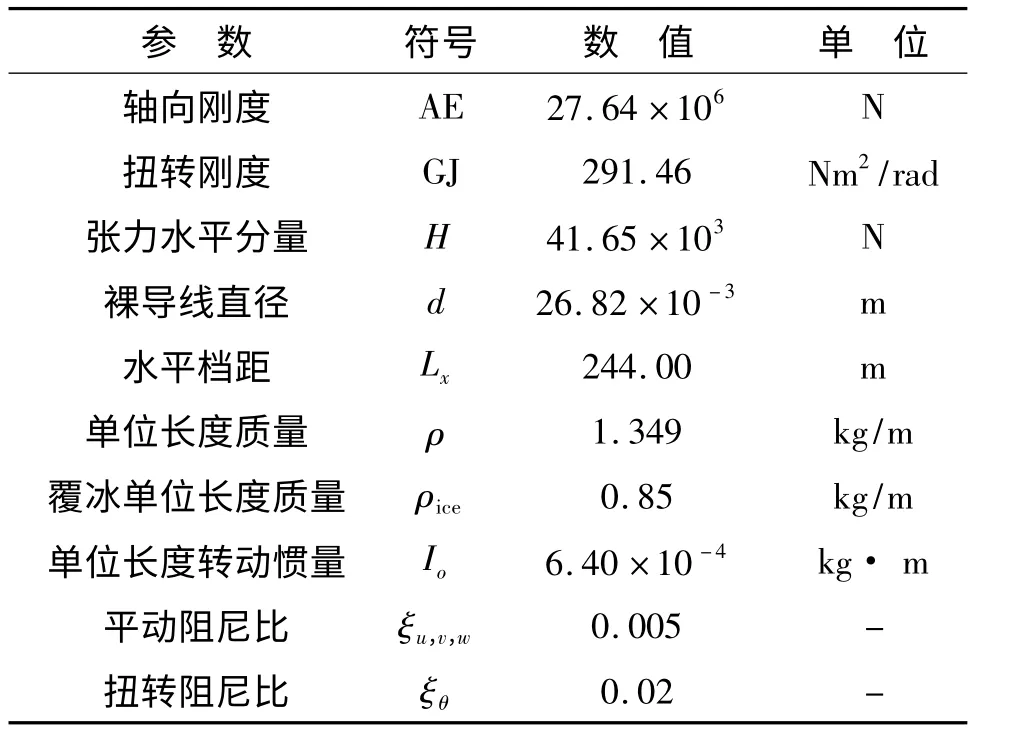
表1 覆冰导线物理参数Table 1 Physical parameters of iced conductor

ANSYS 模型中分别采用Link 10 单元和Beam 4单元离散子导线和间隔棒. 由于分裂导线的整体抗扭刚度比子导线绕自身轴的抗扭刚度大得多，因此在ANSYS 模型中不考虑子导线的抗扭刚度. 本研究计算模型中，每根子导线划分20 个三节点抛物线索单元. 鉴于Link 10 单元是2 节点单元，为保证两种方法的节点数量保持一致，ANSYS 计算模型中每根子导线划分40 个单元.

分别在每根子导线跨中节点上同时施加400 N、400 N 和40 N·m 的垂直、水平和扭转向突加荷载.经计算，两种方法所得的子导线跨中位移时间历程如图6. 不难看出，两种方法得出的计算结果吻合很好，说明本算法可靠有效.

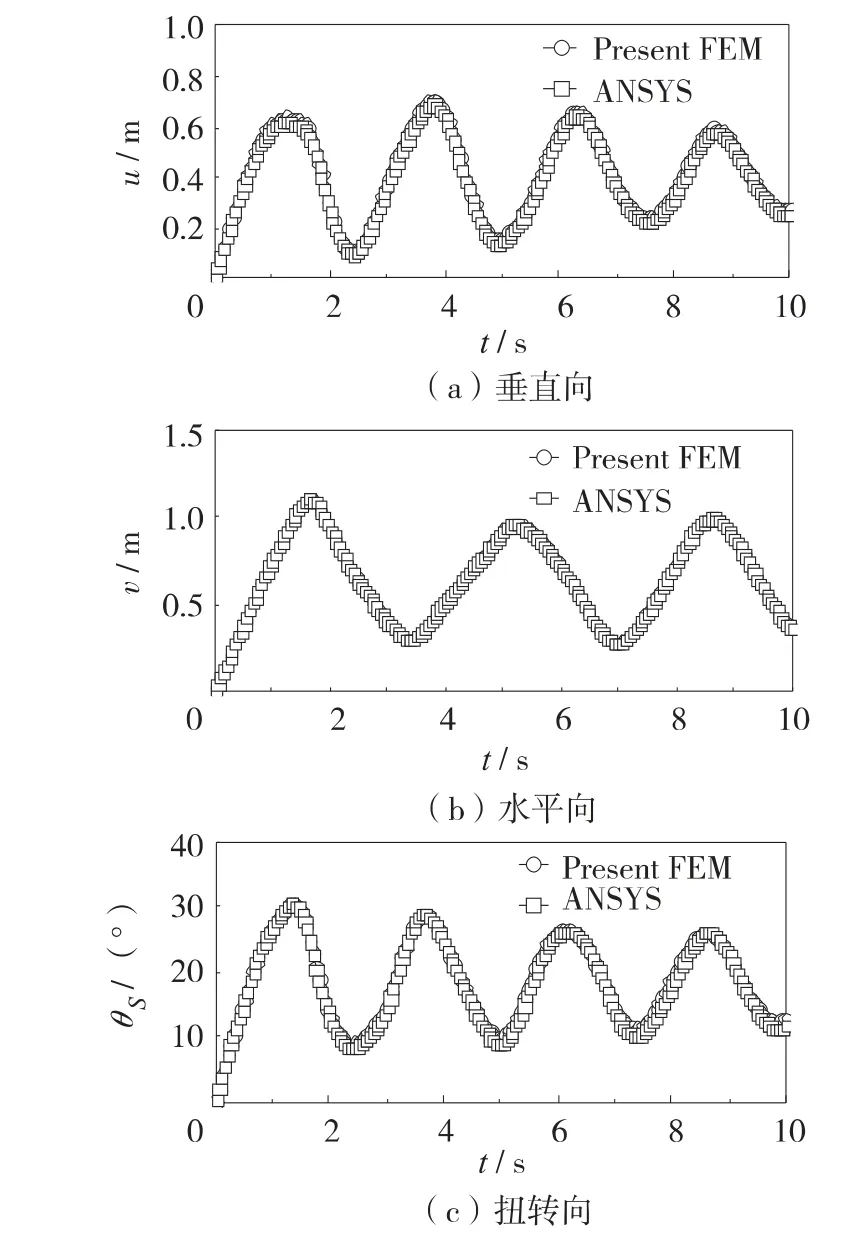
图6 子导线跨中位移时程Fig.6 Time histories of displacement of sub-conductor at the mid-span

3 覆冰导线舞动数值模拟

3.1 覆冰导线气动力

以新月形覆冰为例，制作1∶1 四分裂导线节段模型，模型长度为1.0 m. 鉴于舞动发生时的风速大多低于20 m/s，本研究试验风速取为15 m/s. 利用高频动态测力天平，考察导线在均匀流和6%均匀湍流场下新月形覆冰四分裂导线整体气动三分力系数随攻角的变化规律(如图7).

图7 覆冰导线气动三分力系数随风攻角的变化规律Fig.7 Aerodynamic coefficients of iced conductor versus wind attack angle

由于Den Hartog 系数和Nigol 系数分别体现了覆冰导线的竖向和扭转稳定性，因此结合气动力测试结果，给出了以上2 类系数随初始攻角的变化规律(如图8). 不难看出，初始攻角落在25°和175°附近时两类系数均小于零，说明在此情形下导线极有可能丧失稳定性.

3.2 覆冰导线舞动响应分析

以表1 导线参数为例，采用本研究提出的有限元法，分别对单根和四分裂导线在均匀流和湍流条件下进行舞动分析. 结合图8 给出的不稳定攻角范围，选取25°和175°为初始风攻角. 鉴于舞动属于典型的自激振动，主要与平均风荷载有关，计算风速取为13 m/s. 另外，为保证算法的收敛性，舞动计算的时间步长取为0.01 s.

3.2.1 覆冰单导线舞动响应分析

图9 为25°攻角下覆冰单导线在2 类流场下的跨中舞动响应. 初始风攻角为25°时，无论在湍流还是均匀流作用下，单导线在垂直方向上均保持稳定. 但在这2 种流场中未发生舞动的原因有着本质区别:在湍流场中，虽然Den Hartog 系数和Nigol系数均为负，但是单导线的抗扭刚度很小，在扭转系不稳定攻角范围内，单导线会发生振幅较大的扭转舞动，使动态攻角极易脱离Den Hartog 系数小于零的区域，所以其竖向振动幅值很小，可认为保持稳定;而流场为均匀流时，Den Hartog 系数和Nigol系数均为正，因此覆冰单导线并未发生舞动.

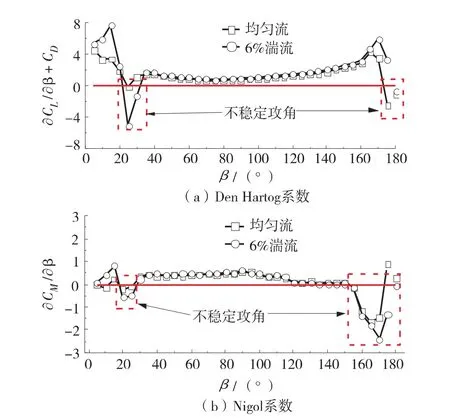
图8 覆冰导线的Den Hartog 系数和Nigol 系数Fig.8 Nigol coefficient of iced conductor

图9 25°风攻角下单导线在两类流场中的跨中舞动响应Fig.9 Galloping responses of mid-point of single conductor with attack angle of 25° in two types of flow field

图10 给出当风向改变、使初始风攻角变为175°时的导线舞动响应. 可见，湍流作用下覆冰单导线仅发生了大振幅的扭转舞动，其机理与湍流场中25°初始风攻角下的舞动机制相同. 当流场为均匀流时，Nigol 系数转变为正而Den Hartog 系数为负，因此单导线发生了振幅较大的竖向舞动. 从图9 (b)和图10 (b)均不难发现，单导线扭转舞动的特征频率更高.

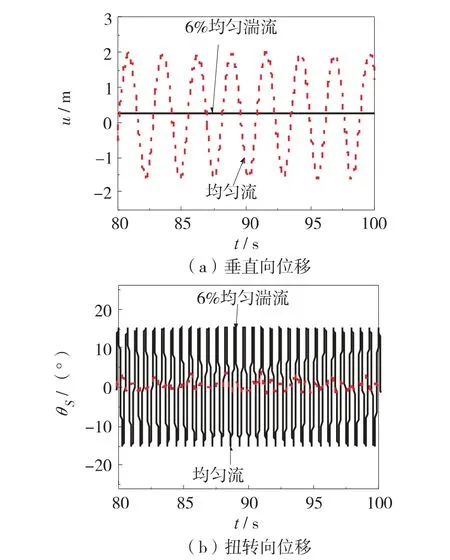
图10 175°风攻角下单导线在两类流场中的跨中舞动响应Fig.10 Galloping responses of mid-point of single conductor with attack angle of 175° in two types of flow field

3.2.2 覆冰四分裂导线舞动响应分析

图11 为25°初始攻角下四分裂导线在两类流场中的跨中舞动响应. 由于分裂导线的扭转刚度较大，因此在湍流场中即使初始攻角落入Nigol 系数的不稳定区域，其扭转向仅发生了小幅振动. 在此情形下，Den Hartog 系数起主导作用，所以分裂导线发生了显著的竖向舞动. 流场为均匀流时，Den Hartog 系数和Nigol 系数均大于零，因此分裂导线竖向和扭转向均保持稳定.

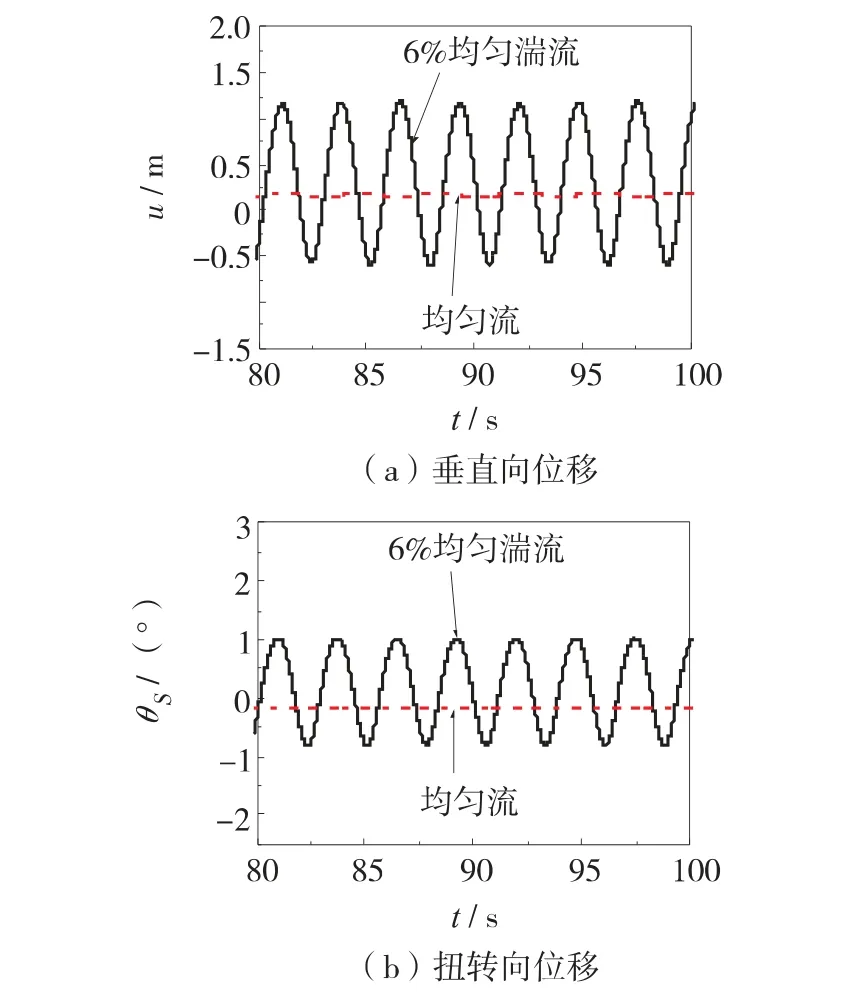
图11 25°风攻角下分裂导线子导线在两类流场中的跨中舞动响应Fig.11 Galloping responses of mid-point of sub-conductor with attack angle of 25° in two types of flow field

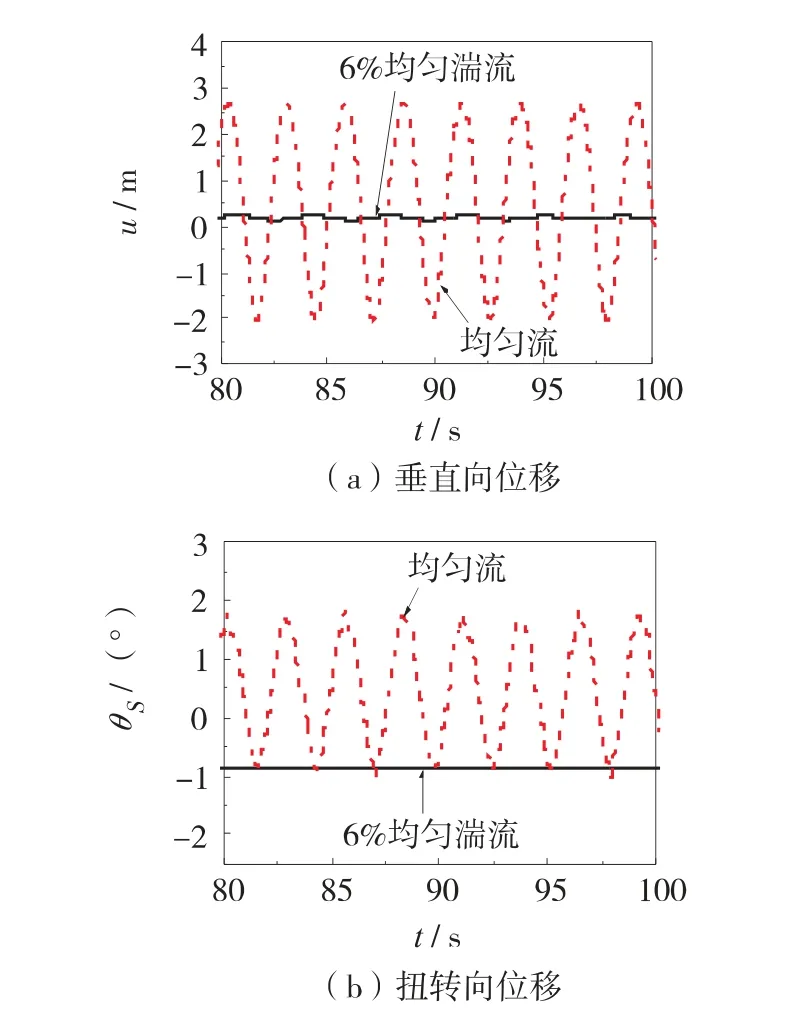
图12 175°风攻角下分裂导线子导线在两类流场中的跨中舞动响应Fig.12 Galloping responses of mid-point of sub-conductor with attack angle of 175° in two types of flow field

图12 给出175°攻角下分裂导线的舞动响应.结合图8 不难看出，在湍流场中，虽然Nigol 系数为负，但由于分裂导线的抗扭刚度较大且Den Hartog 系数大于零，导线并未舞动.然而在均匀流场中，Den Hartog 系数变为负值，因此分裂导线发生了振幅较大的竖向舞动. 同时，受竖向舞动的激励作用，分裂导线在扭转向发生了振幅较小的受迫振动.

结 语

基于完全拉格朗日格式，采用具有扭转自由度的三节点抛物线索单元和欧拉梁单元，分别模拟导线和间隔棒，提出了梁节点自由度缩聚法，实现了子导线和间隔棒的连接，建立了适用于单导线和分裂导线舞动分析的非线性有限元法. 结合覆冰导线在湍流场和均匀流场中的气动力测试结果，求解了新月形覆冰单导线和四分裂导线的舞动响应，并揭示了单导线和分裂导线在不同流场中的起舞机理.研究表明:由于单导线抗扭刚度较小，在Nigol 系数为负的情况下会发生大幅扭转舞动，所以动态攻角极易脱离升力系数的不稳定区域，保证了单导线的竖向稳定性;对于抗扭刚度较大的分裂导线来说，其气动稳定性主要受升力系数的特征控制，即使在Den Hartog 系数和Nigol 系数均为负的情况下，仍易发生大幅的竖向舞动. 下一步笔者将基于D 形覆冰四、六、八分裂导线子导线气动力测试结果，对各子导线施加不同的气动荷载，运用本文给出的非线性有限元算法，细致考察子导线间气流干扰效应对分裂导线舞动特征的影响.

/ References:

［1］Zhu Kuanjun，Fu Dongjie，Wang Jingchao，et al. The galloping and its preventing techniques on overhead transmission line ［J］. Electrical Equipment，2009，9(6):8-12.(in Chinese)朱宽军，付东杰，王景朝，等. 架空输电线路的舞动及防治［J］. 电力设备，2009，9(6):8-12.

［2］Wei Chong，Pan Shaocheng，Tang Minggui，et al. Analysis and threatment of the galloping of 500kV transmission line ［J］. Electric Power Construction，2011，32(4):24-27.(in Chinese)魏 冲，潘少成，唐明贵，等. 500kV 输电线路舞动分析及治理［J］. 电力建设，2011，32(4):24-27.

［3］Den Hartog J P. Transmission line vibration due to sleet［J］. AIEE Transactions，1932，51(4):1074-1086.

［4］Nigol O，Clarke G J，Havard D G. Torsional stability of bundle conductors ［J］. IEEE Transactions on Power Apparatus and Systems，1977，96(5):1666-1674.

［5］Yu P，Popplewell N，Shah A H. Instability trends of inertially coupled galloping ［J］. Journal of Sound and Vibration，1995，183(4):663-678.

［6］Macdonald J H G，Larose G L. Two-degree-of-freedom inclined cable galloping ［J］. Journal of Wind Engineering and Industrial Aerodynamics，2008，96(3):291-326.

［7］Wang J W. Large vibrations of overhead electrical lines:a full 3-dof model for galloping studies ［D］. Province of Liège (Belgum):Universite de Liege，1996，151:1-227.

［8］Chen Xiaoming，Deng Hongzhou，Wang Zhaomin. Conductor galloping stability analysis of long-span transmission system ［J］. Engineering Mechanics，2004，21(1):56-60.(in Chinese)陈晓明，邓洪洲，王肇民. 大跨越输电线路舞动稳定性研究［J］. 工程力学，2004，21(1):56-60.

［9］Luongo A，Piccardo G. Non-linear galloping of sagged cables in 1:2 internal resonance ［J］. Journal of Sound and Vibration，1998，214(5):915-940.

［10］Liu Haiying，Zhang Qichang，Hao Shuying. A study on galloping for iced quad-bundled conductor ［J］. Journal of Vibration Engineering，2011，24(3):235-239.(in Chinese)刘海英，张琪昌，郝淑英. 覆冰四分裂导线舞动研究［J］. 振动工程学报，2011，24(3):235-239.

［11］Yan Z M，Yan Z T，Li Z，et al. Nonlinear galloping of internally resonant iced transmission lines considering eccentricity ［J］. Journal of Sound and Vibration，2012，331:3599-3616.

［12］Desai Y M，Yu P，Popplewell N，et al. Finite element modelling of transmission line galloping ［J］. Computers＆ Structures，1995，57(3):407-420.

［13］Li Li，Chen Yuankun，Xia Zhengchun，et al. Nonlinear numerical simulation study of iced conductor galloping［J］. Journal of Vibration and Shock，2011，30(8):107-111.(in Chinese)李 黎，陈元坤，夏正春，等. 覆冰导线舞动的非线性数值仿真研究［J］. 振动与冲击，2011，30(8):107-111.

［14］Yan Bo，Li Wenyun，Zhou Song，et al. Numerical simulation on galloping of quad-bundled conductor ［J］. Journal of Vibration and Shock，2010，29(9):102-107.(in Chinese)严 波，李文蕴，周 松，等. 覆冰四分裂导线舞动数值模拟研究［J］. 振动与冲击，2010，29(9):102-107.

［15］Liu Xiaohui，Yan Bo，Zhang Hongyan，et al. Nonlinear finite element analysis for galloping of iced bundled conductors［J］. Journal of Vibration and Shock，2010，29(6):129-133.(in Chinese)刘小会，严 波，张宏雁，等. 分裂导线舞动非线性有限元分析方法［J］. 振动与冲击，2010，29(6):129-133.

［16］Ma Yuquan. A new CR formulation and its application in geometrically nonlinear analysis ［J］. Science Technology and Engineering，2010，20(10):7476-7488. (in Chinese)马玉全. 改进CR 列式法及在几何非线性分析中的应用［J］. 科学技术与工程，2010，20(10):7476-7488.

［17］Yang Qi，Huang Jianyue. 3D geometric nonlinear simulation analysis of long span bridges ［J］. Central South Highway Engineering，2005，30(1):59-62. (in Chinese)杨 琪，黄建跃. 大跨度桥梁空间几何非线性仿真分析的研究［J］. 中南公路工程，2005，30(1):59-62.

［18］Wang Xucheng，Shao Min. Basic Principles and Numerical Simulation of Finite Element Method ［M］. Beijing:Tsinghua University Press，1995:549-550.(in Chinese)王勖成，邵 敏. 有限单元法基本原理和数值方法［M］. 北京:清华大学出版社，1995:549-550.