基于Danzig-Wolfe 算法的不正常航班旅客流恢复问题

王 莹，朱金福

(南京航空航天大学 民航学院，江苏 南京210016)

旅客流恢复是不正常航班恢复问题中必不可少的部分。如果在获取旅客订座信息、航班延误信息以及不正常航班恢复方案的基础上，站在全局的角度为行程受扰动的旅客重新安排航班，减少旅客退票和延误时间，就能实现航空收入和旅客满意度的大幅提高，实现航空公司和旅客的双赢。

JAFARI 和ZEGORDI 研究了不正常航班中飞机路线和旅客流同步恢复问题，采用Lingo 软件求解大规模线性规划问题［1］，其重新定义了恢复期的概念，并采用路线恢复而非航班恢复的概念，减小了问题的规模，但由于问题规模仍太大，求解效率不高。BISAILLON 等通过构建、修复、改进3个阶段解决飞机路线恢复、机型指派和旅客流恢复的问题［2］，其在构建完可行的飞机路线之后，采用最短路算法进行旅客路线的初始构建，为实现运送旅客人数的最大化，进行了放松延误时间的枚举尝试。其虽然考虑了旅客行程的衔接性，但枚举算法效率较低，且无法保证最优性。陆宏兰、高强、严俊等构建了延误成本最小的旅客流恢复模型，将问题转化为运输匹配问题，使用单纯形法进行了问题的精确求解［3-5］。他们虽然优化了存储方法和搜索策略，但由于要生成所有OD(origin-destination)对的可行路径，并要对所有OD 对进行路径重排，未能充分利用原方案，因此影响了求解效率。谢云双分析了航班延误补偿的经济效益问题，讨论了造成航班延误的原因以及影响赔偿金额的因素［6］。李雄等研究了航班延误引发的航空公司及旅客经济损失问题，详细分析了不正常航班成本构成、旅客赔偿和隐性损失［7］。文献［6］和文献［7］只进行了定性分析，未进行旅客流恢复的优化研究。

笔者在航班恢复方案的基础之上，根据航班订座信息，对行程受到扰动的旅客进行行程调整，将旅客流恢复问题处理成经典的多商品流模型，采用Danzig-Wolfe 算法进行求解，并通过一个实际规模的算例验证了该算法的可行性和效率。

1 旅客流恢复模型

1.1 模型假设

为简化模型和算法，对航空公司不正常航班恢复的实际操作规范和原则进行适当抽象，做以下假设:

(1)航班不正常发生后，已获得了航班恢复方案，调整旅客行程的过程中不对航班计划进行调整。

(2)只针对受扰动旅客进行行程调整。受扰动旅客通过签转方式获得新的行程;无法签转的旅客进行取消行程操作。

(3)航班容量限制为航班剩余座位数;OD 对的旅客需求已知，且不再变化。

1.2 构造时空网络

笔者采用时空网络建立旅客流恢复问题的多商品流模型。该多商品流模型中包含3 个主要信息，即商品、弧和成本，分别对应时空网络中的OD 对、航班和成本。

1.2.1 受扰动OD 对的构造

根据航班恢复方案和订座信息，采集衔接失败的旅客信息。由于航班信息以及旅客信息规模较大，如果根据旅客信息一一搜索对应的航班信息，效率将会降低。笔者首先根据航班恢复方案，采集受扰动的航班信息，结合航班订座情况，查看该航班上的旅客是否出现衔接失败情况，构造出受扰动的旅客信息，再将相同始发地和目的地以及相同计划离港时间的旅客分到一个OD 对中，对同一个OD 对进行订座旅客人数统计和预测，获得OD 对的旅客需求。

1.2.2 航班弧的存储

笔者根据航班恢复方案构造航班弧信息，建立航班弧的连接表，完成多商品流模型中弧的构建。航班弧的连接矩阵是一个大规模的稀疏矩阵，笔者采用十字链表存储航班弧连接，配合栈的使用，以便求解OD 对的可行路径。为了减小链表规模，十字链表中不包含取消航班弧。在初始化链表时，对航班恢复方案的航班出发时刻进行排序，以便对其子问题快速求解。

1.2.3 成本的表达

不正常航班旅客流恢复问题中的成本主要包括旅客行程取消成本、旅客延误成本，以及旅客中转成本。每一个OD 对选择一条航班路径(可能包括多个航班)均有对应的成本，而多商品流模型要求每一个OD 对选择每一条弧(即一个航班)均有相应的成本，这就需要对成本进行分解。

1.3 符号定义

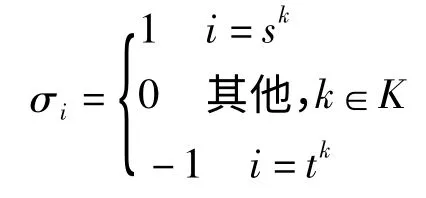
1.4 数学模型

1.4.1 多商品流模型

根据构造的时空网络和符号定义，可给出不正常航班旅客流恢复问题的多商品流模型如下:

式(1)为目标函数，要求总成本最小，包括运输成本和取消成本;式(2)～式(4)为约束条件，其中:式(2)为流平衡约束，要求每个时空节点满足旅客流量平衡，始发和目的节点保证实际运输的旅客流量与取消旅客流量之和等于OD 对旅客需求，由于实际运输的旅客流量大于等于零，必有yk≤dk;式(3)为航班弧的容量约束，要求改签到该航班的旅客总量不超过该航班的剩余座位数;式(4)为决策变量的非负约束，要求每个航班上乘坐的旅客人数和取消行程的旅客人数大于等于零且为整数。

1.4.2 成本的分解

如果首先计算整个路径对应OD 对的成本，再对各航段进行成本分摊，则需要生成各个OD对的所有可行路径，效率极低［8］。如图1 所示，笔者定义的航班弧有3 种，即取消弧、延误弧和中转弧，分别对应旅客流恢复问题中3 个主要成本。根据生成的OD 对信息，每一个OD 对均设有一条虚拟的取消弧，从始发地到目的地，取消弧的单位流成本为航班平均票价，假设取消一位旅客的订票不发生其他费用，只是减少了相应的机票收入。根据航班恢复方案，现行航班均为一条延误弧或中转弧，旅客行程最后一个航段决定旅客的总延误时间，属于延误弧，旅客延误成本与旅客总延误时间有关［9］，因此延误弧的成本为延误成本。其他始发和中转航段为中转弧，中转弧的成本为签转方案导致旅客出行不便的固定费用。为保证在成本相同的情况下，减少旅客签转，设定旅客原行程中的中转弧成本为零。

图1 成本分解示意图

2 Danzig－Wolfe 算法设计

笔者采用Danzig-Wolfe 分解算法求解多商品流问题，子问题是无容量约束的广义最短路问题。子问题的解构成主问题的一列。模型中式(3)为“难处理”约束条件，用来构造主问题，式(2)和式(4)为“易处理”约束，用来构造子问题。式(2)和式(4)构成的可行域X 是一个K 维空间封闭的凸多面体，其中任意一点可以表达成如下形式:

式中:L 为X 顶点指标集;xl为X 的一个顶点，是子问题的一个基本可行解，即k 个无容量约束最短路问题最优解的组合;λl为极点xl的凸组合系数且0 ≤λl≤1 。

2.1 主问题

根据模型的分解，笔者采用路径变量表示主问题:

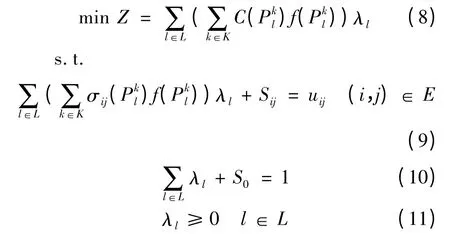
主问题是一个规模较小的线性规划问题，采用修正单纯形法配合热启动的方法进行求解。

2.2 子问题

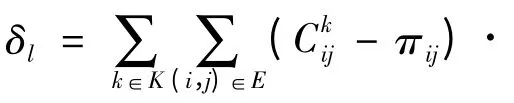
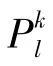
2.3 子问题搜索算法

子问题是k 个OD 对的广义最短路问题。笔者采用栈的存储结构和深度优先的搜索策略，配合十字链表的使用，用回溯的方法搜索OD 对的最短路。根据十字链表，可以快速地找到OD 对的延误弧，将该弧推入栈中，依次寻找前继中转弧入栈，直到找到可以作为该OD 对始发航班的弧。在栈的结构中设置一个存储单元，每一次入栈都进行一次标号，以记录当前累计成本，若弧A 出栈后，下一个引入的弧B 标号大于A，则舍弃，寻找同一级的下一个弧C。若无法找到可行路径或生成的路径成本大于取消弧成本，则将栈置空，取消弧入栈。同时，根据旅客最大可接受的中转次数(设为2 次)，可以设置栈的容量(设为3)，这样问题的规模就被大大缩小了。

2.4 Danzig－Wolfe 算法步骤

(1)解限制主问题，得到对偶变量π=(πij，π0);

(2)将对偶变量π 代入子问题，求解子问题，根据子问题的最优解得到第l 个极点xl;

(3)计算最小检验数δ = min w - π0。若δ ＜0，则将极点的组合系数λl作为入基变量，返回步骤(1);若δ ≥0 ，则停止迭代，求得主问题的最优解，即原问题的松弛解。

2.5 分枝定界算法求整数解

3 算例分析

笔者根据国内某航空公司一天的实际航班计划、订座情况、签转/赔偿方案设计出算例数据，如表1 所示。根据航空公司补偿标准，设定取消一名旅客行程的成本为航班平均票价，旅客延误每小时的成本为100 元，升舱无成本，降舱成本为舱位差价。

在硬件配置为Inter(R)Core(TM)2 Duo CPU，E7500 2.93 GHz，2 GB 内存的台式计算机上进行运算求解。共生成航班弧602 条，OD 对166 对，子问题迭代1 532 次得到最优解，耗时1分53 秒，减少航班取消旅客人数83.52%，挽回航空公司损失1 718 790 元，受扰旅客平均延误时间95 分钟，增加中转和延误成本561 537 元，运算结果如表2 所示。

表1 不正常航班实例数据

表2 旅客流恢复方案性能指标

4 结论

笔者建立了不正常航班旅客流恢复的多商品流模型，采用Danzig-Wolfe 分解算法对旅客流恢复问题进行了精确求解，该算法配合多种存储结构和搜索策略能够在符合实时决策要求的前提下，快速有效地提供受扰旅客的行程恢复方案。实例分析验证了模型的正确性和算法的有效性，表明采用笔者的方法不但可以减少旅客延误时间，还可以增加航空公司的收入，减少航空公司损失，解决航空公司不正常航班恢复问题。

［1］ JAFARI N，ZEGORDI S H.Simultaneous recovery model for aircraft and passengers［J］.Journal of the Franklin Institute，2011，48(7):1638 -1655.

［2］ BISAILLON S，CORDEAU J F，LAPORTE G，et al. A large neighborhood search heuristic for the aircraft and passenger recovery problem ［J］. A Quarterly Journal of Operations Research，2011，9(2):139 -157.

［3］ 陆宏兰.基于旅客行程的飞机航班一体化恢复研究［D］.南京:南京航空航天大学图书馆，2010.

［4］ 高强，严俊，陆宏兰. 不正常航班旅客流恢复方法［J］.科学技术与工程，2011，27(11):6670 -6673.

［5］ 严俊，高强，吴桐水.航班计划恢复中旅客流恢复问题的研究［J］.交通信息与安全，2012，30(1):20-23.

［6］ 谢云双.航班延误补偿的经济效益分析［J］.中国民用航空，2004，44(8):33 -34.

［7］ 李雄，刘光才，颜明池.航班延误引发的航空公司及旅客经济损失［J］.系统工程，2007，12(25):20-24.

［8］ BARNHART C，KNIKER T S，LOHATEPANONT M.Itinerary- based airline fleet assignment ［J］. Transportation Science，2002，36(2):199 -217.

［9］ BRATU S，BARNHART C.An analysis of passenger delays using flight operations and passenger booking data［J］.Air Traffic Control Quarterly，2005，13(1):1-28.