自由曲线轮廓数控刀具路径生成及加工

2013-12-23周永情李德明孙军伟

组合机床与自动化加工技术 2013年1期

周永情，李德明，孙军伟，王普

(1.河南质量工程职业学院机电系，河南平顶山 467000;2.河南平顶山姚孟电力工程有限责任公司，河南平顶山 467031;3.中电华元核电工程技术有限公司烟台分公司，山东烟台 265110)

0 引言

这里所指的自由曲线是指不能用数学公式表示，而是由一些型值点用平滑曲线连接而成的曲线。对于具有自由曲线截面轮廓的回转类零件，其加工相对困难，普通的车削划线困难，不能加工［1-5］。数控车削加工又具有以下两方面的困难:一方面如果采用手工编程，虽然知道型值点的坐标，但没有可用的插补方法，无法编制加工程序;另一方面采用自动编程，虽可以编制出加工程序，但编制的程序比较繁琐［6-10］。为了解决以上问题，本文对自由曲线进行分段，依据其曲率的具体情况，对不同的线段分别用圆弧和直线去拟合，获得圆弧和直线相关参数，然后用圆弧和直线插补生成加工刀具路径，实现了复杂曲线手工编程。

1 不规则曲线拟合的基本原理

1.1 直线拟合原理

当自由曲线曲率变化不大时时，可采用线形拟合法，即用最小二乘法求出拟合直线来代替，见图1。

图1 直线原理图

已知自由曲线某段曲线上一系列型值点的坐标i(XiYi)i = 1，2，…，n，要求拟和直线L(Y = Kx +b)，使其与理论自由曲线最逼近。

如果型值点i(XiYi)在直线L 上，则直线L 与自由曲线就没有误差;若点i 不在直线L 上，则存在误差:

为了消除误差正负号的影响，用误差的平方和Q来表示总体误差，总体误差公式为:

因此求拟合直线的问题就是根据(2)式求出能使Q(k，b)最小值的k 和b 的值，根据用求导的方法求极值的原理知，k 和b 的值可由下列方程组确定:

求出了拟合直线L 方程中的k 和b，即确定了拟合直线的空间位置，拟合直线与自由曲线的误差由(1)式计算。

1.2 圆弧拟合原理

设已知不规则曲线上一系列型值点的坐标为:I(yi1，yi2)，i = 1，2，3，…，n，如图2 所示。

图2 圆弧拟合原理图

要求用一个圆弧(y1－A)2+ (y2－B)2= R2来进行拟合，使复杂的曲线与圆弧最逼近;即使型值点到圆心的距离与半径的偏差最小，显然，如果I 点(yi1，yi2)在圆弧(y1－A)2+ (y2－B)2= R2上，则没有偏差，即(y'1－A)2+ (y'2－B)2= R2，如果型值点不在圆弧上则存在偏差，偏差为:

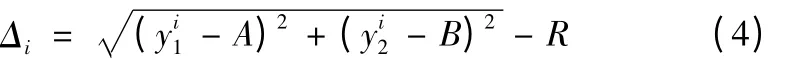
用误差的平方和Q 来表示总体误差，圆弧拟合总体误差公式:

因此求拟合圆弧的问题就是根据(6)式求出能使Q(A，B，R)最小值的A，B，R 的值，根据求导的方法求极值的原理知，A，B，R 的值可由下列方程组确定:

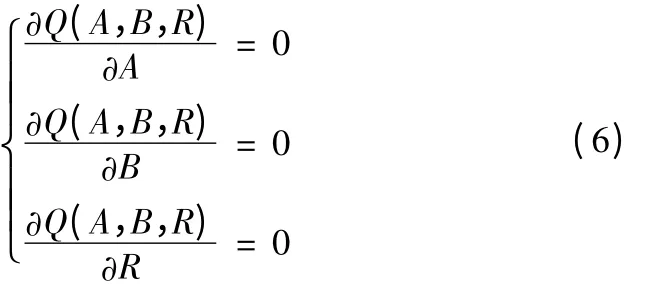
求出了拟合圆弧的方程中的A，B，R，即确定了拟合圆的空间位置，拟合圆弧与曲线的误差由(1)式计算，最大误差一般在两端点的型值点处，适当减少参与拟合计算的型值点个数，就可以使误差降低到允许的范围之内。

当曲线的曲率变化不大时，用几个圆弧就可以达到很好的拟合效果。当曲线的曲率变化太大时，把曲线分成多段，增加拟合数量，也能达到最逼近曲线的效果。

当自由曲线曲率较大时，特别是两个型值点之间曲率变化不大而曲率较大时，可采用线形拟合法，即用求出拟合直线来代替自由曲线，能达到更好的拟合效果

2 刀具路径生成实例与加工

本文以某成型刀具刀盘的车削加工为例，介绍其刀具路径生成的全过程。某成型刀具刀盘的轴截面轮廓为22 个型值点组成的自由曲线(如图1 所示)，为了编制数控加工程序方便，对各个型值点坐标进行平移，建立加工坐标系如图3 所示。

图3 刀盘加工坐标系

2.1 拟合计算

对曲线进行分段，依据刀盘轮廓曲线的曲率变化情况(如图1 所示)，按顺时针方向，1－5 点、5－9点、9－11 点、11－13 点、13－15 点、15－17 点、17－19 点对应曲线曲率相对较大且变化不大，分为7 段，用圆弧拟合;19－21 点、21－22 点对应曲线曲率相对较小且变化不明显，分为两段，用直线拟合。

第一段拟合计算:这一段共5 个型值点，代入(5)式，依据(6)式列方程组，求解得到拟合圆弧半径R1 = 357.096，圆心坐标(－136.371，360.925)。

第二段拟合计算:这一段共4 个型值点，代入(5)式，依据(6)式列方程组，求解得到拟合圆弧半径R1 = 133.185，圆心坐标(－188.055，421.150)。

第三段拟合计算:这一段共3 个型值点，代入(5)式，依据(6)式列方程组，求解得到拟合圆弧半径R1 = 82.455，圆心坐标(－255.177，465.945)。

第四段拟合计算:这一段共3 个型值点，代入(5)式，依据(6)式列方程组，求解得到拟合圆弧半径R1 = 44.217，圆心坐标(－163.810，433.684)。

第五段拟合计算:这一段共3 个型值点，代入(5)式，依据(6)式列方程组，求解得到拟合圆弧半径R1 = 52.891，圆心坐标(417.807，534.885)。

第六段拟合计算:这一段共3 个型值点，代入(5)式，依据(6)式列方程组，求解得到拟合圆弧半径R1 = 96.290，圆心坐标(236.837，449.848)。

第七段拟合计算:这一段共3 个型值点，代入(5)式，依据(6)式列方程组，求解得到拟合圆弧半径R1 = 157.788，圆心坐标(236.837，449.848)。

第八、九段依据曲率情况用直线拟合。

第八段拟合计算:这一段共3 个型值点，代入(2)式，依据(3)式列方程组，求解得到斜率K =－15.3，b = 225.675。

第九段拟合计算:这一段共3 个型值点，代入(2)式，依据(3)式列方程组，求解得到斜率K =－27.32，b = 372.21。

确定了圆弧半径、圆心坐标和直线的斜率、截距，就确定了圆弧和直线的坐标位置，为了检验分段的合理性和拟合的精度，把经过坐标平移的型值点坐标导入AUTCAD 软件，生成标准的刀盘轮廓曲线，然后绘制拟合的圆弧和直线，拟合前后曲线如图4、5所示。通过测量，拟合偏差很小，对于刀盘的加工，这些偏差在可允许的范围之内，可见本文的分段是基本合理的。要想进一步提高拟合的精度，只需增加分段数量就可以，只不过相应的拟合计算量也增加。在满足要求的前提下，尽可能用较少的线段拟合，这样可以减少计算，简化程序的编制。

图4 刀盘截面曲线

图5 拟合后的曲线

知道了圆弧半径、圆心坐标和直线的斜率、截距，还不能满足数控加工程序编制需要，还要知道圆弧和直线两端点的坐标，两端点坐标的确定可以通过两种途径，一是列方程组，计算依次求出相邻圆弧和直线的交点即为端点坐标，只是计算量比较大。二是绘图法，利用CAD 软件绘出各个圆弧和直线，通过标注测量求出端点坐标，这种方法比较简便，本文就采用这种方法。依次求得7 个圆弧和2 条直线端点坐标如下:

(－21.69，32.44)(－18.84，46.63)(－ 9.51，59.84)(－2.41，62.73)(2.35，62.37)(6.25，59.58)(9.62，54.12)(11.72，46.36)(12.35，36.72)(12.57，30.71)。

采用直线插补和圆弧插补，手工就可以编制刀具加工路径，完成零件加工。

2.2 数控程序编制

首先进行加工工艺分析，此为典型的盘类零件，在普通数控机床上就可以加工，夹具选用三抓卡盘，刀具选用普通外圆车刀，分为两头加工，一端加工完成后留一定长度的定位外伸，通过以上计算，加工相关参数已经完备，采用G71 复合循环指令进行编程，然后选择刀具及装夹方式，刀具:1 号刀为90°外圆刀，刀尖角为55°;2 号刀为切断刀，刀位点在左刀尖，刀宽为3mm;装夹:采用三爪卡盘。最后确定加工路线。

编制程序如下: