高性能交流伺服系统中的控制方法*

呼文豹，郭锐锋，王志成，李 杰

(1.中国科学院 研究生院，北京 100049;2.中国科学院 沈阳计算技术研究所，沈阳 110168)

0 引言

交流伺服电动机模型是一种强耦合、时变的非线性系统，并且运行时会受到不同程度的外界干扰，其控制技术十分复杂，所以交流伺服系统性能的好坏直接受所采用控制技术的影响，高质量的控制技术可以弥补硬件设计的不足，同时还能改善伺服系统的控制性能。高性能交流伺服系统对控制技术的要求主要表现在:如何使系统具有较高的动静态精度和较快的响应速度，并且如何使系统对参数变化以及外界扰动具有不敏感性。因此，交流伺服系统控制技术的研究具有十分重要的意义。

控制方法是高性能伺服控制系统控制的核心，有必要对交流伺服系统及其先进的控制方法的发展有一个全面的了解，本文正是基于这一目的，对高性能交流伺服系统的控制方法做了较为全面的综述，分析了经典控制方法、现代控制方法、智能控制方法以及复合控制方法，尽可能反应近几年来的最新研究，了解各种控制方法的优劣性，并对高性能伺服系统控制技术的发展进行了展望。

1 经典控制方法

经典控制方法以单输入－单输出的线性定常系统为基础，描述系统时采用传递函数法，利用拉普拉斯变换作为数学工具，以控制系统的时间响应和频率特性为着眼点来进行系统分析和设计［1］。它主要包括PID 控制、矢量控制和恒压频比控制等，下面以前两种为例介绍在实际中的应用。

1.1 PID 控制

工业控制中常用的方法是PID 调节器，尽管随着现代交流调速技术的发展，出现了一些新型的控制算法，从理论上分析，许多控制方法都能实现良好的电机动静态特性，但是算法本身的复杂性，并且对系统进行模型辨识比较繁琐，然而传统的PID 控制器具有稳定性好、工作可靠和调节方便的优点，使用中不需精确的系统模型等先决条件，使得在数控系统控制中，PID 调节器更容易实现预期的效果。PID的控制原理框图如图1 所示。

图1 PID 控制原理框图

PID 控制的控制规律:

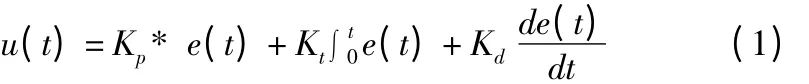
Karam 等［2］，提出了一种PID 控制器，是电动液压伺服驱动系统(EHSAS)用来控制摇动液压缸的角位置的，PID 增益参数利用遗传算法(GA)进行优化，相对于常规PID 控制器和补偿控制器，基于遗传算法的PID 控制器在控制摇动液压缸的角位置上的具有良好性能。

但是PID 控制的问题在于参数整定，一旦整定计算好后，在整个控制过程中都是固定不变的，而实际系统的状态和参数会发生变化，过程中会出现状态和参数的改变，而且常规PID 控制参数仅凭借技术人员的经验进行调节的，具有一定的局限性。李等［3］，在EtherCAT 网络伺服运动控制系统平台下，研究了基于DSP 的电机伺服控制，并采用模糊PID控制方法，实时自动调整PID 控制参数以修正电机的运行误差，保证系统的输出在一定精度内跟随指令变化，提高了伺服的跟踪精度以使控制达到较好的效果。

1.2 矢量控制

矢量控制，也称为磁场定向控制。上世纪70 年代西门子工程师F.Blaschke 首先提出异步电机矢量控制理论来解决交流电机转矩控制问题。

矢量控制具体是将异步电动机的定子电流矢量分解为产生磁场的电流分量(励磁电流)和产生转矩的电流分量(转矩电流)分别加以控制，并同时控制两分量间的幅值和相位，即控制定子电流矢量，所以称这种控制方式称为矢量控制方式。它是基于电动机的动态数学模型，具有与直流电动机调速类似或者更优越的控制性能，图2 是矢量控制系统原理结构图。

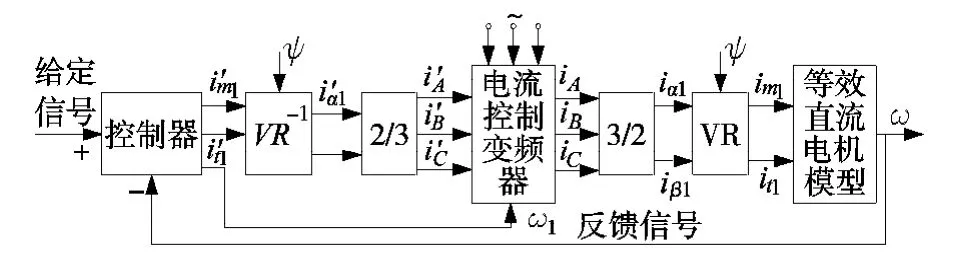
图2 矢量控制系统原理结构图

薛等［4-5］，提出的控制系统中的电流环采用的是Id=0 的矢量控制策略，这样，可实现最大转矩电流比。依据的原理是:PMSM 的电枢反应主要是由定子电流的q 轴分量Iq引起的，在实际应用中，对永磁同步伺服电动机的电枢反应一般忽略不计。定子电流的d 轴分量Id相当于激励电流。在额定转速下，采用恒定转矩调速方式，在一定的定子电流幅值下能够输出最大的转矩，因此最佳的控制方式是使定子电流与d 轴正交，也就是保持Id=0。

此外，矢量控制可以使得变频器根据频率和负载情况实时的改变输出频率和电压，因此其动态性能相对完善，矢量控制具有能对转矩进行精确控制、系统响应快、调速范围广、加减速性能好等特点。在现代电机驱动器中广泛应用矢量控制，目的就是得到快速动态响应和更有效的操作［6］。矢量控制方法的提出具有划时代的意义，然而在实际应用中，由于转子磁链难以准确观测，系统特性受电机参数的影响较大，且在等效直流电动机控制过程中所用转换较为复杂，使得实际的控制效果难以达到理想的分析效果。

随着生产过程自动化水平的提高，控制系统的任务越来越复杂，控制精度要求也越来越高，因此，建立在状态空间分析方法基础上的现代控制理论便迅速地发展起来。

2 现代控制方法

经典控制方法隐含着两个前提，一是要求对象的模型是精确的、不变化的、线性的;二是操作条件和运行环境是确定不变的。随着应用对控制精度和性能要求的提高，考虑控制对象变化和非线性的影响等，才能达到预期效果。在这种需求的推动下，一些新的控制方法得以产生，并在工业控制中得到应用和发展。下面以滑模控制和自适应控制为例，介绍它们在工业控制中的应用。

2.1 滑模控制

滑模控制(sliding mode control，SMC)也称作滑模变结构控制，本质上是一类特殊的非线性控制，且非线性表现为控制的不连续性。这种控制策略与其它控制的不同之处在于:系统的结构并不固定，而是可以在动态过程中，根据系统当前的状态有目的地不断变化，迫使系统按照预定滑动模态的状态轨迹运动。由于系统的特性和参数只取决于设计的切换超平面而与外界干扰没有关系，所以滑模变结构控制具有很强的鲁棒性。

尽管滑动模态对加在系统上的干扰和系统的摄动具有完全的自适应性，但是基于该方法的控制器也存在一定的劣势，即系统控制器的输出会有抖动现象，例如，交流伺服系统的高频率振动，会降低系统性能，导致系统的不稳定［7］。

谢等［8］，提出一种针对永磁同步电机交流伺服系统的串级滑模变结构控制方案，其在速度环滑模控制器中引入积分环节，减小了转矩的脉动，位置环采用准滑模变结构控制策略，极大地抑制了位置输出的抖动。朱等［9］，针对永磁同步电动机位置伺服系统负载例句和转动惯量变化大、干扰力矩强的特点，提出了一种串级复合滑模变结构控制方法，其中速度环采用带有积分补偿的滑模控制器以消除力矩的抖动，而位置环引入复合滑模变结构控制策略，在位置误差较大时采用滑模控制，在小位置误差时采用复合前馈控制，从而达到消除滑模抖振的目的。

Liu 等［10］也提到相似的结论，在高精度低速伺服系统中，滑模变结构控制能达到传动系统的性能要求，在低速跟踪性能上能得到较好的效果，但是存在抖振。提出的模糊滑模控制，引入了降低抖振的模糊规则，能够有效地降低滑动模块控制的震荡，提高了低速跟踪性能。

将滑模变结构控制应用于交流伺服系统，必须解决传统开关控制带来的抖动问题。常用的方法是，在开关点附近将控制量连续化。滑模控制器的动态设计就是利用线性系统的动态滤波器理论进行滑模控制器设计的方法。

2.2 自适应控制

自适应控制的研究对象是具有一定程度不确定性的系统，即描述被控对象及相应的数学模型不是完全确定的。任何一个实际系统都具有不同程度的不确定性，从系统内部来讲，描述被控对象的数学模型的结构和参数在运行期间有变化，作为外部环境对系统的影响，可以等效地用一些不可预测的扰动来表示，此外，还有一些测量时产生的不确定因素，面对这些客观存在的不确定性，如何设计适当的控制方法，这就是自适应控制所要解决的问题。

Zhou 等［11］，提出来一种基于反推控制技术的实时非线性自适应速度控制体制，应用于永磁同步伺服电动机。在控制器的设计中，利用输入输出反馈的线性化补偿系统的非线性化，自适应反推控制方法的应用是源于一种控制体制，该体制对参数的不确定性和负载转矩干扰具有鲁棒性。所提的控制体制能够跟踪速度参照信号，该信号是一个参照模型在不确定参数和负载转矩干扰的情况下产生的。

Qu 等［12］，提出了自适应逆控制交流永磁同步电动机伺服系统，采用位置、速度、电流三环控制结构，其中位置环采用自适应逆控制策略，其基于对给定信号 采用逆控制与自适应控制相结合的思想，对给定信号和扰动信号进行控制，从根本上消除了噪声对位置输出的影响，较好地解决了交流伺服系统高性能控制的问题。

现代控制方法以状态空间描述作为数学模型，实质上是一阶微分或差分方程组，适应于多变量、非线性、时变系统，可以处理多输入－多输出系统，能获得某种最优解，但是不能处理频率特性。经典的或现代的控制方法都依赖于具体的数学模型，不能从根本上解决复杂和不确定系统的控制问题，为此，人们必须建立新的方法用于复杂的系统控制。

3 智能控制方法

智能控制是一个完全独立的思想，它的控制模型是基于语言模型，能够解决控制对象、环境和任务比较复杂的系统。智能控制按实际效果进行控制，并不依赖被控对象的模型，在控制中可以解决系统的不确定性和不精确性问题。其控制理论体系日趋庞大，其中三种比较经典的控制是模糊控制、神经网络控制和鲁棒控制，下面以前两种为例，介绍它们的应用情况。

3.1 模糊控制

模糊控制是一种利用模糊数学的基本思想和理论的控制方法。传统的控制理论对于明确系统有较强的控制能力，但对于复杂或难以精确描述的系统，很难达到理想的控制效果，因此，尝试用模糊数学的方式处理这方面的控制问题。

模糊控制不依赖于被控对象的精确数学模型，具有较强的鲁棒性，对被控对象的参数变化不敏感，可以有效地克服交流伺服电机中的非线性、时变、耦合等因素的影响。但是，单纯地使用模糊控制，要求工作人员有丰富的经验，控制精度相对较低。

Wang 等［13］，通过将模糊逻辑和自适应算法相结合，提出了一种新的交流伺服系统的位置控制方法。该方法通过自适应算法在线学习，可以自动调整控制器参数以获得最优的控制输出，而不需要被控对象的精确数学模型，该算法具有良好的自动调节和位置跟踪性能，具有较高的鲁棒性和跟踪精度，能很好地解决模型不确定系统的位置伺服控制问题。

由于交流伺服系统存在参数时变、负载扰动以及交流电动机自身和被控制对象的严重非线性特性、强耦合等不确定性因素，用常规的PID 控制不能满足要求，因此，Zhang 等［14］，提出了一种具有调整因子规则的自校正模糊控制交流伺服系统，可以满足不同时域的控制要求，按不同的规则生成模糊控制查询表，使得模糊控制规则可以在线调整，极大的提高了交流伺服系统的控制性能。

3.2 神经网络控制

神经网络控制是20 世纪80 年代末期发展起来的自动控制领域的前沿学科之一。它是智能控制的一个新的分支，为解决复杂的非线性、不确定系统的控制问题找到了新的途径。神经网络是从微观结构与功能上对人脑神经系统的模拟建立起来的模型，具有模拟人的部分智能的特性，具有非线性特性、学习能力和自适应性，适合于处理难于用模型或规则描述的。

神经网络与其它传统方法相结合，如神经自校正控制、神经PID 控制以及神经模型参考自适应控制等，这将推动人工智能和信息处理技术不断发展。近年来，人们尝试用神经网络控制技术应用于交流电机驱动控制系统中，使用它调节系统具有很好的噪音抑制特性、容错性和扩展性，是未来电机控制技术的一个重要的发展方向。

王等［15］，设计出了一种闭环前馈控制交流伺服系统，利用了神经网络和前馈控制的优良特性，将逆控制方法引入了高精度交流伺服系统，在不改变系统闭环稳定和不需要知道对象精确模型的基础上建立起具有较高鲁棒性和自适应性的控制系统，应用神经网络的自适应能力和逼近能力求得交流伺服系统的逆模型，闭环与神经网络技术的结合，保证了系统的稳定性。

Lin 等［16］，提出了一种用于永磁同步电动机伺服系统的PID 神经网络控制。调查了PIDNN 在PMSM伺服系统中的控制规则，首先引入了PMSM 的数学模型，应用PIDNN 的在线学习、跟踪和校正能力，并将提出的PIDNN 控制器与传统的PID 控制器进行了比较，PIDNN 控制规则在PMSM 伺服系统中具有良好的跟踪和实时控制性能。

4 复合控制方法

无论是经典控制方法、现代控制方法，还是智能控制方法，每种控制方法都有它们各自的优点，但不可避免地存在着一定的缺陷。在控制行业中，单纯地靠一种控制方法很难达到理想的效果，因此，将不同的控制方法相互渗透，互济优势，结合成复合的方法，成为获得更优越的控制方法的一种必然趋势。目前复合控制方法主要有两种形式:一是在PID 控制方法的基础上添加新型控制方法;二是采用多种新型控制方法。复合控制方法的类型很多，随着研究的进行还在不断地增加，下面介绍几种典型的复合控制方法的应用。

Muhammad 等［17］，提出了一种优化的混合模糊比例微积分控制器(HFPID)，此控制器是基于PID和模糊算法的组合控制器，用于具有非线性因素的交流伺服系统，本文结合PID 和模糊逻辑控制器的优点获取精确的跟踪性能。提出的优化的HFPID，具有一些适应异常进化算法的比例因子，得到了良好的收敛可靠性和抑制非线性影响的鲁棒性能。

徐等［18］提出了一种基于PMSM 的智能型位置伺服控制系统方案，系统的位置环采用模糊滑模控制，并由主、从两个模糊控制器组成，主控制器用于产生输出控制量，从控制器在线调节主控制器的输出比例因子，以抑制滑动模态的抖振，该智能型位置伺服控制系统在大、小位置给定下均能够同时获得定位无超调和定位时间的准确优化控制，具有良好的动静态性能。复合控制方法除了以上提及的几种，还有自适应模糊滑模控制方法［19］，模糊神经网络控制方法［20］，模糊自适应控制方法［21］等。

5 总结与展望

在现代工业日趋综合化的形势下，高性能伺服控制方法从经典的向现代和智能控制方法的发展，产生了一系列的新型控制方法。控制方法的广泛使用为工业控制的发展提供了良好的技术支撑，但如何保证伺服系统的高效性是研究的关键。本文总结了近几年有关高性能伺服系统控制方法的文献，并对控制方法进行了分类，介绍了控制方法在实际中的应用。

随着交流伺服系统应用领域的不断扩大，用户对伺服系统技术的要求也越来越高，因此，未来伺服系统的性能必将会进一步的完善。笔者认为，如若提高伺服系统的性能，可以在软件上采用新的控制理论，提高运算的速度和电流控制的精度;也可以从伺服电机的本身出发，采用新的结构，进一步加大输出转矩，优化输出效率;另外，从神经网络控制具有噪音抑制特性出发，伺服系统可以在低噪音方面进行改进，弱化对环境的要求以及减少外界的干扰，依此来增强系统对环境的适应性。

［1］海老原大树，编，王益全，刘军，等.译. 电动机技术实用手册［M］. 北京:科学出版社，2006.

［2］Karam M. Elbayomy，Jiao Zong-xia，Zhang Hua-qing. PID Controller Optimization by GA and Its Performances on the Electro-hydraulic Servo Control System［J］. Chinese Journal of Aeronautics，2008(21):378－384.

［3］李木国，李响，刘达. 基于DSP 的电机伺服系统中的模糊PID 控制［J］. 测控技术，2011，30(6):64－67.

［4］薛青，花银群，程广贵，等. 基于永磁同步电机的高性能交流伺服控制系统研究［J］. 科学技术与工程，2009，9(1):29－33.

［5］王翔，马瑞卿，吉攀攀. 基于模糊PI 控制的PMSM 位置伺服系统仿真［J］. 微电机，2010，43(3):52－55.

［6］ZHANG Ying-chao，ZHAO Zheng-ming，GUO Wei，et al.High Performance Position Control System Based on SR-PM Motor［J］. Tsing Hua Science and Technology. ISSN.1007-0214. 17/19. 2007，12(5):614－619.

［7］Micheal Defoort，Thierry Floquet，Annemarie Kokosy，et al.A novel higher order sliding mode control scheme［J］. Systems ＆ control Letters，2009(58):102－108.

［8］谢成祥，曾庆军，许德. 交流伺服系统的串级滑模变结构控制仿真研究［J］. 华东船舶工业学院学报(自然科学版)，2001，15(1):43－47.

［9］朱玉川，李志刚，马大为，等. 永磁交流位置伺服系统串级复合滑模控制［J］. 系统仿真学报，2007，19(12):2779－2882.

［10］LIU Hui-bo，Zhou Hai-jing，Feng Zheng. The Application of Sliding Mode Control in High Precision Low Speed Servo System［J］. Advanced Electrical and Electronics Engineering，LNEE，2011，87:495－502.

［11］ZHOU Jian-guo，WANG You-yi. Real-time nonlinear adaptive backstepping speed control for a PM synchronous motor［J］.Control Engineering Practice，2005(13):1259－1269.

［12］QU Yong-yin，ZHOU Zhen-xiong. The Adaptive Inverse Control Strategy Research of Servo System for Permanent-Magnet Synchronous AC motor［J］. 2008 Chinese Control and Decision Conference (CCDC 2008):3152－3155.

［13］WANG Bao-ren，ZHANG Cheng-rui，JIA Lei. Study of Fuzzy Logic Based Adaptive Position Control used for AC Servo System［J］. Proceedings of the 6th World Congress on Intelligent Control and Automation，Dalian，China，2006(6):21－23.

［14］ZHANG Chun-yan，YU Shu-fang，ZHANG Liang. The Application of Fuzzy Control in AC Servo System［J］. Journal of Xinjiang University(Natural Science Edition)，2004(1):426－429.

［15］王永林，王杰. 神经网络前馈逆控制在交流伺服系统中的应用［J］. 郑州大学学报(自然科学版)，2000，32(3):51－56.

［16］LIN Li-xiong. A PID Neural Network Control For Permanent Magnet Synchronous Motor Servo System［J］. The 5th International Conference on Computer Science ＆ Education Hefei，China. 2010，24－27(8):1174－1178.

［17］Muhammad Babar Nazir，WANG Shao-ping. Optimization Based on Convergence Velocity and Reliability for Hydraulic Servo System［J］. Chinese Journal of Aeronautics，2009(22):407－412.

［18］徐宏培，吴新开，彭双光，等. 基于PMSM 的智能型位置伺服控制系统研究［J］. 电气传动自动化，2011，33(1):6－10.

［19］Rong-Jong Wai，Chih-Min Lin，Chun-Fei Hsu. Adaptive fuzzy sliding-mode control for electrical servo drive［J］.Fuzzy Sets and Systems，2004(143):295－310.

［20］Erdal Kayacan，Yesim Oniz，Ayse Cisel Aras，et al. A servo system control with time-varying and nonlinear load conditions using type-2 TSK fuzzy neural system［J］. Applied Soft Computing，2011(11):5735－5744.

［21］JING Na，REN Xue-mei，Guido Herrmann，et al. Adaptive neural dynamic surface control for servo systems with unknown dead-zone［J］. Control Engineering Practice，2011(19):1328－1343.