激光操控双射频Paul囚禁离子的局域运动

郝红军，贾拴稳

(安阳师范学院物理与电气工程学院，中国安阳 455000)

由于离子阱技术［1］的成熟，以及离子阱技术在量子计算［2-3］等方面的重要应用，研究囚禁单粒子运动的控制问题是很有意义的.容易实现操控条件的离子阱系统中，为研究粒子的经典或量子力学动力学特征，开辟了一个实验和理论研究的重要领域.

囚禁粒子在含时驱动场中，常常会表现出丰富的动力学特性［4-5］.对于单频Paul 阱系统，我们不能求出运动方程的精确解［6］，但是在双射频Paul 阱系统中［7-8］，在一定条件下，系统存在精确解.本文研究当双射频Paul 阱系统加上一个激光线性控制时囚禁离子的运动性质.通过精确求解受控双射频Paul 阱系统Schrodinger 方程发现，当外加控制的频率和Paul 阱的频率比值取某些特定值时，双射频Paul 阱内粒子运动出现局域化状态，这一现象与1986年Dunlap 和Kenkre［9］发现的动力学局域现象相似.他们理论计算发现，在无穷晶格链系统中，当驱动场强与频率的比值取零阶Bessel 方程的根时，体系出现局域态.操控频率与Paul 阱频率的比值相比较驱动场强与频率的比值，存在很大的不同.在通常共振现象中，操控频率与体系固有频率是强烈相关的，这里局域化现象的出现与共振现象有着某种相反的特征，因此这里发现的是一种新的动力学局域化现象.

1 理论模型与计算

考虑囚禁在双射频Paul 阱内单个离子受到激光场控制时的一维运动，体系的Hamilton 量为

式中，m 是离子质量;p 是离子x 方向的动量算符;Paul 阱含时弹性系数

操控激光场近似为频率为Ω 的控制电场

式(2)中αx和q1，2是与Paul 阱有关的无量纲参数［1］;ω 为Paul 阱2 个射频驱动中的低射频;式(3)中ε0为外加控制激光场的强度.下面求解体系的量子态.

体系的量子态ψ(x，t)满足Schrodinger 方程

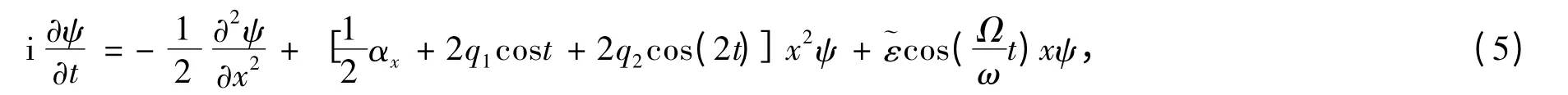
设量子态ψ(x，t)的函数形式为

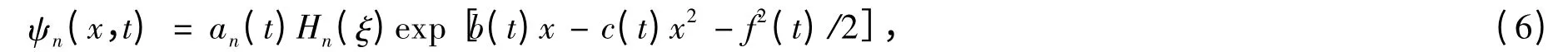
其中a(t)，b(t)和c(t)是时间的复函数，Hermite 多项式Hn的宗量

ξ=e(t)x－f(t)，

e(t)和f(t)是实函数.把(6)式代入(5)式，并利用Hermite 多项式性质

得到

式中变量上的“·”表示对时间求导.(7)是复Riccati 方程，通过变换

得到

(13)式是双射频形式的Mathieu 方程，如果q2=0，(13)式就变为通常单频Paul 阱的Mathieu 方程，它没有精确解，只能通过各种近似方法求解.双射频形式的Mathieu 方程，在某些参数条件下有精确解［7，12］，如参数满足条件

则(13)式有2 个线性无关的精确解

φ2的一阶导数分段连续.φ1和φ2的任意复系数叠加得到(13)式的通解

由(8)得

复积分常数b0由体系的初始条件决定.把b 和b0均写为实部与虚部分离的形式b(b0)=b1(b01)+ib2(b02)，则

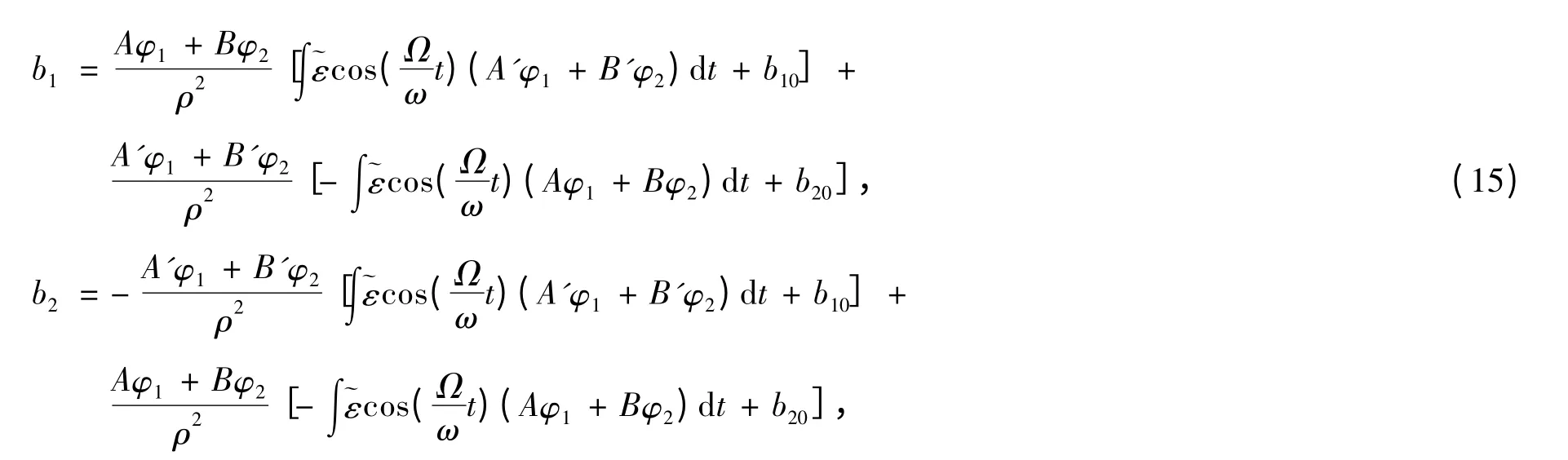
式中An是归一化常数.

到此，(6)式中各个未知的时间函数都已求出，我们得到Schrodinger 方程(4)的一个精确解

2 结果分析和讨论

从(16)式波函数ψn(x，t)的形式可以看出，只有实指数函数中C0≠0 时，ψn(x，t)才有解，所以在(14)式构造φ 时，要求满足条件AB'－A'B ≠0，本文将令A=B'=1，A'=B=0，即φ=φ1+iφ2，C0=1.容易看出态ψn(x，t)的位置几率分布是一个波包列［11，13］，ρ 反映波包列的宽度和高度，b 的实部b1决定波包列中心的位置，也就是外加驱动决定波包列中心的运动，让(17)式ξ=0 可以计算得到波包列的中心位置在xc=ρ2b1.如果取初始时刻波函数的波包列中心在原点，则(15)式中与初始条件有关的积分常数b10=b20=0，这时波包列中心位置

通过计算可以知道态ψn(x，t)的位置平均值等于波包列中心位置坐标

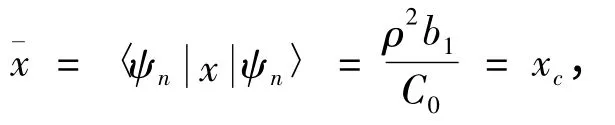
态ψn(x，t)的动量平均值

式(18)实际上也是把体系作为经典系统处理时，初时刻静止在原点粒子的运动轨迹方程.由于φ2的时间一阶导数在点2nπ 处不连续，依据Ehrenfest 定理［14］，要求在(19)式中，，这个方程可以用作图法求解.当Paul 阱参数q1取典型值0.4，=1 时，通过数值计算，得到的关系如图1.

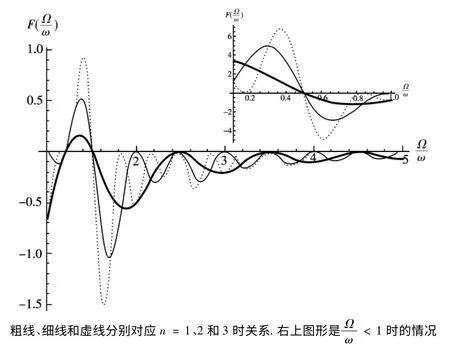
图1 与的关系Fig.1 The integraldt as a function of.The thick，thin and dash curves correspond to n=1，2 and 3，respectively.The inset displays the corresponding results for.

下面依据(18)式数值计算波包列中心的运动情况.Paul 阱参数q1取典型值0.4，.图2 给出初时刻波包列中心在原点的量子态当Ω/ω 取不同值时，波包中心xc2 个周期内的运动轨迹(时间和长度单位分别取ω－1和，图中坐标t 和xc无量纲)，图(a)、(b)和(c)分别对应Ω/ω=1.5，2.5，9.5.从图中看出，粒子从初始位置0 处开始向正方向运动，做基频振动周期为4π 的周期运动(Paul 阱的宏运动周期)，随Ω/ω增加(控制频率增加)，粒子振动加快，当Ω/ω=9.5 时，振幅明显出现“拍”的现象;还可以发现，在t 等于2π和6π 处，离子受到向x 正方向的反冲.

图2 q1=0.4，，初时刻波包中心在原点的量子态，在Ω/ω 取不同值时，波包中心xc 运动轨迹(时间和长度分别取单位ω－1 和，t 和xc 无量纲).(a)Ω/ω=1.5 时，在2π 和6π 处有向x 正方向反冲;(b)Ω/ω=2.5 时，振动频率增加;(c)Ω/ω=9.5 时，出现“拍”现象Fig.2 The motion of the wave-packet centre with q1=0.4，and xc(t=0)=0.The time t and distance xc are normalized in the units of ω－1 and，respectively.(a)For Ω/ω=1.5，there are recoils in the xc-direction at t=2π and 6π，(b)For Ω/ω=2.5，the vibration frequency increases，(c)For Ω/ω=9.5，the phenomenon of beats appears

为了便于比较，图3 给出Ω/ω 不满足局域运动态条件时的数值计算图像，图3(a)和(b)分别对应Ω/ω=1.48 和2(坐标等条件与图2 相同)，这时由于动量平均值在2nπ 处不连续，所以这时的运动是不稳定态，不会在Paul 阱内长时存在.我们看到，图3(a)与图2(a)的区别是，前者在t=2π 和6π 处粒子受到的反冲不能与运动相“平衡”，这与经典物理中振动态稳定要求策动与运动平衡相一致.但图3(b)中粒子受到的反冲与运动“平衡”，为什么它也是不稳定的态呢?

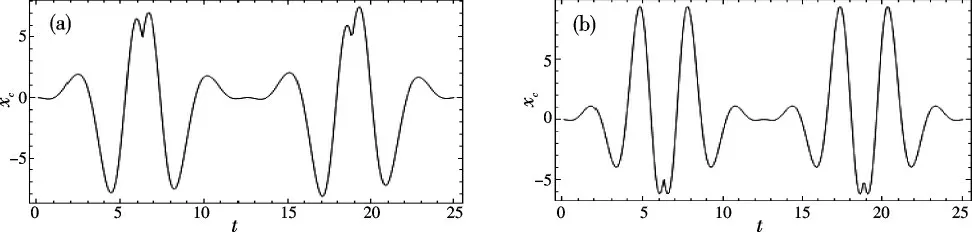
图3 Ω/ω 取值不满足稳定态要求时xc 的轨迹，条件与图2 相同.(a)Ω/ω=1.48 时，在t=2π，6π 处，反冲与运动不平衡;(b)Ω/ω=2 时，在2π 和6π 处反冲向负方向Fig.3 The motion of the wave-packet centre with Ω/ω values that do not satisfy the stable state condition.The same units as those in Fig.2 are used.(a)For Ω/ω=1.48，the recoil motion is imbalance at t=2π，6π，(b)For Ω/ω=2.5，there are recoils in the negative xc-direction at t=2π and 6π

我们看初始条件一样但没有控制电场时，Paul 阱内经典稳定运动解xc=eq1costsin(t/2)的图像［7］(图4)，它就是φ1=eq1costsin(t/2)的图像，它也可以由(18)式加齐次相，再令=0 数值计算得到.图4 中，在t=2π和6π 处，粒子向负方向运动的速率最大，因此我们可以理解图3(b)不稳定态是由于反冲向负方向与系统本征运动同相;而图2中运动的反冲向正方向，与系统本征运动反相，因此是稳定的.

3 结论

本文发现在激光操控的双射频Paul 势阱系统中，控制频率与双射频Paul 阱的一个射频比为某些离散值时，受控离子会出现动力学局域化现象，它与Dunlap 和Kenkre 发现的无穷晶格系统中，驱动场强ε 与驱动频率ω 比值为某些值时发生的动力学局域化现象虽然类似但不一样.由于离子阱系统相比晶格系统人为控制难度较小，这里的现象应该更容易在实验中发现，有望能借助相关实验验证其存在性.需要指出的是，这里的动力学局域化条件Ω/ω=n+1/2(ω 是Paul 阱射频，Ω是驱动频率)，与近年发现的微波诱导零电阻状态现象［15－16］的条件很相似.零电阻现象是当微波频率ω 与电子回旋频率ωc满足关系ω/ωc=n+1/2 时，二维电子气电阻存在最小值，本研究对该现象的机理探讨有一定的参考价值.

图4 没有驱动时(=0)，Paul 阱的一个本征运动，即(13a)式，其他条件与图2 相同，在t=2π 和6π 处，粒子向负方向运动Fig.4 The motion of an eigenstate with manipulation not existing in the Paul trap.The particle moves in the negative direction at t=2π or 6π.The other parameters are same as in Fig.2

本文曾得到湖南师范大学海文华教授的指导，谨致谢忱.

［1］GOSH P K.Ion traps［M］.Oxford:Clarendon Press，1995.

［2］HAFFNER H，ROOS C F，BLATT R.Quantum computing with trapped ions［J］.Phys Rep，2008，469(4):155-203.

［3］BLATT R，WINELAND D.Entangled states of trapped atomic ions［J］.Nature，2008，453(7198):1008-1015.

［4］陈文钦，海文华，李 辉，等.脉冲式棘齿势场作用下囚禁离子的规则与混沌运动［J］.物理学报，2007，56(3):1305-1312.

［5］LIGNIER H，SIAS C，CIAMPINI D，et al.Dynamical control of matter-wave tunneling in periodic potentials［J］.Phys Rev Lett，2007，99(22):2204031-2204034.

［6］LEIBFRIED D，BLATT R，MONROE C，et al.Quantum dynamics of single trapped ions［J］.Rev Mod Phys，2003，75(1):281-324.

［7］CHEN Q，HAI K，HAI W H.Quantum control of a Paul-trapped ion via double radio-frequency driving［J］.J Phys A Math Theor，2010，43(45):4553021-45530213.

［8］NIE Z X，FENG M，LI J M，et al.Effect of the double frequency of trap field in a Paul trap［J］.Commun Theor Phys，2001，36(11):593-596.

［9］DUNLAP D H，KENKRE V M.Dynamic localization of a charged particle moving under the influence of an electric field［J］.Phys Rev B，1986，34(6):3625-3633.

［10］HUSIMI K.Miscellanea in elementary quantum mechanics-Ⅱ［J］.Prog Theor Phys，1953，9(4):381-402.

［11］HAI W H，HUANG S，GAO K.Wavepacket trains of a Paul trapped ion［J］.J Phys B At Mo Opt Phys，2003，36(14):3055-3061.

［12］HAI K，HAi W H，CHEN Q.Exact manipulations to Bloch states of a particle in a double cosine potential［J］.Phys Lett A，2007，367(6):445-449.

［13］LU G B，HAI W H，XIE Q T.Controlling quantum motions of a trapped and driven electron:an exact analytic treatment［J］.J Phys A Math Gen，2006，39(2):401-405.

［14］曾谨言.量子力学导论［M］.2 版.北京:北京大学出版社，1998.

［15］ZUDOV M A，DU R R，PFEIFFER L N，et al.Evidence for a new dissipationless effect in 2D electronic transport［J］.Phys Rev Lett，2003，90(4):0468071-0468074.

［16］ZHANG W，ZUDOV M A，PFEIFFER L N，et al.Resistance oscillations in two-dimensional electron systems induced by both ac and dc fields［J］.Phys Rev Lett，2007，98(10):1068041-1068044.