基于微机电技术的硅基射频电感的设计与仿真*

章白瑜，高建军* ，闫 娜

(1.华东师范大学信息科学技术学院，上海200241;2.上海微系统所传感技术国家重点实验室，上海200050;3.复旦大学微电子研究院ASCI 国家重点实验室，上海200433)

随着信息技术的发展，射频电路的小型化、集成化已经成为趋势，迫切需要一些低功耗、小体积、易集成的新型元器件［1］。以电感为代表的一系列片外分立元件也是系统中不可或缺的组成部分，而它们的体积问题正成为限制系统尺寸进一步缩小的瓶颈［2］。传统工艺已经越来越难以满足现代射频元件的要求，而MEMS 技术有望解决这个问题。

MEMS(Micro－Electro－Mechanical Systems)指的是可批量制作的，集微型机构、微型传感器、微型执行器以及信号处理和控制电路、接口、通信和电源等于一体的微型器件或系统。相对于传统工艺来说，利用MEMS 技术制作的器件或系统具有以下优点:(1)体积大大减小，便于集成;(2)性能、可靠性大幅度上升;(3)功耗大幅度降低［3］。MEMS 技术的制作工艺通常包括UV－LIGA(远紫外光电铸)、干法刻蚀技术、抛光和电镀技术等［3］。

制作高品质因数无源器件是射频集成电路设计和制作过程中首先需要解决的问题。而螺旋电感由于其结构的特殊性，一直是最难集成的无源器件之一［4］。因此，在MEMS 技术下实现高品质因数的电感设计，对于实现射频电路的集成化、可靠化设计具有极大的现实意义。

用MEMS 技术制作的立体电感由于“悬浮”在基底上方的空气中，不直接和基底接触，寄生电容和寄生电感带来的寄生损耗明显降低，从而可以显著提高电感的品质因数，优化电感性能。这些特点使得MEMS 立体电感具备了优于传统电感的一系列特性，从而能更好地适应现代无线通信技术的需求［5］。因此，MEMS 立体电感具有广阔的应用前景。

1 理论模型和原理分析

螺旋电感常用的理论模型有3 种:1－π 模型［6－12］，2－π 模型［13－17］和T 模型［18－20］。

1.1 螺旋电感的理论模型

1.1.1 1－π 模型

图1 给出了斯坦福大学C. Patrick Yue 在1998年首次提出的螺旋电感两端口1－π 等效模型，该模型由9 个元件组成。

图1 螺旋电感1－π 模型

图1中Cs表示电感线圈间的电容，Rs和Ls分别表示电感线圈的串联电阻和串联电感，Cox1和Cox2表示电感线圈和衬底之间的寄生电容，Csub1、Csub2和Rsub1、Rsub2则分别表示衬底本身的电容和电阻。下面给出上述各参数的计算公式［17］:

其中，l 为电感线圈金属线的长度，ρ 为金属的电导率，W 为线圈宽度，t 为线圈厚度，δ 为趋肤深度，n为线圈匝数，tox为氧化层的厚度，εox为氧化层的介电常数，Cd为衬底单位面积上的电容，Gd为衬底单位面积上的电导。

该模型能够较为准确地描述电感在第1 谐振频率点之前的特性，但由于未考虑趋肤效应和邻近效应，因此在高频有一定误差。因此，文献［7］提出了另一种改进的1－π 模型，如图2 所示。其中，Ls0和Rs0表征串联电感和电阻。Ls1和Rs1串联然后与Rs0并联。这种电路结构用来表征高频时由趋肤效应和邻近效应引起的串联电阻增加。

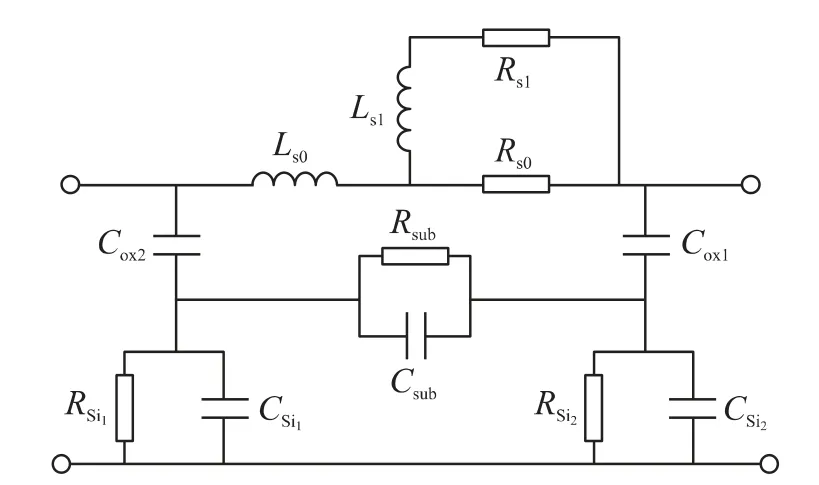
图2 文献［7］中的1－π 模型

1.1.2 2－π 模型

由于1－π 模型没有考虑趋肤效应、临近效应和衬底耦合效应等的影响，更为精确的2－π 模型被提出。由图3 可以看出2－π 模型看作是由两个1－π电路级联而成的，其中C0表示电感线圈间的电容，Rs和Ls表示电感线圈的串联电阻和串联电感，Cp表示下层引出线和螺旋线圈之间的交叠电容。中间接地支路(由COX3、Rsub3和Csub3构成)将整个电路分成相对独立的两个部分，值得注意的是2－π 模型在自谐振频率以上存在一个奇点(Singular Point)，这个奇点往往会导致较大的拟合误差。这也是2－π模型区别于1－π 和T 模型的一个重要特点。

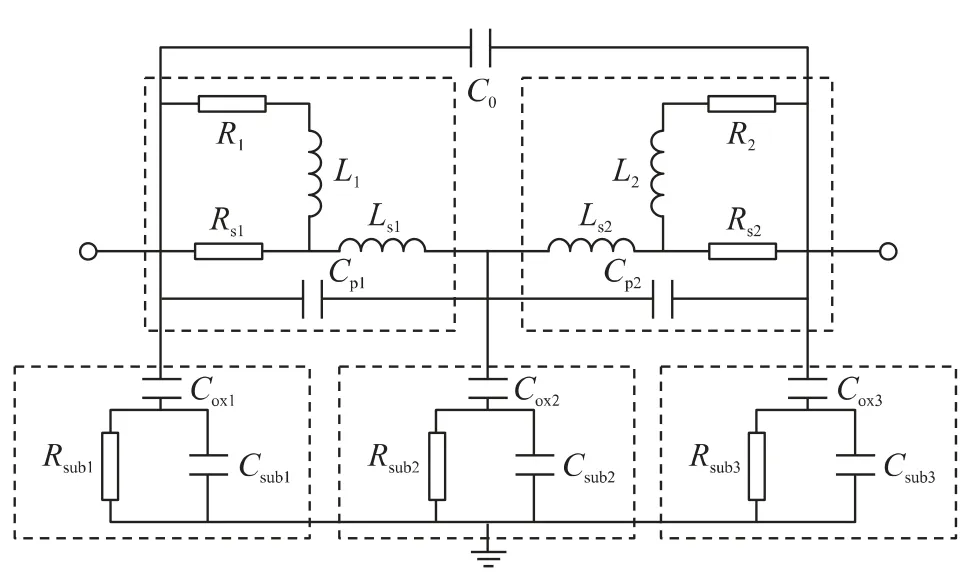
图3 文献［14］提出的非对称2－π 模型

1.1.3 T 模型

图4 所示是J. C. Guo 等人提出的T 模型拓扑结构图。该模型用Rloss、Rsub、Lsub、Csub来表示衬底损耗、电感线圈的损耗。同时，该模型用电阻Rp来表示由衬底损耗回路引起的电感线圈的导体损耗，这样做可以使模型更准确地表示品质因数Q 的峰值。

图4 文献［18］提出的T 模型

1.1.4 模型对比

表1 总结了上述三种模型的优缺点，表2 给出了几种不同的1－π 模型，2－π 模型和T 模型等效电路模型的特征对比，其中“√”代表模型已考虑该效应，“×”代表模型未考虑该效应。

表1 三种电感模型的优缺点比较

表2 片上螺旋电感等效电路模型关键特征对比

1.2 电感品质因数Q 值的理论计算模型

图1 所示的电感理论模型在单端接地的条件下，可以通过电路等效变换得到如图5 所示的等效电路模型。

图5 1－π 模型经过等效变换的电路模型

其中［21］:

Q 值定义式为:

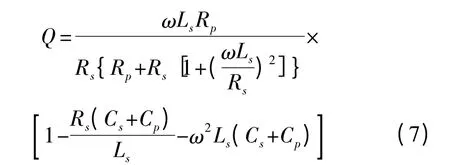
从式(7)可以看出，电感的品质因数Q 是由等式右边的3 个因式所决定的。其中，第1 个因式表征电感线圈所存储的磁场能以及线圈本身的欧姆损耗;第2 个因式表征电感衬底上的能量损耗;第3 个因式是自谐振因子，表示频率上升时，电场峰值能也会随之上升，从而将导致Q 值下降。

在使用HFSS 软件仿真分析电感时，是把电感看作一个二端口元件，计算Q 值的公式为:

2 电感仿真分析

本文设计了两种不同的MEMS 立体电感:第1 种MEMS 立体电感模型为矩形线圈立体电感(如图6 所示)，第2 种MEMS 立体电感模型为立式矩形线圈立体电感(如图7 所示)。以上两种设计均运用终端驱动(Driven Terminal)求解，所设计电感采用半导体硅材料衬底，用介电常数为2.7 的二氧化硅作为介质层。线圈采用电导率较大的铜导线绕制而成，线宽为15 μm，线圈厚度2 μm，线间距1.5 μm，匝数为2.5 匝，不同平面的金属导线之间通过过孔连接。第1 种MEMS 电感线圈平面与衬底之间用h=10 μm 的支柱支撑，形成立体结构。设置该电感端口激励类型为集总端口激励。第2 种MEMS 电感线圈采用立式结构，使整个线圈处于XZ 平面上。线圈平面与衬底之间用支柱支撑，使得线圈底导线与衬底之间的高度差h=10 μm。设置该电感端口激励类型为集总端口激励。

图6 矩形立体电感模型

图7 立式矩形立体电感模型

本文设计的电感制作工艺流程如下:(1)采用N型硅(100)作为衬底材料，电阻率为100 Ω·cm，衬底厚度为300 μm;(2)在硅衬底上进行热氧化，生长厚度为9.8 μm 的SiO2绝缘层;(3)光刻Cu 线圈电镀窗口，厚度约为3 μm，光刻胶为正胶AZ4620;(4)电镀Cu 线圈，厚度为2 μm;(5)用丙酮除去光刻胶，清洗后得到电感。

2.1 矩形线圈立体电感参数分析

图8 是本文设计的矩形线圈立体电感在HFSS中经过仿真运算后得到的矩形线圈立体电感S11和S21参数曲线。当频率为0.1 GHz 时，S11最小，最小值约为－31.32 dB;当频率为18.80 GHz 时，S11有最大值约为－0.82 dB。而随着扫描频率的增大，S11有继续增大的趋势。而对于S21，当频率为0.1 GHz 时，有最大值，趋近0 dB;在0 ～19.80 GHz 扫频内，S21的值单调递减;当频率为19.80 GHz 时，S21达到最小值约为－44.97 dB。图9 是本文设计的矩形线圈立体电感在HFSS 中经过仿真运算后得到的矩形线圈立体电感的L 值曲线。矩形线圈立体电感的L11曲线在0 ～12.90 GHz 范围内基本保持一条直线，在12.90 GHz ～15.50 GHz 以指数形式急速上升。而在扫描频率为15.50 GHz 和15.60 GHz 处出现脉冲似的跳变，此后电感跳变为负值，即在15.50 GHz 处达到谐振点。图10 是本文设计的矩形线圈立体电感在HFSS 中经过仿真运算后得到的矩形线圈立体电感Q 值参数曲线。在频率为4.30 GHz 和4.40 GHz 时，Q11和Q22分别达到最大值，分别为10.99和11.83。

图8 矩形线圈立体电感S11和S21参数曲线

图9 矩形线圈立体电感L 值曲线

图10 矩形线圈立体电感Q 值曲线

2.2 立式矩形线圈电感参数分析

图11 是本文设计的立式矩形线圈立体电感在HFSS 中经过仿真运算后得到的立式矩形线圈立体电感S11和S21参数曲线。在0 ～20 GHz 的扫频曲线中，当频率为0. 1 GHz 时，S11最小，最小值约为－34.11 dB;当频率为16.80 GHz 时，S11有最大值约为－0.30 dB。而随着扫描频率的继续增大，S11减小。而对于S21，当频率为0.1 GHz 时，有最大值，趋近0 dB;在0 ～17.30 GHz 扫频内，S21的值单调递减;当频率为17.30 GHz 时，S21达到最小值约为－44.22 dB，当频率大于17. 30 GHz 时，S21的值有持续增大的趋势。图12 是本文设计的立式矩形线圈立体电感在HFSS中经过仿真运算后得到的立式矩形线圈立体电感的L 值曲线。立式矩形线圈立体电感的L11曲线在0 ～8.90 GHz 范围内基本保持一条直线，在8.90 GHz ～13.50 GHz 以指数形式急速上升。而在扫描频率为13.50 GHz 和13.60 GHz 处出现脉冲似的跳变，此后电感跳变为负值，即在13.60 GHz 处达到谐振点。图13 是本文设计的矩形线圈立体电感在HFSS 中经过仿真运算后得到的矩形线圈立体电感品质因数Q值参数曲线。在频率为4.30 GHz 和4.20 GHz 时，Q11和Q22分别达到最大值，分别为19.51 和19.12。

图11 立式矩形线圈立体电感S11、S21参数曲线

图12 立式矩形线圈立体电感L 值曲线

图13 立式矩形线圈立体电感Q 值曲线

3 矩形线圈立体电感的参数对比

影响电感性能的参数还有线圈宽度、线圈间距、线圈匝数等。本节内容旨在分析不同线圈宽度、线圈间距、线圈匝数的矩形线圈立体电感，研究这些参数的改变对电感性能的影响。

本实验设计了4 种不同线圈宽度的电感，分别为5 μm、10 μm、15 μm、20 μm。实验保持线圈间距1.5 μm，线圈匝数2.5 匝和线圈平面高度10 μm 不变，通过HFSS 进行仿真运算，记录了线圈宽度改变对电感Q 值、L 值、电阻值和自谐振频率的影响。实验结果如表3 所示。

表3 不同导线宽度电感的参数对比

本实验设计了4 种不同线圈间距的电感，分别为1.5 μm、4 μm、6.5 μm 和9 μm。实验保持线圈宽度15 μm，线圈匝数2.5 匝和线圈平面高度10 μm 不变，通过HFSS 进行仿真运算，记录了线圈宽度改变对电感Q 值、L 值、电阻值和自谐振频率的影响。实验结果如表4 所示。

表4 不同导线间隔电感的参数对比

本实验设计了3 种不同线圈匝数的电感，分别为2.5 匝、3.5 匝和4.5 匝。实验保持线圈宽度15 μm，线圈间距1.5 μm 和线圈平面高度10 μm 不变，通过HFSS 进行仿真运算，记录了线圈宽度改变对电感Q 值、L 值、电阻值和自谐振频率的影响。实验结果如表5 所示。

表5 不同导线匝数电感的参数对比

4 结论

本文设计了两种MEMS 电感并进行参数提取，通过不同导线宽度、间距和匝数的电感对比，可以得出以下结论:

(1)电感的品质因数Q 随着线圈宽度增加有增大趋势，随线圈间距增加有减小趋势，随匝数增加有减小趋势;

(2)Q 值峰值时的电感值L 随线圈宽度增加有减小趋势，随线圈间距增加有减小趋势，随匝数增加有增大趋势;

(3)Q 值峰值时的电阻随线圈宽度增加有减小趋势，随线圈间距增加有减小趋势，随匝数增加有增大趋势;

(4)自谐振频率随线圈宽度增加有增大趋势，随线圈间距增加有增大趋势，随匝数增加有减小趋势。

［1］ Pieters P，Vaesen K，Brabels S，et al.Accurate Modeling of High－Q Spiral Inductors in Thin－Film Multilayer Technology for Wireless Telecommunication Applications ［J］. IEEE Transactions on Microwave Theory and Techniques，2001，49(4):589－599.

［2］ Yang Kai，Yin Wenyan，Shi Jinglin，et al. A Study of on－Chip Stacked Multiloop Spiral Inductors［J］. IEEE Transactions on Electron Devices，2008，55(11):3236－3245.

［3］ Wu Chia－Hsin，Tang Chih－Chun，Liu Shen－Iuan.Analysis of on－Chip Spiral Inductors Using The Distributed Capacitance Model［J］.IEEE Journal of Solid－State Circuits，2003，38(6):1040－1044.

［4］ Bahl Inder J. High－Performance Inductors［J］. IEEE Transactions on Microwave Thoery and Techniques，2001，49(4):654－664.

［5］ Burghartz J，Edelstein D，Soyther M，et al. RF Circuit Design Aspects of Spiral Inductors on Silicon［C］//Solid－State Circuits Conference，Digest of Technical Papers. IEEE International，1998:246－247，443.

［6］ Lee Hwan－Hee，Park Jae－Yeong. Characterization of Fully Embedded RF Inductors in Organic SOP Technology［J］. IEEE Transactions on Advanced Packaging，2009，32(2):491－496.

［7］ Yue C P，Wong S S. Physical Modeling of Spiral Inductors on Silicon［J］.IEEE Transactions on Electron Devices，2000，47(3):560－568.

［8］ Lai I C H，Fujishima M. A New on－Chip Substrate－Coupled Inductor Model Implemented with Scalable Expressions［J］. IEEE Journal of Solid－State Circuits，2006，41(11):2491－2499.

［9］ Chen H H，Zhang H W，Chung S J，et al. Accurate Systematic Model－Parameter Extraction for On－Chip Spiral Inductors［J］.IEEE Transactions on Electron Devices，2008，55(11):3267－3273.

［10］ Su C Y，Chen L P，Chang S J，et al. A Macro Model of Silicon Spiral Inductor［J］.Solid－State Electronics，2002，46:759－767.

［11］ Huang F Y，Lu J X，Jiang D M，et al.A Novel Analytical Approach to Parameter Extraction for on－Chip Spiral Inductors Taking into Account High－Order Parasitic Effect［J］. Solid－State Electronics，2006，50(9－10):1557－1562.

［12］ Fujishima M，Kino J. Accurate Subcircuit Model of An On－Chip Inductor with a New Substrate Network［M］.IEEE VLSl Circuits，Digest of Technical Papers，Sympposium on，2004:376－379.

［13］ Liang C K，Razavi B.Systematic Transistor and Inductor Modeling for Millimeter－Wave Design［J］. IEEE Journal of Solid－State Circuits，2009，44(2):450－457.

［14］ Huang F Y，Lu J X，Jiang N，et al. Frequency－Independent Asymmetric Double－π Equivalent Circuit for on－Chip Spiral Inductors:Physics－Based Modeling and Parameter Extraction［J］.IEEE Journal of Solid－State Circuits，2006，41(10):2272－2283.

［15］ Wang C，Liao H，Li C，et al. A Wideband Predictive‘Double－π’Equivalent－Circuit Model for on－Chip Spiral Inductors［J］. IEEE Transactions on Electron Devices，2009，56(4):609－619.

［16］ Gao W，Yu Z P.Scalable Compact Circuit Model and Synthesis for RF CMOS Spiral Inductors［J］. IEEE Transactions on Microwave Theory and Techniques，2006，54(3):1055－1064.

［17］ Yang K，Yin W Y，Shi J L，et al. A Study of on－Chip Stacked Multiloop Spiral Inductors［J］. IEEE Transactions on Electron Device，2008，55(11):3236－3245.

［18］ Yin W Y，Xie J Y，Kang K，et al.Vertical Topologies of Miniature Multispiral Stacked Inductors［J］.IEEE Transactions on Microwave Theory and Techniques，2008，56(2):475－486.

［19］ Horng T S，Jau J K，Huang C H，et al. Synthesis of a Super Broadband Model for on－Chip Spiral Inductors［C］//IEEE RFIC Symposium，Digest of Papers，2004:453－456.

［20］ Guo J C，Tan T Y. A Broadband and Scalable Model for on－Chip Inductors Incorporating Substrate and Conductor Loss Effects［J］.IEEE Transactions on Electron Devices，2006，53(3):413－421.

［21］ Murphy O H，McCarthy K G，Delabie C J P，et al. Design of Multiple－Metal Stacked Inductors Incorporating an Extanded Physical Model［J］. IEEE Transactions on Microwave Theory and Techniques，2005，53(6):2063－2072.