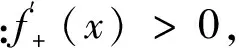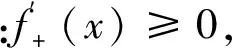可导性缺失情况下函数单调性的研究
2013-12-22欧阳露莎刘敏思
欧阳露莎,刘敏思
(1 中南民族大学 数学与统计学学院,武汉 430074; 2 华中师范大学 数学与统计学学院,武汉 430079)

1 定义及引理
定义1[4-7]设f(x)定义在区间(a,b)内,x∈(a,b),若极限:
,
存在,则称f(x)在x处对称可导(或Schwarz可导),其极限值称为f(x)在x处的对称导数,记为fs(x).若函数f(x)在(a,b)内每一点的对称导数都存在,则称f(x)在(a,b)内对称可导.
定义2 设f(x)在区间I上连续,E⊂I,mE=0,若mf(E)=0,则称E是I中相对于f具有N—性质的集合,简称E相对f具有N—性质,其中mE表示E的Lebesgue测度,f(E)={f(x):x∈E}.
易得,对于区间I上的连续函数f(x),I中总存在相对于f(x)具有N—性质的集合,例如空集,I的至多可数子集等就是这样的集合.

证明对于任意μ∈(f(d),f(c)),记x0=sup{x∈[c,d]|f(x)≥μ},显然x0 事实上,假设f(x0)>μ,则f(x0)>μ>f(d),由连续函数的介值性,存在x1∈(x0,d),使得f(x1)=μ,从而x1∈{x∈[c,d]|f(x)≥μ},这与x0=sup{x∈[c,d]|f(x)≥μ}矛盾,故必有f(x0)=μ. 由x0=sup{x∈[c,d]|f(x)≥μ}知,对任意x∈(x0,d),有f(x)<μ,从而对任意x0+Δx∈(x0,d), 所以: 所以,x0∈E.故μ=f(x0)∈f(E),再由μ的任意性,(f(d),f(c))⊂f(E). 引理2 设f(x)在区间I上连续,记E1={x∈(a,b)|fs(x)≤0或fs(x)不存在}⊂I,若c,d∈[a,b](其中c 证明对于任意μ∈(f(d),f(c)),记x0=sup{x∈[c,d]|f(x)≥μ},类似于引理1的方法可得,x0 下证x0∈E1.事实上,由x0=sup{x∈[c,d]|f(x)≥μ}知,对任意x∈(x0,d),有f(x)<μ,再注意到f(c)>μ=f(x0),还有存在rn→0+,使得x0-rn∈{x∈[c,d]|f(x)≥μ}且x0 故fs(x0)≤0或fs(x0)不存在,从而x0∈E1.再由μ的任意性,(f(d),f(c))⊂f(E1). 定义3[8]设f(x)是[a,b]上的函数,若对任意ε>0,恒有δ>0,使得对[a,b]上的任意一组分点 a≤a1 引理3 若函数f(x)在[a,b]上绝对连续,E⊂[a,b],且mE=0,则E相对f一定具有N—性质. E{a,b}⊂G⊂(a,b)且 mG 由连续函数的介值性,我们选ci,di∈[ai,bi],使得f([ai,bi])=[f(ci),f(di)],注意到: 可得: 0≤m*f(E)=m*f(E{a,b})≤m*f(G)≤ 由ε的任意性可知m*f(E)=0,所以mf(E)=0,即E相对f一定具有N—性质. 证明由于f(x)在区间I上连续,我们只须证明I为开区间时,f(x)在I上严格单调递增即可.以下证明都假设I为开区间. 倘若f(x)在I上不严格单调递增,则至少存在两点c,d∈I(c 下面分两种情形来导出矛盾: 10当f(c)>f(d)时,由引理1得,(f(d),f(c))⊂f(E0)⊂f(E),所以: m*f(E)≥f(c)-f(d)>0, 这显然与E相对f具有N—性质矛盾. 20当f(c)=f(d)时, 若f(x)在[c,d]上不恒为常数,则必存在η∈(c,d),使得f(c)=f(d)≠f(η).当f(c)>f(η)时,由引理1得,(f(η),f(c))⊂f(E0)⊂f(E),所以m*f(E)≥f(c)-f(η)>0,这与E相对f具有N—性质矛盾.当f(c) 综合10、20得,对于∀x1,x2∈I,当x1 证明对任意ε>0,作函数F(x)=f(x)+εx,由条件易得,F(x)在I上连续,且在IE上, 由定理1,F(x)在I上严格单调递增,所以对任意x1,x2∈I,x1 f(x1)+εx1=F(x1) 从而让ε→0得,f(x1)≤f(x2),即f(x)在区间I上单调递增. 推论2 设f(x)在区间I上连续,E为I的至多可数子集, 证明因为E为至多可数集,则f(E)必为至多可数集,从而E相对f具有N—性质,所以,由定理1和推论1即得结论. 注:推论2中,当E=∅时,就是文献[2,3]中的结论. 推论3 设f(x)在区间[a,b]上绝对连续,若f′(x)>0 a.e.于[a,b](f′(x)≥0 a .e于[a,b]),则f(x)在区间[a,b]上严格单调递增(单调递增). 证明记E是[a,b]上不满足f′(x)>0的点所成的集,由条件知,mE=0,再由引理3,定理1和推论1即可证明结论成立. 定理2 设f(x)在区间I上连续,E⊂I,且E相对f具有N—性质,若f(x)在IE上满足:fs(x)>0,则f(x)在区间I上严格单调递增. 证明类似于定理1,我们仅证I为开区间的情形. 倘若f(x)在I上不严格单调递增,则至少存在两点c,d∈I(c 记E0={x∈I|fs(x)≤0或fs(x)不存在},由条件知E0⊂E,从而f(E0)⊂f(E). 下面分两种情形来导出矛盾. 10当f(c)>f(d)时,由引理2得,(f(d),f(c))⊂f(E0)⊂f(E),所以: m*f(E)≥f(c)-f(d)>0, 这与E相对f具有N—性质矛盾. 若f(x)在[c,d]上不恒为常数,则必存在η∈(c,d),使得f(c)=f(d)≠f(η).当f(c)>f(η)时,由引理2得,(f(η),f(c))⊂f(E0)⊂f(E),所以m*f(E)≥f(c)-f(η)>0,这也与E相对f具有N—性质矛盾.当f(c) 综合10、20得,对于∀x1,x2∈I,当x1 推论4 设f(x)在区间I上连续,E⊂I,且E相对f具有N—性质,若f(x)在IE上满足:fs(x)≥0,则f(x)在区间I上单调递增. 证明对任意ε>0,作函数F(x)=f(x)+εx,类似于推论1的方法由定理2即可得结论. 推论5 设f(x)在区间I上连续,E为I的至多可数子集, (1)若f(x)在IE上满足:fs(x)>0,则f(x)在区间I上严格单调递增; (2)若f(x)在IE上满足:fs(x)≥0,则f(x)在区间I上单调递增. 证明因为E为至多可数集,则f(E)必为至多可数集,从而E相对f具有N—性质,所以,由定理2和推论4即得结论. 注:推论5中,当E=∅时,就是文献[5,6]中的结论. [1] Apostol T M.数学分析[M].2版.邢富冲,邢 辰,李松洁,译.北京:机械工业出版社,2006:75-81. [2] 唐艳蕾.连续函数单调性与可导性的充分条件[J].忻州师范学院学报,2002,18(3):56. [3] 杨 军.用单侧导数判别函数的单调性[J].四川师范学院学报:自然科学版,2000,21(1):108-109. [4] 邱德华,李水田.函数一致连续的几个充分条件[J].大学数学,2006,23(3):136-138. [5] 陶有德.关于Schwarz导数的注记[J].信阳师范学院学报,2004,17(1):8-10. [6] 刘三阳,于 力.不可微函数单调性的充要条件[J].西安电子科技大学学报,1995,22(1):74-77. [7] Minch R A.Application of symmetric derivatives in mathematical programming[J].Mathematical-Programming,1971,1:307-320. [8] 江泽坚,吴智泉,纪友清.实变函数论[M].3版.北京:高等教育出版社,2007:175-176.

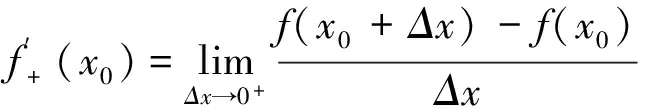

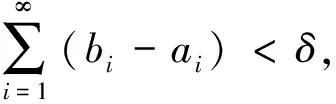
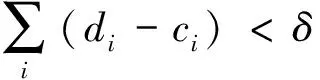



2 主要定理及证明