基于MMP-2DPCA的人脸识别方法

侯建华，牟海军，罗 艳，江小平

(中南民族大学 电子信息工程学院，武汉 430074)

随着科学技术的迅猛发展， 生物特征识别已经成为了安全验证的主要方式，主要是指利用人体的生理特征和行为特征来进行身份的鉴定，包括指纹、人脸、虹膜、笔迹、步态、语音等[1].而在这些众多的生物特征识别当中，人脸识别一直是生物识别领域的研究热点，是一种重要的生物特征识别技术，在自动化身份识别中变得越加的重要[2-4].而所谓的人脸识别，即就是通过已有的若干已知身份的人脸数据库，验证和鉴别给定场景下静态图像或视频中单个或多个人的身份[5].因其具有使用方便、不易仿冒、操作简单、不具侵犯性、直接、友好等优越性，使其在公司考勤、刑事侦查、出入境关口管理、机场检查等领域具有广泛的应用前景.

经过数十年的研究，人脸识别在约束环境下(如人脸表情及姿态确定、无遮挡、光照条件适宜等)取得了巨大的成功[6]，主要包括线性鉴别分析(LDA)、主成分分析(PCA)、独立分量分析(ICA)等.线性鉴别分析[7]以样本可分性为目标使得样本类间离散度与类内离散度比值最大，但在小样本情况下不足以描述人脸变化；主成分分析[8,9]方法通过线性变换找到在最小均方意义下最能代表原始人脸图像的正交基，使得图像数据从高维空间降维到低维空间，不仅能够有效表征原始人脸，而且大大降低了计算复杂度； 独立成分分析[10]方法是基于所有阶统计意义下的去相关，它的计算复杂度要高于主成分分析方法，且在识别率上没有优势.但是在非约束环境下，由于光照条件、遮挡[11]、表情姿态、所处环境等因素的影响，使得人脸图像特征空间变得更加的复杂，进而严重影响了传统算法的识别精度，造成识别困难.

传统的降维方法都是将二维图像转换为一维向量后再寻找最优投影矩阵，然而由于转换后的一维向量维数很高而样本数少，使得求解协方差矩阵的特征值和特征向量很困难.在传统算法的基础上，文献[12-16]提出了使用2DPCA和2DLDA提取人脸特征，其方法为通过直接对人脸图像矩阵形式进行处理，得到了较好的识别效果.

W. Zhao等人将通过对静止图像进行的人脸识别划分为基于全局信息、局部特征和综合方法三种[17].采用全局特征进行人脸识别，是指静止图像中整个人脸区域作为人脸识别系统的初始输入，采用全局特征进行人脸识别的方法中较为典型的就是特征脸和Fisher脸方法；基于局部特征的识别方法是将显著器官(如眼睛、鼻子、嘴)提取出来，然后根据提取出来的局部特征进行几何分析或统计分析，并将其所得到的结果作为结构化分类器的输入；综合方法的出现是由于基于全局特征的人脸表达对于光照、姿态、表情等因素的影响较为敏感,以及局部特征反映的是人脸图像的局部区域，侧重于提取人脸的细节特征，对于光照、表情、姿态和遮挡等变化不敏感，因此结合全局和局部特征信息[18]来识别人脸被越来越多的应用到人脸识别中.通过全局和局部特征的融合，进一步加强了图像的表征能力，这种方法相比于前两种方法在人脸识别中具有更加优越的性能.

基于以上分析，本文提出一种基于二维小波分解和融合多特征主元分析(MMP-2DPCA)的人脸识别方法.由于本文算法融合了人脸的全局特征和局部特征，使其对于人脸图像的光照、表情、遮挡等因素不敏感，对于人脸具有更好的表达能力，从而使得识别结果大大优于单独使用全局特征或局部特征对人脸的识别效果，对人脸具有更好的表达和判别能力，大大的提高了识别率和鲁棒性.

本文在ORL(Olivetti Research Laboratory)人脸数据库上实验，结果表明本文所提出的算法对于人脸具有更好的表达能力，同时也是一种稳定、快速的特征提取和识别方法.

1 二维小波分解的特点

设{Vi}给出了L2(R)的一个多分辨分析，Wi是Vi+1中Vi的补空间，则：

Vi+1=Vi+Wi,

(1)

其中:

(2)

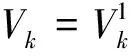
任意给定的f(x,y)∈L2(R2)，fN(x,y)是f(x,y)在空间VN中的投影.这时对fk(x,y)∈Vk与gk(x,y)∈Wk，则有：

fk+1(x,y)=fk(x,y)+gk(x,y),

(3)

而gk(x,y)∈Wk还可以进一步分解为：

(4)

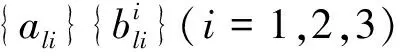
(5)

记:

(6)

此时，分解算法为：

(7)

图1是图像分解的示意图，其中的L表示低频，H表示高频，下标1,2分别表示一级或二级分解.在一个级别的分解的数据传递示意图如图2所示.

图1 图像的小波分解示意图

图2 小波分解数据流示意图

小波变换的一个重要性质就是它在频域和时域都具有很好的局部化特征，同时提供了目标信号在各个频率子段的信息，这种信息对于信号分类是非要有用的.但是如果我们直接对原图降低数据量，仅仅考虑了时域信息，忽略掉了用于有效分类的频域信息.

由于实验中的原图大小是112×96的灰度图，如果在实验中直接对原始人脸图片进行处理，由于原始图像较多的反映了面部的局部细节信息，其中包含了较多的光照、遮罩、旋转扭曲和面部表情等局部细节信息，这些信息体现了模式类内的变化，对人脸鉴别来说是不利的，同时如此大的数据量往往会耗费很长的处理时间.而二维小波分解具有快速、抗干扰、保持图像的大量特征信息，同时对人脸面部表情变化的不敏感性.因此，首先使用二维小波分解对原始图像进行预处理，既保留了面部的全局形状信息，同时又淡化了局部细节，也降低所需要处理的数据量，从而减少了处理时间.

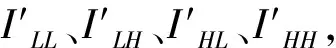
图3 二维小波分解

2 2DPCA原理

设u表示n维单位化的列向量,A为m×n的图像矩阵，A投影到u上，则：

Y=Au,

(8)

即可得到一个m维列投影向量y,称之为图像A的投影特征向量，为了获取到一个最优投影轴,可以使用投影向量的总的散布矩阵,即投影特征向量的散布矩阵的迹.所以定义准则函数：

J(u)=tr(Su),

(9)

其中Su是投影特征向量的散布矩阵,记为：

Su=E(y-Ey)(y-EY)T=
E[Au-E(Au)][Au-E(Au)]T=
E[(A-EA)u)][A-EA)u]T，

(10)

(10)式中,表示计算期望,因此有：

Ju=tr(Su)=uT[E(A-EA)]T(A-EA)]u,

(11)

(12)

我们进一步将所有的图像中心化，则：

(13)

所以J(u)=tr(Su)简化为：

J(u)=uTGu.

(14)

为使图像矩阵在u上投影后得到的特征向量的分散程度最大,采用最大化该准则函数的单位向量,并将其称之为最优投影向量,其中图像总体散布矩阵G的最大特征所对应的单位特征向量对应于最优投影向量. 我们需要找一组满足标准正交条件且极大化准则函数的最优投影向量u1,u2,…，up,其中最优投影向量组u1,u2,…，up是G的对应于前p个最大特征值的正交特征向量. 令U=[u1,u2,…，up],U称为最优投影矩阵. 2DPCA特征提取过程为Y=Au,Y=[y1,y2,…，yp].

3 本文算法

鉴于2DPCA在人脸特征提取方面的不足，本文提出一种新的MMP-2DPCA人脸识别方法，融合人脸的全局特征和局部特征来表征人脸，使得对于人脸具有更好的表达能力.但是如果直接对原始人脸采用MMP-2DPCA算法，不仅仅受到光照、姿态、表情等因素的影响，同时不可避免的需要大量的处理时间，所以在此首先对原始图像进行二维小波分解，分解后的图像既保留了面部的全局形状信息，同时又淡化了局部细节，较原始图像所要处理的数据量也大大降低.

在本文的算法中，我们采用图4的方法来进行全局特征和局部特征的融合.首先对原图进行二维小波分解，将分解得到的低频部分和从原图中提取的人眼、嘴、鼻子进行预处理，之后按照如图4所示的方法进行融合，其中I1为经过二维小波分解的人脸部分，I2，I3，I4分别为眼睛、嘴、鼻子.

图4 全局特征和局部特征的融合

对融合得到的新图像采用2DPCA进行特征提取，最后采用混合马氏距离[19]分类器进行分类识别.在酉空间内，样本y与第i类的混合马氏距离定义如下:

(15)

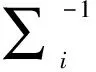
(16)

其中N,Ni,分别表示训练样本总数与第i类的训练样本数，∑表示投影后，训练样本的总体类内协方差矩阵，δ为参数，本文中当δ取值在1/36～1/65之间时，本文算法能够取得最佳识别率95.5 %.

4 实验结果

本文的实验数据取自英国剑桥大学Olivetti研究所制作的ORL人脸数据库.该数据库由40个不同人、每人10幅、共400幅图像组成.这些人的图像是在不同时间、不同视角、不同表情和不同脸节的条件下拍摄的.每幅原始图像有256个灰度级，大小为112×96.实验时，使用每人前5幅图像作为训练样本，后5幅图像作为测试样本.图5给出了ORL人脸库中随机抽取的一个人的人脸图像.

图5 ORL人脸库

为了验证本文所提算法的有效性，分下列三种情况进行研究.

(1)基于局部特征的识别——直接对从原始人脸图像中提取眼睛、鼻子和嘴，将提取的这三个局部特征采用本文所提出的融合方法进行融合，进行基于局部特征的人脸识别.表1给出了各算法的最佳识别率对应的处理时间(整个人脸库上进行训练和分类的时间).

表1 采用局部特征的识别率

(2)基于全局特征的识别——对原始人脸图像和经过二维小波分解后的低频部分分别采用传统的PCA、2DPCA方法，表2给出了各算法的最佳识别率对应的处理时间(整个人脸库上进行训练和分类的时间).

表2 未进行小波分解(上)和进行小波分解(下)的识别率

(3)基于本文算法的识别——分别采用原始人脸图像和经过二维小波分解得到的低频部分作为融合的全局特征，与从原始人脸图像中提取的眼睛、鼻子、嘴的局部特征进行本文所提算法的融合，表3给出了各算法的最佳识别率对应的处理时间(整个人脸库上进行训练和分类的时间).

表3 未进行小波分解(上)和进行小波分解(下)的识别率

表1为基于局部特征方法采用PCA和2DPCA算法的人脸识别结果；表2为基于全局特征采用PCA、2DPCA算法的人脸识别结果；表3为采用本文算法的人脸识别结果.对比基于局部特征、全局特征和本文算法的实验结果可知，采用融合全局特征和局部特征的人脸识别方法，其识别率显然要高于单独采用全局特征或局部特征方法的识别率.

从结果可以看出，直接对原图采用MMP-2DPCA算法相对于采用PCA和2DPCA算法虽然识别率得到了一定的提高，但是却大大的增加了处理时间.经过二维小波分解后虽然直接采用PCA和2DPCA算法耗时少，但是识别率却较低.而经过二维小波分解后采用MMP-2DPCA算法识别率得到了显著的提高，同时和直接采用原图进行MMP-2DPCA算法相比，采用本文提出的算法不仅仅大大的减少了计算时间，同时识别率也得到的显著的提高.

5 结语

本文提出了一种MMP-2DPCA人脸识别算法.该算法首先对原始人脸图像进行二维小波分解，大大降低了原始图像的数据处理量，进而提高了运行速度，然后对分解得到的图像和从原始图像中提取得到的眼睛、鼻子、嘴局部特征进行融合，接着采用2DPCA方法对融合图像进行特征提取，最后采用混合马氏距离进行分类识别.在ORL人脸库上的实验结果表明，本文所提算法与传统的2DPCA算法相比，识别率有着显著的提高的，显示了本文所提算法的有效性.

本文的算法主要是基于二维图像的处理，今后的研究会考虑更多维的特征获取，以提高对于人脸的表达能力，增强鲁棒性.同时也会采用更大的人脸库进行试验，进而提高系统的推广性.

[1] Jain A K,Bolle R,Pankanti S. Biometris: personal identification in networked society[M]. Norwell,USA;Kluwer Academic Publishers,1990.

[2] Clarke R.Human identification in information systems:management challenges and public policy issues[J]. Information Technology & People,1994,7(4):6-37.

[3] Davies S G.ouching big brother:how biometric technology will fuse flesh and machine[J].Information Technology & People,1994,7(4):60-69.

[4] Newham E.The biometric report[R].New York:SJB Services,1995.

[5] Li Stan Z,Jain A. Handbook of face recognition[M].Berlin：Springer,2005.

[6] Zhao W,Chellappa R,Rosenfeld A,et al.Face recognition: a literature survey[J].ACM Computing Surveys,2003,35(4):339-485.

[7] Belhumeur P N,Hespanha J P,Kriegman D J.Eigenfaces vs.fisherface: recogniton using class special linear projection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1997,19(7): 711-720.

[8] Kirby M,Sirovich L. Application of the Karhunen-Loève procedure for the characterization of human faces[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1990,12(1): 103-108.

[9] Turk M,Pentland A. Eigenfaces for recognition[J]. Journal of Cognitive Neuroscience,1991,3(1): 71-86.

[10] Bartlett M S,Lades H M,Sejnowski T J. Independent component representations for face recognition[J]. Proceedings of SPIE,1998,3299(3): 528-539.

[11] Wang Zhiming,Tao Jianhua.Face occlusion detection and reconstruction[J].Journal of Computer Reserarch and Development,2010,47(1):16-22.

[12] Yang J，Zhang D，Frangi A．Two-dimensional PCA: a new approach to appearance-based face representation and recognition[J]．IEEE Transactions on Pattern Analysis and Machine Intelligence，2004：131-137.

[13] Li M．Yuan B．2d-Lda：a statistical linear discriminant analysis for image matrix[J].Pattern Recognition Letters，2005，26(5):527-532.

[14] Qi Y，Zhang J．(2D)2PCALDA：an efficient approach for face recognition[J]．Applied Mathematics and Computation,2009,213(1)：l-7.

[15] Cevikalp H，Yavuz H，Cay M，et al．Two-dimensional subspace classifiers for face recognition[J]．Neurocomputing,2009，72(4-6)：llll-1120.

[16] Du H Sh．Chai X L．Wang F Q，et al．Face recognition using a fusion method based on bidirectional 2DLDA[J]．Chinese Journal of Scientific Instrument，2009，30(9)：1880-1885.

[17] Zhao W,Chellappa R,Phillips P J,et al. Face recognition: A literature survey[J]. ACM Computing Surveys (CSUR),2003,35(4). 399-458.

[18] Su Guangda,Zhang Cuiping,Ding Rong,et al. MMP-PCA face recognition method [J].Electronics Letters,2002,38 (25):1654-1656.

[19] Lawrence S,Yianilos P,Cox I. Face recognition using mixture-distance and raw images[C]//IEEE.IEEE International Conference Systems,Man and Cybernetics.Orlando:IEEE,1997:2016-2021.