随机级数的T-可和性与本性收敛

陈 晨

(1 中南民族大学 数学与统计学学院，武汉 430074；2 湖北大学 应用数学湖北省重点实验室， 武汉 430062)

在分析中当收敛性不成立时会用到广义求和法，广义和的存在性以及和的数值是与相应的求和矩阵紧密相关的，并且我们希望凡是在原求和法下其和存在的级数在新求和法下和仍存在并且两者相等，这种性质为承袭性或者遗传性.文[1]中将这种推广的求和法应用到了随机级数上，并得到随机级数如果几乎必然S-可和，则几乎必然本性收敛.文[2]进一步证明了S求和法具有承袭性以及S-可和性与本性收敛之间是等价的.本文将讨论T求和法是否具有承袭性，以及T-可和性与级数的本性收敛之间的关系，并探讨这种关系是否可以推广到高维空间中.

1 T-可和性

设B为一复Banach空间，{Vm}(m=1,2,…)为B值的向量列.

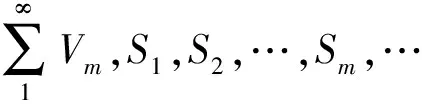
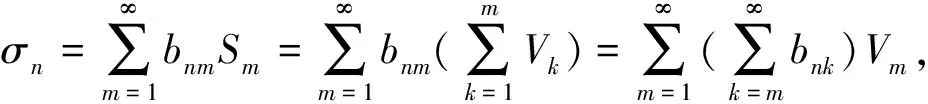
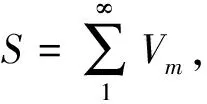
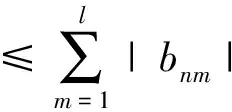
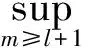
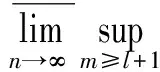
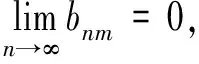
2 T-可和性与本性收敛

证明对于该级数分两种情况讨论：

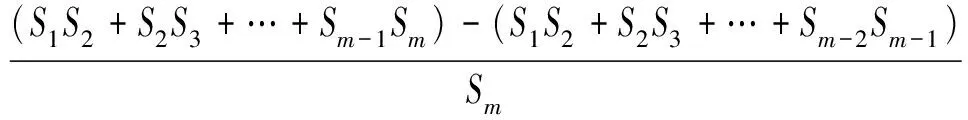
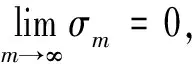
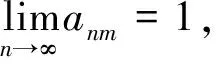
对于美国食品监管机构的监管模式来说，整体设计上按照从上到下的垂直方式来管理。其中，食品方面的部门以监管工作为主，通过食品类别，促使其权责的划分，针对不同类别的食品，实现不同部门的管理。同时，基于食品安全保障体系的应用，也可以将其与政府的监督职能结合，这样在总体上才可以为美国食品安全监管体系提供保障。在各个独立的监管流程中，美国政府颁布了相关法令，各个结构负责执行，并按照法律法规来维护食品的安全性。其中司法部门主要对存在的执法问题进行处理，促使其决策工作更科学，公众也会积极参与其中。在这种情况下，不仅能达到司法、政法与立法之间的独立，在食品安全体系中也将促使其职责的发挥与实现。

注：上述结论(引理1,定理2)同样适用于四元数空间.

下面将上述结论推广到Rn上去.

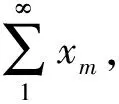
Rn与有限维Banach空间同构，引理4在有限维Banach空间中仍成立，所以易得以下推论2.

最后考虑无穷维B值空间的情形.

证明因为A是相对紧的，所以A中任意无穷序列都含有收敛子列[4].

[1] 卡昂纳 J P.函数项随机级数[M].3版.余家荣，吴 敏，余久曼，译.武汉：武汉大学出版社，1993：12-15.

[2] 陈 晨.随机级数的S-可和性与本性收敛[J].湖北大学学报：自然科学版，2006，28(1)：15-17.

[3] 华东师范大学数学系.数学分析(下册)[M].北京：高等教育出版社，1991：10-11.

[4] 刘培德.泛函分析基础[M].武汉：武汉大学出版社，2002：45-49.

[5] Tian Fanji . A General Fandom Fourier Series[J]. 2002,22(4)：397-401 .

[6] Stiles W J . On subseries convergence in F-spaces[J]. Israel J Math,1970,8:53-56 .

[7] Li Ronglu,Swartz C. Spaces for which the uniform bouned principle holds[J]. Studia Sci Math Hungar,1992,27:379-384.