基于精英蚂蚁算法的动态路由和波长分配研究

孙文胜 ，景勇祥

(杭州电子科技大学通信工程学院，杭州310018)

下一代密集波分复用光网络DWDM(Dense Wavelength Division Multiplexing)将会工作在拥有光分组交换、光波长交换的混合模式中，而实现在混合模式下工作的关键技术之一就是路由和波长分配RWA(Routing and Wavelength Assignment)［1］。在动态路由和波长分配DRWA(Dynamic Routing and Wavelength Assignment)问题中由于连接请求是动态的，因此研究DRWA 问题的目的是如何在减少所需要的波长数的同时降低光路连接请求的阻塞率［2-3］。同时在RWA 问题中还需要注意“波长连续性的限制”和“不同波长的限制”这两个限制条件，这又为解决RWA 问题带来了一定的困难。目前已经有遗传算法、蚁群算法等启发式算法应用到了DRWA 问题中［4-6］。文章将精英策略蚂蚁系统EAS(Elite strategy Ant System)算法应用到DRWA 问题中。通过与最短路径算法和基本蚁群算法进行比较后，可以发现EAS 算法在降低网络阻塞率方面具有明显的优势，当波长数目增多或者网络负载增加时这种优势更加明显，能有效提高DWDM 光网络中带宽资源利用率。

1 EAS 算法模型

蚁群算法应按是一种受真实的蚂蚁行为启发的新型模拟进化算法［7-9］。而精英策略蚂蚁系统算法(EAS)是对基本蚂蚁算法的改进，它的思想是在基本蚂蚁系统算法的基础上，对到目前为止找到的最优路径实施一种精英策略，得到额外反馈信息的蚂蚁将更加容易找到最优路径［10］。

1.1 路径的构建

每一只蚂蚁都使用逐步决策方法从源点开始建立问题的解。在每一个结点上，蚂蚁都会读取存储在结点上的局部信息，并根据路径(i，j)在t 时刻的信息素τij来选择移动到哪一个结点。本文将所有边上的信息素都固定为1，即τij=1，∀(i，j)∈A，ηij为路径(i，j)的启发式信息，其一般为dij的倒数，dij为路径(i，j)的长度，α 和β 分别代表信息素和启发式信息的相对影响力。假设蚂蚁k 在t 时刻的转移概率)为:

式中，U 为可行顶点集。当α=0 时，此时EAS 算法相当于经典的随机贪心算法;而当β=0 时，此时只有信息素在起作用，而没有利用任何启发式信息带来的偏向性，这将使得算法很快地陷入停滞的状态，此时所有的蚂蚁将按照同一条路线移动，最后构建出同一条路径。目前构建到的最优路径即为Tbs。

1.2 信息素的更新

当蚂蚁到达目的结点后，它就会从正向模式转换为逆向模式，各边上的信息素将会随着蚂蚁沿着原路径返回时被更新。假设蚂蚁k 在路径(i，j)上释放的信息素数量为，任意一条边的路径长度均设定为1，信息素的挥发度为ρ(0≤ρ≤1)。参数ρ 的作用是避免信息素的无限积累，而且还可以使算法“忘记”之前较差的路径。事实上，如果一条边没有被任何一条蚂蚁选择，那么这条边的信息素将会以迭代次数的指数级递减。而针对路径Tbs的格外强化是通过向Tbs中每一条边增加e/Cbs大小的信息素，其中e 定义了给予路径Tbs的权值大小，本文将其定义为e=16，而Cbs代表了Tbs的路径长度。

这样，信息素的更新规则就变为:

设CK为第k 只蚂蚁在本次循环中所走的路径长度，Q 表示一只蚂蚁经过一次循环后代表的所有信息，为一固定常数，文中选定Q 为常数1，则:

可以发现蚂蚁构建的路径越好，那么路径上的各条边就会获得更多的信息素，从而在蚂蚁最终选路的过程中寻找到最短路径。

2 EAS 算法与DRWA 问题结合和实现

考虑到“波长连续性的限制”和“不同波长的限制”的限制，本文DWDM 光网络以包交换的形式工作，网络拓扑也提前预知，并设定DWDM 网络中的每一个结点都具有相同的波长数目，且各个结点不具有波长转换功能。

在仿真中使用了典型的美国国家科学基金会网络NSFNET(National Science Foundation Network)，该网络的拓扑具有14 个结点和21 个连接数，如图1 所示。

图1 拥有14 个结点、21 个连接数的虚拟网络的拓扑图

2.1 路径的构建和路由表的更新

为了利用蚂蚁能根据信息素来进行路由选择，网络中的每个结点的路由表用信息素表来代替。信息素表中的信息素浓度以概率值的形式来表示，这样的选择路由的方式与蚂蚁根据信息素多少选择路径具有本质上的一致性。为了支持动态路由选择，一个拥有ki个邻结点的结点i 拥有路由表该路由表具有N-1 行、ki列，每一行对应的是目的结点，每一列对应的是邻结点，其中N 为结点个数。在路由表中代表的是一个蚂蚁在寻找目的节点d 的过程中选择n 作为下一跳的可能性，这个概率也就是前面所提到的蚂蚁k 在t 时刻的转移概率为NSF 网络中结点5 的路由表如表1 所示。

表1 NSF 网络中结点5 的路由表

当源结点为5 和目的节点13 时并且连接请求到来时，邻结点9 将会被选为下一跳的结点，因为通过概率比较可以明显得到

同时对于任一的一个目的节点，始终满足这样一个规律:所有的邻结点都必须满足相加总和为1，也就是每行元素相加都为1，即:

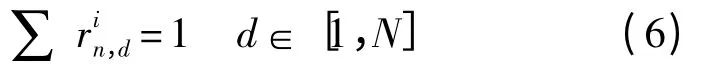
对于路由表的更新，当蚂蚁到达目的结点之后，它就会从正向模式改为逆向模式，然后一步一步地按原路返回到源结点处。在蚂蚁开始返回之前，会先消除在向目的结点寻找过程中所经过路径上的环路，以此来优化路径。在返回过程中，蚂蚁通过释放大小为Δτ的信息素，来改变转移概率，最终完成对路由表的更新。

EAS 算法的工作流程如图2 所示。

图2 EAS 算法的工作流程图

2.2 数据包的传输和更新

蚂蚁在寻找最短路径的过程中，它会采集两种信息:路径的长度和拥塞信息。每一个“蚂蚁”(即数据包)携带以下的信息:源结点、目的结点、二进制码序列M、阻塞信息、路径信息和TTL。

由于每一个结点有拥有相同的波长数目，因此该文用1 个二进制码序列m 来一一对应结点中的各个波长，其中0 表示该波长不可用，1 表示该波长可用。而每一个蚂蚁携带的二进制码序列M 反应的是经过之前结点后各个波长的使用状态，其中0也表示某波长不可用，1 表示该波长可用。然后将数据包M 和结点m 进行“与”运算，那么就可以得到最新的波长使用情况。

假如在WDM 网络中拥有5 个波长800 nm、900 nm、1 000 nm、1 100 nm、1 200 nm。在某结点假如只有1 000 nm 和1 200 nm 可用，那么二进制码序列M1结点则为00101，而蚂蚁携带的数据包中的二进制序列M1中为900 nm 和1 200 nm 可用，其二进制码序列为01001，那么将二者进行与运算以后，可以得到更新后的M1为00001，即只剩下1 200 nm 波长可用，如表2 所示。

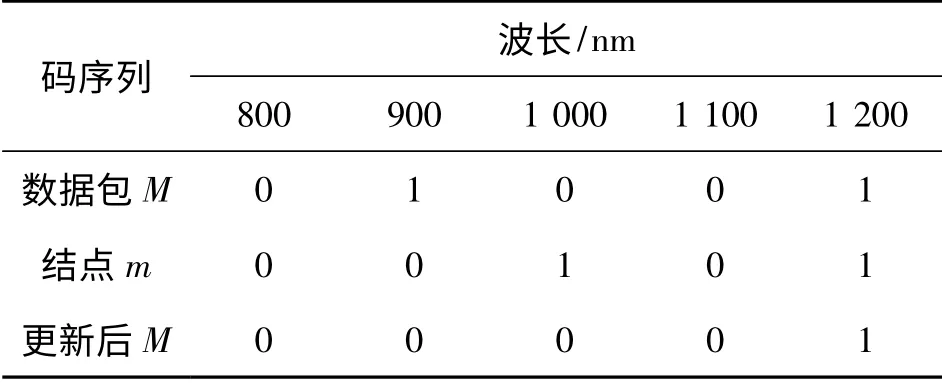
表2 波长使用情况

路径信息中不仅包含经过路径的长度，还包括该蚂蚁所经过的所有结点名称。在算法中，当蚂蚁到达其目的节点或者无法为新路径寻找到一个可分配的波长的时候，蚂蚁将会被杀死，以此避免对网络造成拥塞。同时还设置了一个生存时间TTL，每经过一个结点，其TTL 减少1，当TTL 减少为0 时，蚂蚁将被杀死，以此提高算法的运算效率。

在EAS 算法中，还加入了一个判断机制，用来避免当多次找到最优路径后算法迭代次数远远小于最大迭代次数时造成的资源浪费。在蚂蚁找到路径T 后，会将其与之前存储的最优路径Tbs进行对比，在这里、会设置一个计数值P，当蚂蚁寻找到最优路径，计数值P 都会减去1，当P＜0 即认为其已经找到最优路径，算法结束。

3 仿真结果和分析

由于DRWA 问题中，连接数是动态的，因此该文将NSF 网络看成一个话务网络，则其网络负载就可以表示为:

式中话务量A 也就是相当于DWDM 网络的负载，而话务呼叫次数C 也就是DWDM 光网络中的连接请求数目。在仿真中我们将话务持续时间T 固定，取值为5 s，只改变连接请求数目C。

对于DRWA 问题，文献中往往将优化目标选定为最大化网络收益或者最小化网络损失，将优化目标简化为最大化网络的连接数或者最小化网络的拥塞率，本文选择最小化网络的拥塞率。链路中的拥塞率定义为该链路上可用的波长数目与总波长数目之比，即:

那么可用波长数目越多，则该链路的拥塞也就越小。

在仿真中，将各项参数设置如下:信息素影响力α=1，启发式信息β=1，信息素挥发系数ρ=0.5，最优路径影响因子e=16，蚂蚁数目m=25，计算值p=10，最大的迭代次数为50。为了保证数据的可靠性，将每种算法运行20 次，取其阻塞率的平均值。仿真结果如图3 所示。然后，选择负载相同的情况，其仿真结果如图4 所示。对于不同的波长数目，随着波长数目的增多，网络阻塞率都会明显地下降。而当波长数目选择一定的时候EAS 算法都比最短路径路由算法和基本蚁群算法拥有更低的阻塞率，而当波长数目越多时，这种优势越发明显。

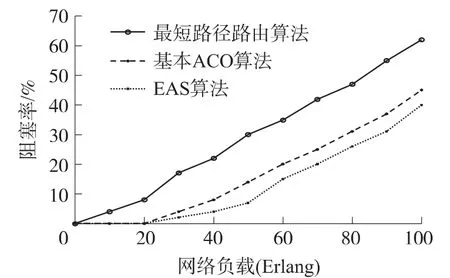
图3 波长数W=16 时3 种算法的阻塞率

图4 负载相同时3 种算法的阻塞率

4 结束语

作为DWDM 光网络中首要解决的DRWA 问题，由于其连接请求的动态性，以及受到DWDM 光网络的两个限制条件的限制，文章将用于模拟自然界蚂蚁寻找最短路径行为的EAS 算法应用到解决DRWA 问题中，可以发现与最短路径路由算法和基本蚁群算法相比，EAS 算法能够更加有效地降低光网络阻塞率，提高网络中带宽资源的利用效率。同时在实验中增加蚁群数目能够提高蚂蚁正确选择最短路径的概率，但同时网络开销也会增大。因此如何处理好蚁群数目和网络开销的动态平衡问题，以及在仿真中对各个参数的选取设定和解决算法计算开销大的诸多问题，这些都有待于以后在算法的改进和实验的验证。

［1］ 付明磊.波长路由光网络中的路由和波长分配算法研究［D］.杭州:浙江工业大学，2007.

［2］ 乐孜纯，张明，全必胜. 光网络实用组网技术［M］. 西安:西安电子科技大学出版社，2008:20-45.

［3］ 张仕俊.WDM 光网络中路由与波长分配算法的研究［J］.杭州电子科技大学学报，2010，26(3):156-158.

［4］ Joan Triay，Cristina Cervello-Pastor. An Ant-Based Algorithm for Distributed Routing and Wavelength Assignment in Dynamic Optical Networks［J］.IEEE Journal on Selected Areas in Communications，2010，28(4):542-552.

［5］ 段海滨. 蚁群算法原理及其应用［M］. 北京:科学出版社，2005.

［6］ 张颖，朱娜，朱士芬. 基于D ～* 思想的动态RWA 算法研究［J］.光通信研究，2007(2):4-7.

［7］ 段亚伟，朱娜，李正茂.基于遗传算法的动态RWA 问题的研究［J］.计算机工程与应用，2005，23:132-134.

［8］ Dorigo M. Heuristic from Nature for Hard Combinatorial Optimization Problems［J］. International Transactions in Operational Research，1996，3(1):1-21.

［9］ 陈旭，宋爱国.蚂蚁算法与免疫算法结合求解TSP 问题［J］.传感技术学报，2006(2):504-507.

［10］ Marco Dorigo，Thomas Stuitizle.Ant Colony Optimization.［M］.北京:清华大学出版社，2007:30-51.