基于有限元分析的石墨烯弹性性能和振动特性

唐文来 彭倚天 倪中华

(东南大学江苏省微纳生物医疗器械设计与制造重点实验室, 南京 211189)

由Novoselov等[1]首先发现石墨烯(又称为二维石墨片),而石墨烯是其他石墨材料的基本单元[2]．实验研究表明，石墨烯的杨氏模量高达1TPa[3],并且具有极高的振动频率[4]．优异的弹性性能和振动特性,使得石墨烯在纳米复合材料、纳米振荡器、纳米传感器和纳米机电系统中有着广阔的应用前景[5-6]．

目前,对石墨烯弹性性能和振动特性的研究方法主要有实验测试、原子模拟和连续介质模拟．Lee等[3]利用原子力显微镜纳米压痕法研究了石墨烯的力学性能,得到石墨烯的杨氏模量为(1.0±0.1)TPa,理想强度为(130±10)GPa．Bunch等[4]构建了石墨烯机电谐振器,检测到谐振器的共振频率达到MHz量级．由于在纳米尺度下进行有效的实验非常困难,研究者尝试通过量子力学和分子动力学等原子模拟方法研究石墨烯．Liu等[7]采用从头计算方法，得到石墨烯的杨氏模量和泊松比分别为1.05TPa和0.186．Gupta等[8]通过分子力学模拟研究了石墨烯的弹性性能和自由振动频率,发现石墨烯的振动频率在THz量级．这些原子模拟方法能够得到较准确的结果,但由于巨大的计算量使其应用受到限制．连续介质模拟方法具有计算效率高、理论简单等特点,在石墨烯研究方面得到了广泛的应用．基于Li等[9]提出的分子结构力学方法,Sakhaee-Pour研究了不同手性石墨烯的弹性性能[10],并分析了手性、尺寸和边界条件对石墨烯振动特性的影响[11]．Shakouri等[12]提出基于REBO势的石墨烯连续介质模型,研究了石墨烯的振动和屈曲行为,发现手性对振动和屈曲行为的影响很小．以上的连续介质方法是通过建立分子力学局部原子势和结构力学单元应变能相等价的关系,确定代替石墨烯微观结构的等效单元参数,方法的准确性很大程度上取决于原子势函数的选取．Shakouri等[12]分别采用AMBER势和REBO势研究了石墨烯的振动特性,发现不同势函数得到的结果并不相同．

本文基于改进的分子结构力学方法[13],采用矩形截面梁单元代替碳-碳共价键,将石墨烯的微观原子结构等效成空间框架结构,建立石墨烯的连续介质模型．通过分析石墨层的典型受载情况确定等效单元参数,避免了原子势函数的选取问题．借助有限元软件,实现石墨烯的参数化建模,分别对模型进行线性静力和模态分析,计算得到石墨烯的弹性常量、固有频率和振型,并系统地讨论了手性、尺寸和边界条件对石墨烯的弹性性能和振动特性的影响．

1 理论与建模

在石墨烯的微观结构中,单层碳原子通过碳-碳键相互结合围成正六边形蜂窝结构[2],如图1(a)所示．根据边缘结构的不同,石墨烯分为扶手椅型和锯齿型2种．石墨烯的正六边形单胞如图1(b)所示,可以看出碳-碳键的作用形式有键的伸长(Uρ)、面内键角变化(Uθ)、离面键角变化(Uω)和二面角扭转(Uτ)．

图1 碳-碳键到梁单元的等效[13]

小变形情况下,碳-碳键4种作用形式对应的势能可用谐和函数来描述,这与梁单元的变形能具有相同的形式,因此可用梁单元代替碳-碳键．采用Li等[13]提出的改进分子结构力学,利用图1(c)所示的矩形截面梁单元等效碳-碳键，将无限大的石墨烯看作石墨层.通过分析石墨层的典型受载情况(单轴拉伸和纯弯曲)可以得到等效梁单元的参数为

(1)

式中,L为长度;A为截面面积;Iy和Iz为截面惯性矩;J为截面极惯性矩;E,G分别为弹性模量和切变模量．等效梁的几何参数和力学参数值都是虚拟的,并不是石墨烯自身的参数,但只要这些参数组合起来满足式(1),就可以实现对碳-碳键的等效．

研究石墨烯的振动特性,还需要考虑碳原子质量的作用．石墨烯结构中,碳原子的质量(mc=1.9943×10-23g)主要集中在原子核上,而原子核的直径非常小(rc=2.7×10-6nm),可以忽略转动惯量的影响,采用集中质量单元来代替碳原子．

利用有限元软件ANSYS的参数化设计语言,在石墨烯结构中碳原子的位置生成节点,在节点上创建集中质量单元(MASS21)代替碳原子,再利用梁单元(BEAM4)连接相邻节点,即可建立石墨烯的框架结构连续介质模型．对模型进行结构线性静力和模态分析,线性静力分析时定义默认的求解选项,模态分析中采用分块兰索斯法,定义模态扩展数为5,其他选项设置为缺省值．

2 结果与讨论

2.1 石墨烯的弹性性能

杨氏模量、剪切模量等弹性常量是属于连续介质框架下的力学概念.石墨烯是由单层碳原子构成,因此须假设其厚度后才能计算出等效的弹性常量．石墨是由石墨烯层层堆叠而成的[2],因此采用石墨的层间距离(0.34nm)作为石墨烯的厚度．

石墨烯由长度a和宽度b来表征,对石墨烯模型进行结构线性静力学分析,单轴拉伸和纯剪切力学分析如图2所示.根据载荷与变形量之间的关系,可得到石墨烯的杨氏模量、泊松比和剪切模量．

图2 石墨烯的静力学分析示意图

石墨烯的单轴拉伸模拟如图2(a)所示,将最底层的节点固定,在最上端的节点上施加位移Δa．拉伸完成后,计算所有固定节点在长度方向上的总反力F,同时得到石墨烯在宽度方向上的变形量Δb,通过下式得到石墨烯的杨氏模量Eg和泊松比μg:

(2)

(3)

式中,σ,ε为拉伸应力和应变;t为石墨烯厚度．

石墨烯的纯剪切模拟如图2(b)所示,将底层节点固定,在最上端和左右两端施加相同的等效切应力τ．根据模型的变形量,通过下式计算石墨烯的剪切模量Gg:

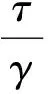
(4)

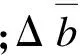
2.1.1 石墨烯的杨氏模量和泊松比

在模拟单轴拉伸时,为了减小两端施加载荷带来的局部影响,取长度a=4b．对2种手性石墨烯进行单轴拉伸模拟,得到杨氏模量和泊松比随宽度的变化曲线如图3(a)和(b)所示．图3(a)中包含将梁单元进行10倍细化网格后得到的结果,比较发现不同网格密度的最大误差在1%左右,因此可以采用单个梁单元来模拟共价键．图3(a)表明,扶手椅型石墨烯的杨氏模量值大于锯齿型,说明杨氏模量与手性相关;随着宽度的增加,扶手椅型石墨烯的杨氏模量急剧减小,而锯齿型则迅速增大,当宽度足够大时(大于10nm),2种手性石墨烯的杨氏模量逐渐稳定,趋于1.03TPa．由图3(b)可知,扶手椅型石墨烯的泊松比小于锯齿型,说明泊松比同样与手性相关;随着宽度的增加,2种手性石墨烯的泊松比都呈下降趋势,当宽度足够大时(大于10nm),2种手性石墨烯的泊松比接近0.175．

图3 弹性常量随尺寸的变化曲线

2.1.2 石墨烯的剪切模量

取a=b,对2种手性石墨烯进行纯剪切模拟,图3(c)给出了剪切模量随边长的变化曲线．从图中可以看出,扶手椅型石墨烯的剪切模量略高于锯齿型,表明手性对剪切模量的影响较小;剪切模量随着边长的增加而逐渐变大,边长较小时上升较快,当边长足够大时(大于10nm)剪切模量趋于440GPa．

由以上分析发现,石墨烯的弹性性能与手性和尺寸都相关．扶手椅型石墨烯具有较大的杨氏模量、剪切模量和较小的泊松比,说明扶手椅型石墨烯的弹性性能优于锯齿型．弹性常量随尺寸有着不同的变化规律,当尺寸足够大(大于10nm)时,石墨烯表现出各向同性,其杨氏模量、剪切模量和泊松比的值分别趋于1.03TPa,440GPa和0.175,这与其他研究者得到的结论一致[3,7,14]．

2.2 石墨烯的振动特性

通过对模型的模态分析,能够得到石墨烯的固有频率和对应振型．石墨烯框架结构模型的无阻尼自由振动方程为

Mü+Ku=0

(5)

取a=b,考虑图4的3种边界条件,研究石墨烯的振动特性．分析边长为10nm的正方形石墨烯,得到振动基频如表1所示.表中包含了采用文献[11-12]方法所得到的振动基频．可以看出,本文的结果与Shakouri等[12]得到的结果基本一致,而文献[12]是通过采用密度泛函方法证明其结果的准确性．

图4 石墨烯的边界条件示意图

表1 不同方法得到的振动基频 GHz

分析边长为20nm的2种手性石墨烯在2端固定时的振动,得到前5阶固有频率如图5(a)所示．图中可以看出,2种手性石墨烯的固有频率基本一致,表明手性对固有频率的影响很小．

图5(b)描述了在2端固定情况下,不同边长扶手椅型石墨烯的前5阶固有频率．由图可知,边长为5nm的石墨烯具有的固有频率远大于其他石墨烯,固有频率随着边长的增大而减小,且当边长较大时,固有频率逐渐稳定,说明尺寸对固有频率的影响很大．

边长为20nm的扶手椅型石墨烯在3种不同边界条件下的固有频率如图5(c)所示．图中可以看出,1端固定、2端固定和4端固定条件下的固有频率依次增加,表明对石墨烯的边界约束越多，得到的固有频率就越大．

图5 不同条件下的固有频率

通过模态扩展可以得到石墨烯固有频率对应的振型,图6(a)比较了边长为20nm的扶手椅型石墨烯,在3种边界条件下的前3阶振型．可见,不同边界条件下的振型是完全不同的,对于1端固定和2端固定的石墨烯而言,最大的振幅发生在自由边界处,而4端固定石墨烯的最大振幅则发生在石墨烯内部,这些现象与已有的研究吻合[12,15]．边长为20nm的2种手性石墨烯在2端固定时的振型如图6(b)所示.图6(c)展示了边长分别为20,30nm的扶手椅型石墨烯在2端固定时的振型．图6(b)和(c)表明,不同手性和不同尺寸下的石墨烯具有的振型相似,表明手性和尺寸对石墨烯振型的影响并不显著．

图6 不同条件下的振型

3 结论

1) 石墨烯的弹性性能与手性和尺寸都相关．扶手椅型石墨烯的弹性性能优于锯齿型,具有较大的杨氏模量、剪切模量和较小的泊松比．石墨烯的弹性常量随尺寸的变化规律不同,但当尺寸足够大时(大于10nm),其杨氏模量、剪切模量和泊松比的值分别趋于1.03TPa,440GPa和0.175,表现出各向同性．

2) 手性对石墨烯振动的固有频率和振型影响很小;石墨烯的固有频率与尺寸和边界条件相关,尺寸越小、边界的约束越多得到的固有频率就越大;尺寸对石墨烯振型的影响不显著,而在不同边界条件下的振型则完全不同．

3) 由于纳米尺度的实验非常复杂,没有对模拟结果进行实验验证,而是通过和已有的研究进行比较来说明结果的正确性．

)

[1]Novoselov K S, Geim A K, Morozov S V, et al. Electric field effect in atomically thin carbon films[J].Science, 2004,306(5696): 666-669.

[2]Geim A K, Novoselov K S. The rise of graphene[J].NatMater, 2007,6(3): 183-191.

[3]Lee C, Wei X D, Kysar J W,et al. Measurement of the elastic properties and intrinsic strength of monolayer graphene[J].Science, 2008,321(5887): 385-388.

[4]Bunch J S, van der Zande A M, Verbridge S S, et al. Electromechanical resonators from graphene sheets[J].Science, 2007,315(5811): 490-493.

[5]Geim A K. Graphene: status and prospects[J].Science, 2009,324(5934): 1530-1534.

[6]Katsnelson M I. Graphene: carbon in two dimensions[J].MaterialsToday, 2006,10(1/2): 20-27.

[7]Liu F, Ming P M, Li J. Ab initio calculation of ideal strength and phonon instability of graphene under tension[J].PhysicalReviewB, 2007,76(6): 064120-1-064120-7.

[8]Gupta S S, Batra R C. Elastic properties and frequencies of free vibrations of single-layer graphene sheets[J].JournalofComputationalandTheoreticalNanoscience, 2010,7(10): 2151-2164.

[9]Li C, Chou T W. A structural mechanics approach for the analysis of carbon nanotubes[J].InternationalJournalofSolidsandStructures, 2003,40(10): 2487-2499.

[10]Sakhaee-Pour A. Elastic properties of single-layered graphene sheet[J].SolidStateCommunications, 2009,149(1/2): 91-95.

[11]Sakhaee-Pour A, Ahmadian M T, Naghdabadi R. Vibrational analysis of single-layered graphene sheets[J].Nanotechnology, 2008,19(8): 085702-1-085702-7.

[12]Shakouri A, Ng T Y, Lin R M. A new REBO potential based atomistic structural model for graphene sheets[J].Nanotechnology, 2011,22(29): 295711-1-295711-8.

[13]Li H J, Guo W L. Transversely isotropic elastic properties of single-walled carbon nanotubes by a rectangular beam model for the C—C bonds[J].JournalofAppliedPhysics, 2008,103(10): 103501-1-103501-11.

[14]Zaeri M M, Ziaei-Rad S, Vahedi A, et al. Mechanical modelling of carbon nanomaterials from nanotubes to buckypaper[J].Carbon, 2010,48(13): 3916-3930.

[15]Garcia-Sanchez D, van der Zande A M, Paulo A S, et al. Imaging mechanical vibrations in suspended graphene sheets[J].NanoLetters, 2008,8(5): 1399-1400.