基于混合型鲁棒输入训练神经网络的非线性数据校正方法及其应用

任少君 司风琪 李欢欢 徐治皋

(东南大学能源热转换及其过程测控教育部重点实验室,南京210096)

随着自动化信息技术在火电机组中的普遍应用,热工过程的监测、控制和诊断分析越来越多地依赖于机组自动控制和信息系统,而过程实时测量数据则是这些系统可靠运行的重要信息基础,其准确性对机组监控有着直接的影响.但是，由于受到各参数测量原理与方法、变送器及仪表精度等多种因素的影响,测量数据往往不能满足反映过程物理规律的平衡方程,传感器故障在测量数据中还可能出现大的异常值,因此必须对所测量数据进行必要的校正处理,相关研究已经引起研究者的重视,并发展了多种数据校正方法[1-4].

在现有数据校正算法中,系统机理模型采用定量解析冗余信息,但是对于热工过程这样的复杂对象,常常难以准确确定一些模型系数,而且由于计算量等方面的限制,经常需要在建模过程中做出各种简化假设处理,从而影响了模型精度,也限制了这类方法的使用[5].人工智能模型和统计特性模型等数据驱动方法是另一类过程建模方法.它们将实际过程看作黑箱对象,以过程输入输出数据为基础建立模型,在数据校正中得到了大量应用,但是该类方法缺少过程先验知识,所建模型往往难以对过程物理规律给出合理的解释[6-7].为此，一些研究者已提出了基于机理特性和神经网络的混合建模方法,通过神经网络对机理模型参数进行辨识,并在过程建模与仿真方面得到了较好的应用[8-10].

本文提出了一种混合型鲁棒输入训练神经网络(hybrid robust input-training neural network,H-RITNN),在原RITNN网络的目标函数中引入了反映过程机理的约束方程,并给出了该网络学习算法,进而提出了基于H-RITNN网络的非线性数据校正方法,给出了数据校正的具体流程.本文还分别针对非线性测试函数和某1 000 MW机组进行了算例分析,以验证本文H-RITNN模型的有效性和准确性.

1 RITNN网络

如图1所示,RITNN网络由输入层、隐层和输出层3部分组成,其中输入层变量作为原始数据降维后的非线性主元,包含了其测量数据中的主要信息,其节点数一般小于输出层节点数,网络输出为原测量数据的估计值[11-13].

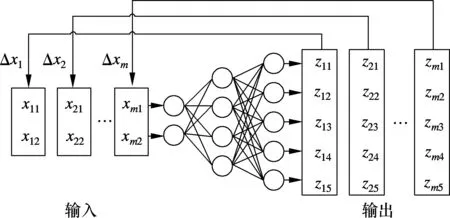
图1 H-RITNN网络结构示意图

采用误差反传梯度下降法进行RITNN网络训练时,对于含有n个变量的m组训练样本数据经标准化处理后得到目标数据集{tpk},1≤p≤m,1≤k≤n.网络训练目标函数为

(1)

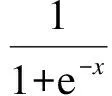
(2)

式中,bj为第j个隐层节点阈值;vij和wjk分别为输入层和隐层之间以及隐层和输出层之间的网络权值,由式(1)对各变量求偏导可得

(3)

(4)

(5)

式中,Δxpi为网络输入值调整量;Δvij和Δwjk为网络内部权值调整量.

RITNN网络通过训练可确定各个连接权值,与其他前向神经网络不同,网络测试时还需要对网络输入值进行调整,其目标函数Eg为

(6)

网络测试输入调整值为[11]

(7)

2 H-RITNN网络

2.1 网络建模

根据所研究对象的过程机理,测量数据需要满足一定的约束方程,RITNN的网络输出也必须满足该约束条件[14],常见约束方程为

fl(x,v,w)=0l=1,2,…,l0

(8)

gd(x,v,w)<0d=1,2,…,d0

(9)

则对网络的训练问题可描述为

(10)

在实际计算中,本文采用罚函数法[15-16]来解决约束优化问题.该问题为混合约束优化问题，可加入松弛变量[16],将不等式约束转化为等式约束,因此,式(9)可表示为

(11)

式中,sdp为第p个训练样本针对第d个不等式约束所施加的松弛变量.

采用PE类罚函数[16]将等式和不等式约束统一表示为

(12)

式中,Pl和Qd分别表示罚函数中等式和不等式约束的权值.

将罚函数添加到目标函数中，得到

(13)

上式可表示为

Ec=E+Ec1+Ec2

(14)

式中,E为常规误差,表征计算数据与样本数据的总体偏差;Ec1和Ec2分别为等式约束项误差和不等式约束项误差,表征计算数据满足等式和不等式约束条件的程度.其中，当模型计算结果满足不等式约束时,Ec2=0；否则,Ec2>0.

进而式(10)表示为

(15)

式中,I为m阶单位向量.

2.2 训练方法

根据上述对网络训练的描述,可采用BP算法进行训练,整理得到训练参数的调整量为

(16)

(17)

(18)

(19)

式中,Δsdp为松弛变量的调整量.

2.3 机理约束形式

在电厂实际运行过程中,系统机理约束一般表现为线性约束或者二次非线性约束.以等式约束为例，对线性约束和二次非线性约束的网络学习进行详细描述.

1) 线性约束,即

(20)

式中,hk为一次项系数；q为常数项.则有

(21)

(22)

(23)

2) 二次非线性约束,即

(24)

式中,hkk′为二次项系数.

(25)

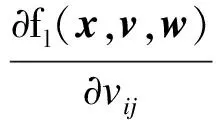
(26)

(27)

2.4 标准化方法

考虑到不同测点所对应的物理量及其变化幅度与取值范围可能有较大的差别,需要进行标准化处理,从而将原始测量数据映射到[-1,1]区间，即

(28)

(29)

3 基于H-RITNN的数据校正方法

基于H-RITNN的热工过程数据校正流程如图2所示,其流程如下：

① 对测量数据进行标准化处理;

② 建立系统平衡约束关系方程;

③ 建立新的网络训练目标函数;

④ 对H-RITNN网络进行训练,建立H-RITNN数据校正混合模型;

⑤ 采集实时测量数据,并进行标准化处理;

⑥ 通过H-RITNN网络模型计算得到实时数据的校正值;

⑦ 通过显著误差检测模块进行显著误差检测.

图2 基于H-RITNN的数据校正流程

4 算例分析

4.1 简单数学模型

考虑式(28)的五维非线性系统:

(30)

式中,γ为在区间[-1,1]中呈均匀分布的随机参数;ζ1～ζ5为服从N(0,0.002)分布的高斯白噪声.

由变量γ在区间[-1,1]内生成均匀分布的800组数据,取400组奇数组数据作为训练样本，分别建立非线性RITNN和H-RITNN模型,并在H-RITNN网络训练过程中加入下式线性等式约束:

f1(u)=u3-u2+0.15=0

(31)

f2(u)=u5-u4+0.25=0

(32)

选择剩余数据中的100组作为测试样本,并对u2和u4的第51组～第100组测试样本施加线性漂移误差fue,采用残差平方值(mean squared error,MSE)来考察模型精度，即

(33)

(34)

(35)

式中，N为测试样本序号.

图3给出了模型计算结果.由图可见，在同时存在多故障测点的情况下,本文模型仍能给出正确结果,并有效抑制显著误差的影响,减小残差污染.

图3 变量u2,u4的测试结果

采用绝对误差Eg来考察模型约束能力,模型测试结果如图4所示.由图可见，H-RITNN方法的计算结果在消除等式约束误差方面要优于RITNN方法,因此，H-RITNN网络估计值更加接近于真实值.

图4 2种等式约束测试结果比较

4.2 工程实例分析

以某1 000 MW机组热力系统1#高加为对象进行算例分析,选取表1所示的7个测点建模.分别在40%,60%,80%以及100%负荷稳定工况下采集数据,采样间隔时间为10 s,选用每分钟6次采样结果的平均值作为一组样本数据,共采集800组进行研究,其中600组数据采用IT-net,RITNN以及H-RITNN方法进行训练,其他数据用于模型测试,3种方法都采用1-5-7网络结构.

根据该机组的设计资料及实际运行数据可知，1#高加给水温升范围为18 ℃<ΔT<25 ℃,该温升不等式关系经标准化后得到

-0.056 3

(36)

将式(36)写成标准形式，得到等式约束1和等式约束2为

p=1,2,…,800

(37)

p=1,2,…,800

(38)

在训练样本中,对变量M5的第1组～第200组数据和M6的第200组～第500组数据分别添加20%的负向定值漂移误差和10%的正向定值漂移误差;在测试样本中,分别对变量M2,M5和M7添加如下的线性漂移偏差：

(39)

采用本文H-RITNN方法进行数据校正测试,并与IT-net和RITNN方法模拟结果进行比较.采用均方根误差(root mean squared error,RMSE)来考察模型精度，即

(40)

结果如表1所示.可见，当训练样本出现故障时,与IT-net方法相比,RITNN和H-RITNN方法能够更加准确估计各变量的真值,具有较强的故障检测能力.

表1 3种方法的均方根误差测试结果

进一步考察RITNN和H-RITNN模型结果是否满足原约束条件限制,其结果如表2所示.可见,采用RITNN方法的测点估计值大部分偏离约束，而采用本文H-RITNN方法计算结果则完全满足给定的约束条件,符合加热器的实际特性.

表2 2种方法的机理不等式约束测试结果

5 结语

本文提出了一种混合型鲁棒输入训练神经网络模型,将过程机理方程加入到RITNN网络的目标函数中,使得本文所提出的模型估计值能更好地满足系统内在机理性的规律.采用罚函数法对约束方程进行处理，并利用BP算法推导了H-RITNN网络各权值的调整公式,表明该网络的训练仍然类似于常规BP网络的训练方法,具有较高的学习效率.基于H-RITNN网络模型的非线性数据校正方法及流程,分别针对简单非线性系统和某1 000 MW机组1#高加系统进行了算例分析,结果表明H-RITNN方法能够较好地满足系统机理约束关系,可更加准确地给出数据重构结果.由此可见，本文模型对提高电厂热力系统在线监测精度和故障诊断的可靠性具有重要的实用价值.

)

[1]Soderstrom T A,Edgar T F,Russo L P,et al. Industrial application of a larger scale dynamic data reconciliation strategy [J].IndustrialandEngineeringChemistryResearch,2000,39(6):1683-1693.

[2]Wang X，Kruger U，Irwin G W．Process monitoring approach using fast moving window PCA[J].IntelligentSystemsandControlGroup，2005，44(15) ：5691-5702.

[3]Choi S W,Lee I B.Multiblock PLS-based localized process diagnosis[J].JournalofProcessControl,2005,15(3):295-306.

[4]司风琪,徐治皋.基于自联想神经网络的测量数据自校正检验方法[J].中国电机工程学报,2002,22(6):152-155.

Si Fengqi,Xu Zhigao.Self-verifying data validation method based on the autoassociative neural network(AANN)[J].ProceedingsoftheCSEE,2002,22(6):152-155.(in Chinese)

[5]Murty A K S. Material balance around a chemical reactor [J].ChemProcDes,1997,13(4):347-349.

[6]毕小龙,王洪跃,司风琪,等.基于核主元分析的传感器故障检测[J].动力工程,2007,27(4):555-559.

Bi Xiaolong,Wang Hongyue,Si Fengqi,et al.Detection of sensor faults by kernel principal component analysis[J].JournalofPowerEngineering,2007,27(4):555-559.(in Chinese)

[7]Antory D, Irwin G W,Kruger U, et al.Improved process monitoring using nonlinear component models[J].InternationalJournalofIntelligentSystems,2008,23(5):520-544.

[8]顾毅,顾坤发,李德恩,等. 数据校正与物料平衡软件在扬子石化芳烃厂的应用[J].数字石油和化工,2007(11):57-60.

Gu Yi,Gu Kunfa,Li Dean,et al.Data correction and material balance software at Yangzi petrochemical aromatics plant[J].DigitalPetroleumandChemical,2007(11):57-60. (in Chinese)

[9]王广军,何祖威,陈红.基于神经网络和过程机理的锅炉过热系统动态仿真[J].中国电机工程学报,2001,21(12):38-40,58.

Wang Guangjun,He Zhuwei,Chen Hong.Boiler evaluation system simulation based on neutral network and process mechanism characteristic[J].ProceedingsoftheCSEE,2001,21(12):38-40，58. (in Chinese)

[10]陈晓东,马广福,王子才.改进的Elman网络与机理模型的互补建模方式[J].系统仿真学报,1999,10(2):97-100.

Chen Xiaodong,Ma Guangfu,Wang Zicai. A mutually compensatory modeling method based on mechanism model and improved Elman network [J].JourneyofSystemSimulation,1999,10(2):97-100. (in Chinese)

[11]司风琪,李欢欢,徐治皋.基于鲁棒输入训练神经网络的非线性多传感器故障诊断方法及其应用[J].东南大学学报:自然科学版,2011,41(3):574-578.

Si Fengqi,Li Huanhuan,Xu Zhigao.A nonlinear multi-sensor fault diagnosis method and its application based on robust input-training neutral network[J].JournalofSoutheastUniversity:NaturalScienceEdition,2011,41(3):574-578.(in Chinese)

[12]司风琪,周建新,仇晓智,等.基于APCA的电站热力过程故障传感器自适应检测方法[J].东南大学学报:自然科学版,2009,39(2):282-286.

Si Fengqi,Zhou Jianxin,Qiu Xiaozhi,et al.Adaptive detection method of sensor failures based on APCA for the thermodynamic system in power plant[J].JournalofSoutheastUniversity:NaturalScienceEdition,2009,39(2):282-286.(in Chinese)

[13]Zhu Qunxiong,Li Chengfei.Dimensionality reduction with input training neural network and its application in chemical process modelling[J].ChineseJournalofChemicalEngineering,2006,14(5): 597-603.

[14]张正江,祝铃钰,邵之江,等.基于大规模严格机理模型的数据校正[J].高校化学工程学报,2008,22(5):877-882.

Zhang Zhengjiang,Zhu Lingyu,Shao Zhijiang,et al. Data reconciliation based on large scale rigorous model with equation oriented method [J].JournalofChemicalEngineeringofChineseUniversities,2008,22(5):877-882. (in Chinese)

[15]杜学武,张连生,尚有林,等.带有不等式约束的非线性规划问题的一个精确增广Lagrange函数[J].应用数学与力学,2005,26(12):1493-1499.

Du Xuewu,Zhang Liansheng,Shang Youlin,et al. Exact augmented Lagrangian function for nonlinear programming problems with inequality constraints[J].AppliedMathematicsandMechanics,2005,26(12):1493-1499.(in Chinese)

[16]韩艳丽.约束优化问题的罚函数的研究[D].焦作：河南理工大学数信学院,2011.