基于KPCA的FPSO流程故障检测方法

2013-12-20郝晓鹏赵洪业

电子科技 2013年5期

郝晓鹏，赵洪业，高强

(天津理工大学自动化学院，天津 300384)

主元分析方法(Principle Component Analysis，PCA)是在工业流程故障诊断中较为常用的一种数据驱动方法，它在数据趋于无穷大且基本满足线性关系的条件下，可以检测出故障［1－2］。但是，对于一个系统，含有故障的数据样本不可能趋于无穷大，即不可能让系统在故障状态下继续运行，并且由于系统本身或数据提取的问题，所获得的样本数据可能是非线性的。对于这样小样本、非线性问题，提出利用核主元分析方法(Kernel Principle Component Analysis，KPCA)进行解决，并利用浮式储油卸油生产系统(Floating Production Storage＆Offloading，FPSO)平台进行验证。

1 核函数

如图1所示，通过一个非线性映射函数φ(x)，将输入空间R映射到高维特征空间F，使得输入空间中的非线性或线性不可分问题在特征空间中能够进行线性分类［3－4］。其中，映射函数 φ(x)定义为

核函数定义为

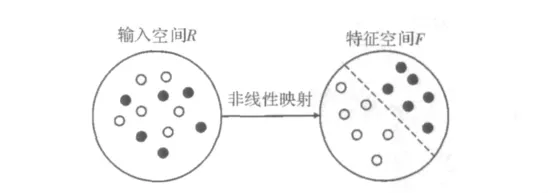
图1 非线性映射示意图

其中，φ(x)与φ(y)是输入空间的向量，x与y是在特征空间中的像。

如式(2)所示，输入空间的核函数实际是特征空间内积的等价。一般来讲，映射函数φ(x)比核函数K(x，y)复杂，即简单的核函数有时往往对着“复杂”的映射。因此，引入核函数能够大幅降低非线性变换的计算量。而核方法的优势就在于并不要求知道φ(x)的具体映射形式，而只要求已知核函数的具体形式。

目前，常用的核函数主要有3种，如表1所示。实际采用和研究最多的是高斯核函数。高斯核函数是局部性强的核函数，其外推能力随着参数σ的增大而减弱。本文的KPCA采用高斯核函数进行分析。

表1 常见核函数

2 KPCA方法

KPCA是一种非线性特征提取方法，该方法不直接计算数据的特征向量，而是首先利用一个非线性映射，将数据从低维的输入空间映射到一个高维的特征空间，然后在特征空间利用PCA方法进行线性主元分析。

2.1 KPCA算法

对于给定样本 xt:t=1，2，…，l，xt∈Rn，利用函数φ(·)映射到高维特征空间F(φ(xt))，计算其协方差矩阵［5－8］

式(3)所对应的特征方程为

求解式(4)的特征值λj≥0，以及特征向量Vj。

式(4)两边同时左乘φ(xt)得

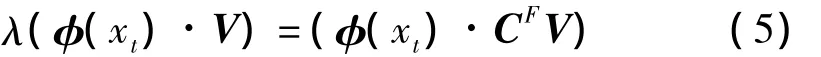
且对于λ≠的特征向量可表示为φ(x1)，φ(x2)，…，φ(xn)的线性张量，存在因子 αi，i=1，2，…，l使得

将(6)代入(5)得

定义 l×l矩阵 Kij=K(xj，xt)=(φ(xi)·φ(xj))代入式(7)得

其中，α =［α1，α2，…，αl］T，λk，λ1≥λ2≥…≥λl为特征值，其对应的特征向量为 Vk，k=1，2，…，l。

样本 xt在特征空间中的第 k，k=1，2，…，l个主元tk

其中，IN为1/N与一个N×N的单位矩阵相乘。

2.2 故障检测策略

基于KPCA的故障检测方法与PCA方法类似，在特征空间采用T2与SPE统计量来检测故障。T2统计量是主元向量的标准平方和，为

其中，ti由(7)式求得，Λ－1为主元的特征值构成对角阵的逆矩阵。

T2的控制限可通过F分布求得

其中，p为主元个数;N为样本数目。

SPE统计量是每次采样在变化趋势上与统计模型之间的误差，为

SPE统计的控制限为

其中，g与h是与SPE的均值与方差相关的常系数。

2.3 故障检测的步骤

(1)对数据进行预处理。(2)建立正常工况下的模型:1)将预处理后的正常数据进行标准化。2)计算核矩阵K，并利用式(10)对K进行均值中心化处理。3)在特征空间中计算正常数据的主元成分tk。4)计算正常数据的T2统计量与SPE统计量。5)确定T2与SPE的控制限。

(3)利用KPCA进行故障检测。1)对测试数据进行预处理与标准化处理。2)计算核矩阵K，并对K进行均值中心化处理。3)计算测试数据的T2统计量与SPE统计量。4)监视T2与SPE统计量，看是否超过正常数据的T2与SPE统计量，如果超过，表明有故障发生。

3 实验仿真研究

3.1 FPSO流程介绍

FPSO［9－10］典型生产流程中含有36个过程变量以及21个控制点，其中，调节型阀门9个，关断型阀门12个。本文从36个观测变量中选取18个过程变量用于过程监控，所有过程观测值均包含噪声。FPSO生产流程如图2所示。

图2 FPSO流程

在该典型流程中，设置8个故障，包括温度、压力变化引起的系统故障、传感器故障等。本文对故障1与故障5进行KPCA故障检测分析。

3.2 基于KPCA的FPSO流程故障检测仿真

在仿真实验中，核函数选用高斯核函数，σ取值为500，采用SPE统计量进行监控。故障1为一级分离器压力偏低所导致的系统故障，故障5为原油－水入口换热器原油出口温度传感器故障。图3(a)中，采用PCA方法不能有效地检测出故障，但从图3(b)所示，在180个点附近SPE值明显超过了SPE控制限，说明有故障发生。同理，图4(a)中，故障检测不明显，图4(b)中，在200个点附近明显检测出了故障发生。