一种敏感电路式露点测量方法

聂 晶 孟晓风 汪 烁 郑 睿

(北京航空航天大学惯性技术重点实验室，北京100191)

空气中水汽的含量，即所谓的湿度.湿度的精密、快速测量是化学传感器中的难点之一.通常用水汽压(也称绝对湿度)、相对湿度、露点温度、混合比，干湿球温度差和饱和比等物理量表示.其中露点温度的测量已被国际公认为最精密的湿度测量方法.

露点测量其关键技术在于露点的探测与识别.目前主要的露点识别技术有光电法、声波法以及图像识别法［1］.美国GE公司研制的光电精密露点仪、瑞士MBW公司生产的精密露点仪以及英国的MICHELL仪器公司生产的系列精密露点仪等均是基于露点冷凝面对光的散射效应来控制和生成露点.芬兰Vaisala公司推出的DM系列露点仪则是采用高灵敏度的声波代替光信号进行露点探测.文献［2－3］研究了新型显微成像式露点传感器，利用光学电容耦合器件对镜面生成露/霜前后图像的差异进行检测.

本文提出了一种利用考比兹电路特性对露点进行识别从而达到对露点温度测量的新方法，它能够在一些工作生产环境下提供一个快速的湿度预警.本方法具有测量方法简单、灵敏度高、可靠性好、成本低的优点.

1 实验系统

湿度敏感探头如图1所示，由一个谐振频率为6 MHz的AT切型石英晶体谐振器与一个半导体制冷器以及散热器组成.

图1 湿度敏感探头

将两面附有电极的AT切型石英晶体其中一面外围无电极区域与半导体制冷器的制冷面用导热银胶相贴，半导体制冷器的热面要与散热器相贴以便于发挥更好的制冷效果，从石英晶体的两个电极分别引出两根导线接入考比兹电路.同时需要两个PT100铂热电阻作为温度传感器，一个贴在石英晶体表面，用来提供石英晶体表面的温度值;另一个裸露在空气环境中，用来提供同一时刻下环境温度.

图2为实验系统框图，该系统数据采集卡采用PCI4712AS2高速采集卡，制冷器选取TEC1-3104型半导体制冷器，最大制冷功率为8.2 W，直流稳压电源可以同时为半导体制冷器提供0～3A的电流和为考比兹电路提供12 V电压，数字万用表采用FLUCK8508A八位半数字万用表，可以将PT100铂热电阻的电阻值直接转换为温度值，工控机为ADLINK工业控制计算机.

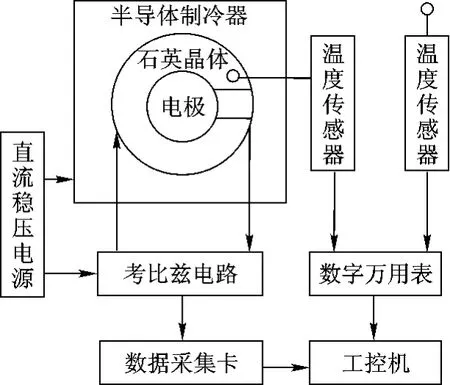
图2 实验系统框图

2 测量原理

考比兹电路是常规型的振荡电路，经常被用在石英晶体微天平［4－7］中作为驱动电路.作为敏感元件的石英晶体放在考比兹电路中只能被用在测量刚性吸附的质量变化，如果当石英晶体放在液相的环境下，其本身在电路中的特性发生改变导致电路无法满足维持振荡的条件而停止振荡，并且反应非常灵敏.本文就是利用考比兹电路的上述特性逆推出露点.

2.1 考比兹电路特性分析

在由晶体管构成的正反馈振荡的众多电路中，选取考比兹电路作为实验电路.图3是根据本实验选取的晶振所确定的电路，C1～C5为电容，R1，R2为电阻，Q1为三级管，VCC为电源，这些元件的具体参数根据晶体阻抗X的不同有所调整.

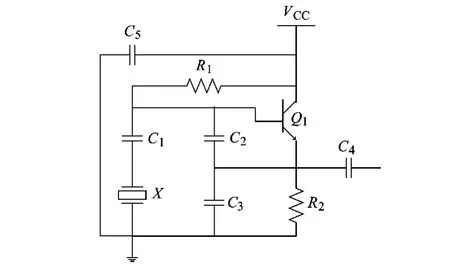
图3 考比兹电路

通过仿真可验证三极管工作在线性区内，满足工作要求.下面对电路的谐振条件进行分析.

图4为考比兹电路的等效电路.Ube=Ui，gm=β/Ri，β=β0/(1+jf/fβ)，其中 Ri为放大器输入电阻，β0为低频共射电流放大倍数;β为工作频率为f时晶体管电流放大倍数;fβ为晶体管共射截止频率.X1为晶振与 C1串联再与R1并联所得的阻抗，X2为C2的阻抗，X3为C3与R1并联所得的阻抗.

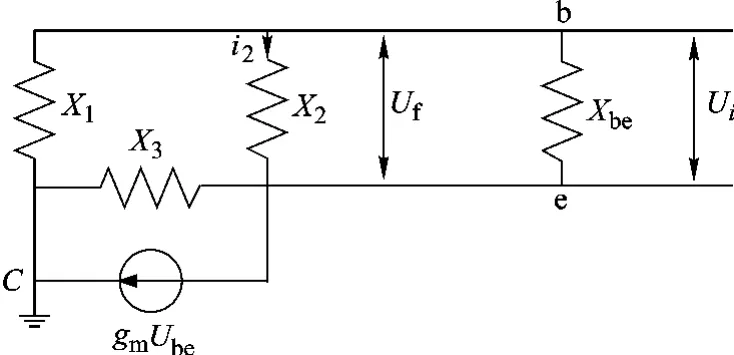
图4 考比兹等效电路

当电路处于谐振状态时，G=Uf/Ui应满足:

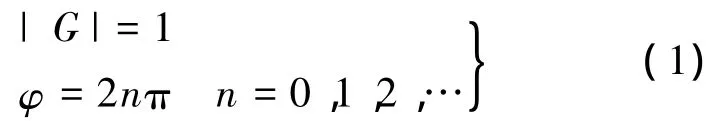
即幅度特性应满足总回路增益为1，频率特性应满足总回路相位和为 n×360°，n=0，1，2，….

当断开反馈，即将X2与三极管b极的连接点断开，从Uf向左看得

从电流源两端向上得

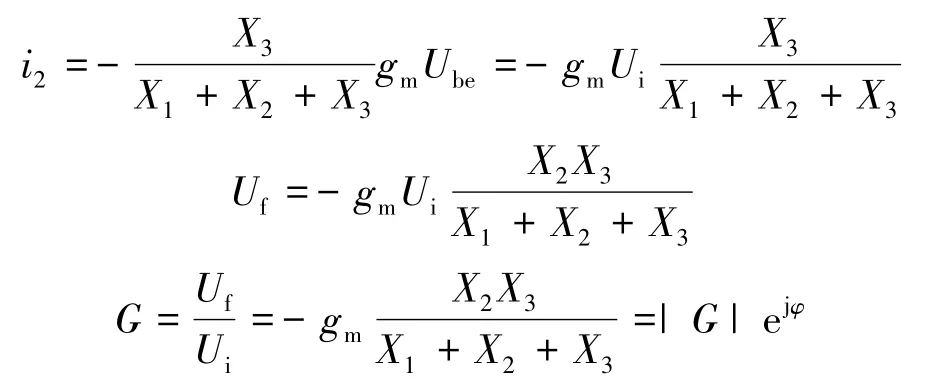
因为 G 满足|G|=1，φ=2nπ，n=0，1，2，…，所以有

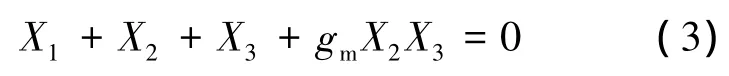
又因为 X2=1/jωC2，X3=R2/1+jωR2C3，所以有

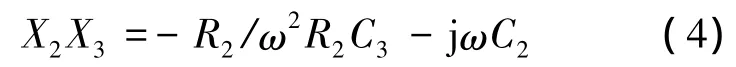
将式(4)代入式(3)得

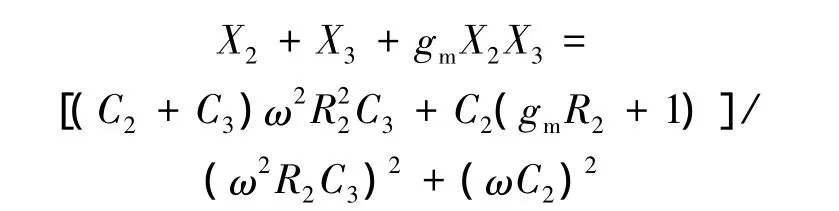
记为

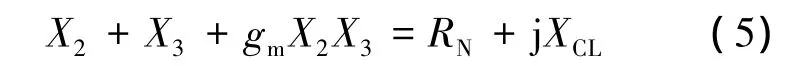
其中，RN为一个负gm电阻;XCL为外电路等效电容的阻抗.

为满足谐振条件，X1应等效为一个电阻与一个电感串联阻抗.

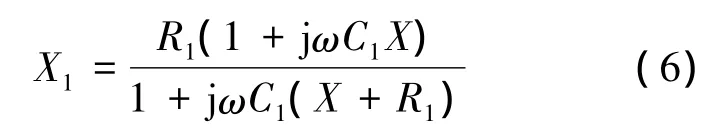
其中，晶体的阻抗X为

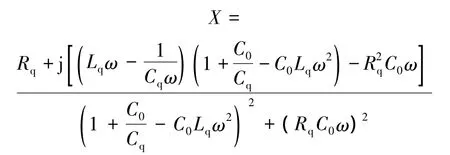
记为X=RX+jXIL，并将其代入式(6)得

记为

因为 Re+RN=0，Xe+XCL=0，XCL＜0，Xe＞0，所以

其中，Rq，Lq和Cq分别为动态电阻、电感和电容;C0为静态电容;ω为频率.

通过上述对考比兹电路的分析，可以得到考比兹电路维持振荡的条件.这种电路的特点是频率稳定性高，但是缺点是很难在液相环境下工作.

2.2 石英晶体电特性

石英晶体的等效电路如图5所示.Lq很大，一般为几十 mH到几十 H;Cq很小，一般为10－3pF量级;Rq很小，一般为几Ω到几百Ω;C0很小，一般约2～5 pF.

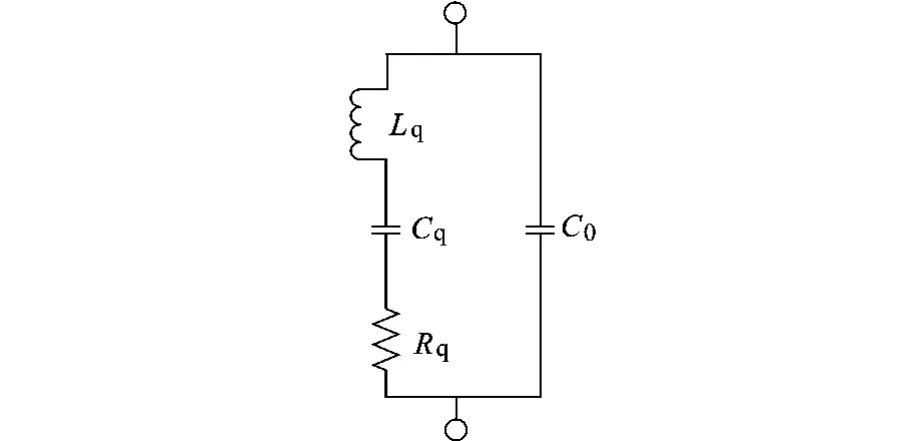
图5 石英晶体等效电路

为了分析此振荡电路在液体中很难工作的原因，给出石英晶体导纳的实部和虚部的关系曲线，如图6所示.

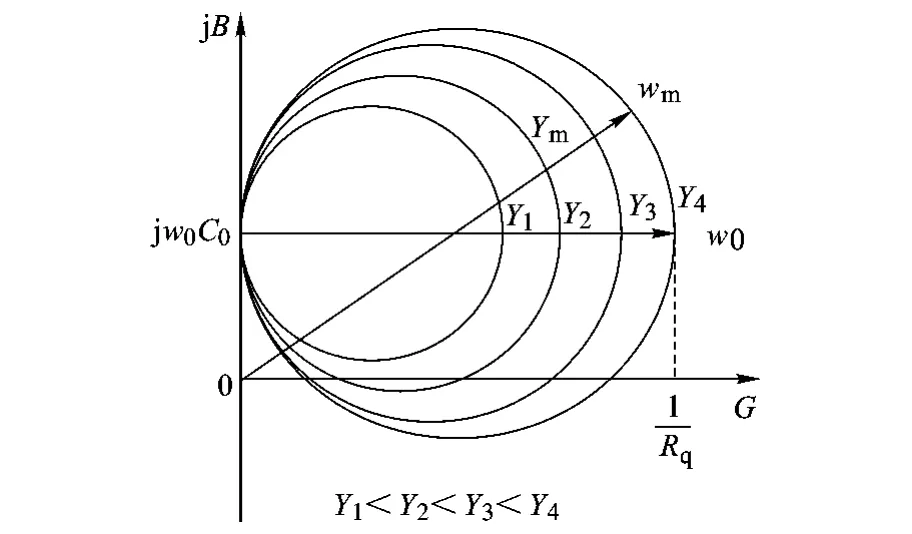
图6 石英晶体导纳的实部虚部关系曲线

随着Rq的增大，圆的半径不断减小;对同一个Rq，随着ω的增大，晶体导纳Y值在圆上逆时针移动.Y的表达式为

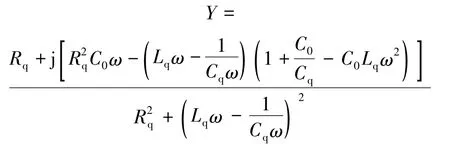
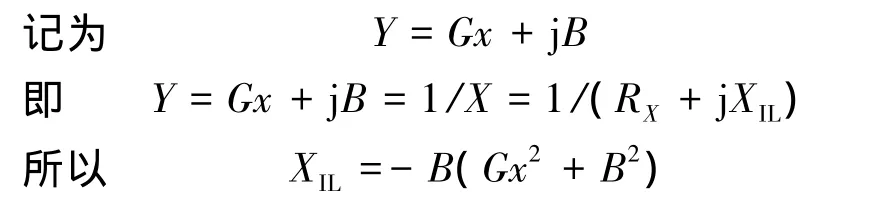
将XIL代入式(8)，若满足谐振条件，晶体必须呈感性.随着结露程度的加大，Rq逐渐增大到一定程度，使得XIL在晶体呈感性的频率ω处不能满足式(8)的条件，甚至晶体不能呈感性，此时电路一定不再满足谐振条件，停止振动.

3 露点测量

根据上面描述的晶体本身以及考比兹电路的特性，可以初步得知当制冷器开始对石英晶体制冷导致石英晶体表面开始结露的时候，由于在液体中晶体的等效电阻较大，放大器所提供的增益有限，幅度特性难以满足，并且在液体中引入的并联电容较大，使振荡电路的频率特性也难以满足，所以导致电路停止振荡，幅值和频率输出为零.依照图7所示的测量流程，选取了7组不同相对湿度环境对此测量方法进行验证.

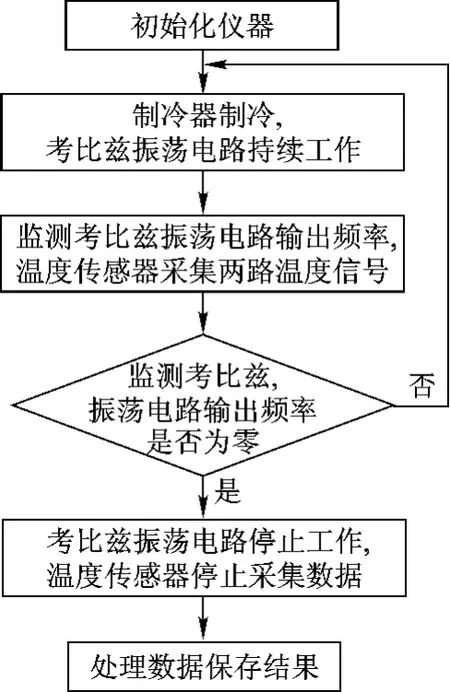
图7 测量流程

实验取2 V作为半导体制冷器的工作电压，环境温度为28℃.环境湿度根据HM1500电容式湿度传感器提供的数据为参考，精度为±3%.

图8为不同相对湿度下对应的理论露点温度和电路所对应的停止振荡时刻晶体表面温度的关系图.虚线数据是通过HM1500电容式湿度传感器提供的环境相对湿度与其对应的理论露点温度关系曲线，实线数据是已知相对湿度与测得的石英晶体表面温度的关系曲线.

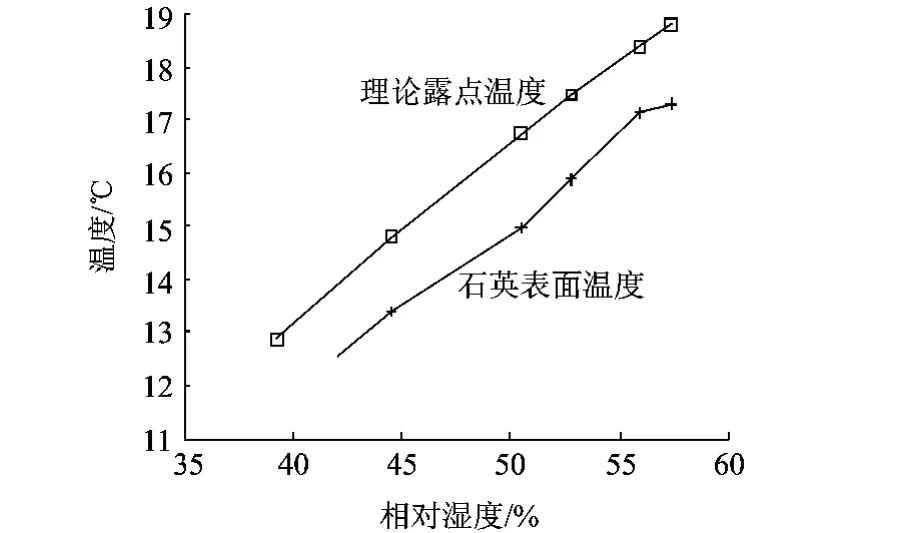
图8 实验结果

从图8以及根据前面描述的原理，可以看出对于考比兹电路的振荡条件与环境湿度存在着一定的对应关系，通过理论数据与实验数据对比分析，发现实验所测得的湿度趋势与提供的实际湿度趋势是相同的，并且露点温度的最大误差为1.59℃，所以在此方法中可以把电路停止振荡时刻晶片温度近似看作是环境的露点温度并能作为对空气湿度的高低做出快速判断的方法.

4 结论

1)根据实验系统的要求，设计出一套独立的露点传感装置，其具有灵敏度高、可靠性好、成本低的优点，并且可以适合较宽的湿度环境.

2)通过对晶体本身以及考比兹电路的特性分析，可以依据考比兹振荡电路的起振条件以及平衡振荡条件验证考比兹电路对不同湿度环境具有一定的敏感特性，并通过实验对比分析可以验证此方法可作为对空气湿度的高低做出快速判断的方法.

3)由于本文所采用电路的特性只与电路中石英晶体表面所处的湿度程度有关，排除了常规方法中温度及大气压力对测量结果的影响，并且导致电路停止振荡时刻的石英晶体表面结露程度是固定的，这决定了此方法具有很好的稳定性.

References)

［1］Rittersma Z M.Recent achievements in miniaturized humidity sensors—a review of transudation techniques［J］.Sensors and Actuators A，2002，96(2－3):196－210

［2］王进才，陈振林，张凤林，等.图像式露点测量仪器的功能开发［J］.分析测试技术与仪器，2000，6(3):158－161 Wang Jincai，Chen Zhenlin，Zhang Fenglin，et al.Image-sensitization condensation hygrometer［J］.Analysis and Testing Technology and Instrument，2000，6(3):158－161(in Chinese)

［3］Weremczuk J，Tarapata G，Paczesny D，et al.Fast dew point hygrometer with silicon integrated detector-Optimization of dynamic properties［J］.Sensors and Actuators A，2006，132(1):195 －198

［4］Sauerbrey G Z.Use of quartz crystal vibrator for weighting thin films on a microbalance［J］.Phys，1959，155:206－222

［5］Kanazawa K K，Gordon J G.The oscillation frequency of a quartz resonator in contact with liquid［J］.Analytica Chimica Acta，1985，175:99－105

［6］Hillman A R.The EQCM:electrogravimetry with a light touch［J］.Journal of Solid State Electrochemistry，2011，15(7－8):1647－1660

［7］Kwon S Y，Kim Y G，Yang I.Study on the melting and freezing behaviour of high temperature binary eutectic fixed points using differential scanning calorimetry［J］.Metrologia，2010，47(3):248－252