两种复合Cole-Cole模型的频谱差异研究与分析

徐汶东， 李敬兆， 于

(安徽理工大学 计算机科学与工程学院， 安徽 淮南 232001)

激发极化效应(Induced Polarization, IP)又称激电效应，是由岩、矿石及其所含水溶液在电流作用下所发生的复杂的电化学过程引起的[1]，但是到目前为止，人们对各种激发极化效应的成因和影响因素还没有统一认识，但已提出了多种模型来近似描述激发极化效应.在频域激电法中一般采用某一种极化模型进行正反演计算[2-3]，其中复Cole-Cole模型[4]是被广泛采用的一种，它有并联和串联两种形式.近几十年以来，尽管人们不断对激发极化效应的机理进行探讨[5-9]，但还没有新模型的出现.对于两种Cole-Cole模型的频谱特性，前人虽然已从多个方面进行了研究[10-15]，但还未从两种模型频谱对比的角度出发研究两种的差异，本文的研究力求填补这方面的空白.我们围绕复电阻率的幅值和相位这两个反演模型参数的指标，分析两种复Cole-Cole模型取相同参数和参数变化量相同时，两种模型复电阻率频谱差异，揭示在反演时，因两种模型选择上的不同而带来提取的参数不同的原因.本文的工作可以促进对激发极化机理的研究，为提出更准确的极化模型、提高激电法探测精度提供理论支持.

1 两种复Cole-Cole模型参数相同时的复电阻率频谱

复Cole-Cole模型[4]由Pelton等人于1978年提出，它由两个或两个以上基本模型组成，有串联和并联两种形式，其等效电路如图1所示.

图1 两种复Cole-Cole模型等效电路(左为串联,右为并联)

并联模型和串联模型的数学表达式见式(1)、(2).

(1)

(2)

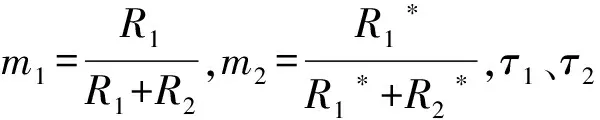
下面任意给定各参数相同时的初始模型，根据式(1)、(2)分别计算串联模型和并联模型的复电阻率，给出两种模型复电阻率幅值比ρratio和相位比φratio的曲线，如图2所示.

初始模型参数取值为：ρ0=10Ω·m,m1=0.4,m2=0.2,c1=0.3,c2=0.4,τ1=0.2,τ2=2.ρratioφratio按式(3)、(4)计算式中，abs表示取幅值，Ψ表示取相位，ρss表示串联模型的复电阻率，ρps表示并联模型的复电阻率.

(3)

(4)

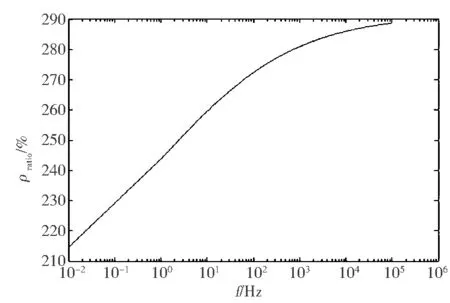
(a)幅值比

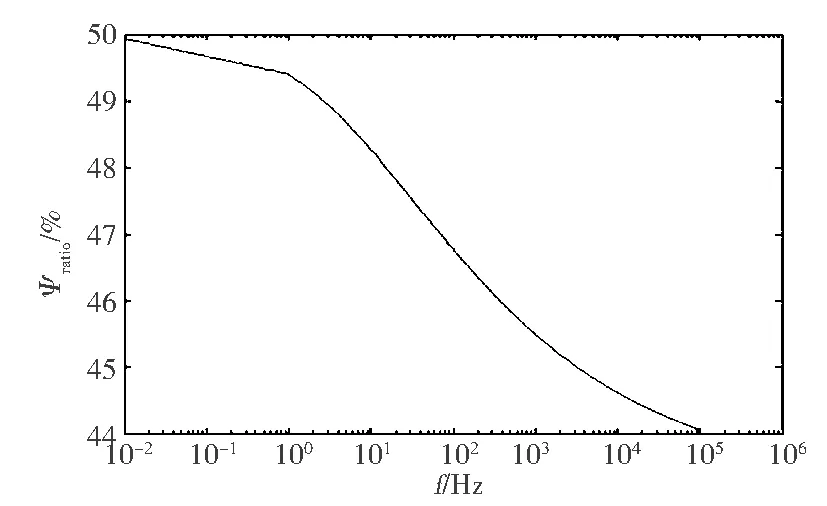
(b)相位比图2 串、并联两种复模型复电阻率比值

由图2中ρratio、φratio的数值可见,串联模型的复电阻率幅值是并联模型的两倍以上，而相位是并联模型的0.5倍以下，在中频段二者比值变化迅速，高频段渐缓；两种模型复电阻率幅值和相位差异非常明显，这说明两种模型表示的复电阻率极化效应是不一致的，如果用不同的复模型经过反演拟合来确定模型参数，反演结果必然存在差异.这种差异表明，对激发极化效应的机理还必须进一步研究.

2 两种模型在参数变化时的频谱差异

数据反演理论主要是根据参数的变化引起目标函数值的变化进行算法设计、参数提取[17-18].在工程实践中，参数变化带来实测数据变化,在激电法中主要利用复电阻率幅值和相位反演模型参数，推断地下介质的矿物组成.所以下面在两种模型同类参数变化量相同的情况下，从对复电阻率幅值和相位的影响程度大小的角度进一步分析两种模型的差异.

2.1 m参数变化时两种模型变化量的差异

并联和串联初始模型的参数选取与前面相同,令m1、m2参数同时变化±20%、其它参数不变时作为新模型，根据式(5)、式(6)计算复电阻率幅值和相位变化量的百分比率.

(5)

(6)

以上两式中, ρsx、ρpx表示某一个参数变化后的串、并联模型复电阻率,ρss、ρps、abs、Ψ的意义与前面相同.在m参数增加和减少时，两种模型复电阻率变化量百分比的对比曲线如图3所示.

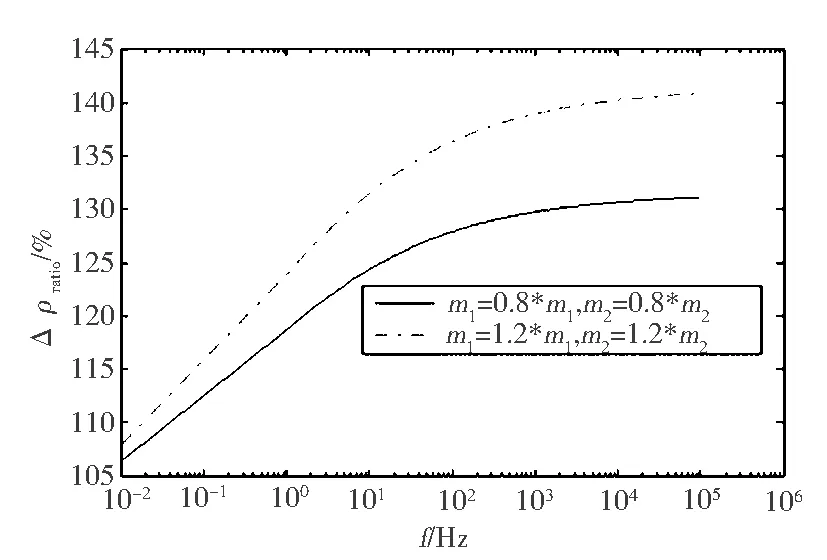
(a)幅值比

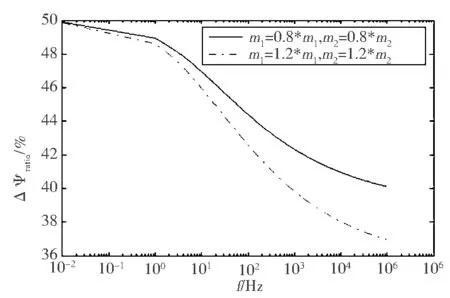
(b)相位比图3 m参数变化时串、并联两种模型复电阻率幅值和相位变化量之比

由图3可看出，串联模型的复电阻率幅值变化量大于并联模型的变化量，在较宽的频段上二者的百分比在110%以上，最高时达到140%；而串联模型的复电阻相位变化量小于并联模型的，二者的比值在50%以下，最低时达到30%.同时，m参数增大时，串、并联模型的复电阻率幅值变化量百分比大于参数减小时的变化量百分比；随着频率的增加,不论参数变大、变小，幅值变化的百分比都增加；而串、并联模型的复电阻率相位变化量百分比小于参数减小时的变化量百分比，且随着频率增加而减小，曲线在形态上与复电阻率变化量百分比曲线相反.总体来看，在m参数变化量相同时，两种模型幅值和相位变化量的差异是比较明显的，因此，在反演参数时，如果根据相同的变化量用不同的模型去反演，得到的m参数值也必然存在较大差异，这就造成了反演结果的差异.

2.2 c参数变化量相同时两种模型的差异

初始模型仍与前面相同,在其它参数不变的情况下,令c1、c2参数同时变化±20%时，按式(5)、式(6)计算的两种模型复电阻率变化量的对比曲线，如图4所示.

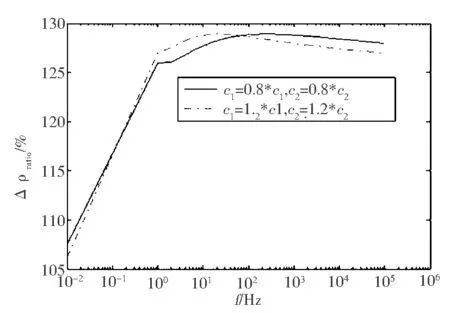
(a)幅值比

(b)相位比图4 c参数变化时串、并联两种模型复电阻率幅值和相位变化量百分比

由幅值百分比曲线可看出，在c参数增加或减少时，串、并联模型的复电阻率幅值变化量比值基本一致，只是在中、高频段的某些区域有所差异.串联模型复电阻率幅值变化量是并联模型的110%～130%，随着频率的增加，二者比值变缓并趋于定值；而从相位比值曲线看出，串联模型的相位变化量相对于并联模型的很小，只是在个别频点存在奇异值，二者相位变化量的差异十分明显.由于c参数的变化对两种模型复电阻率变化量影响的差异，选用二者之一的模型进行反演参数时,必然造成反演结果的差异.

2.3 τ参数变化量相同时两种模型的差异

还是选用前面的初始模型，现令τ1、τ2参数同时变化±20%时，按式(5)、式(6)计算两种模型复电阻率变化量的百分比曲线，如图5所示.

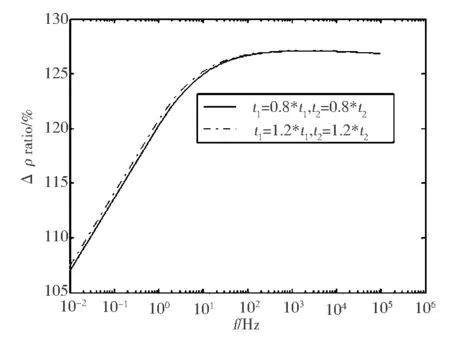
(a)幅值比

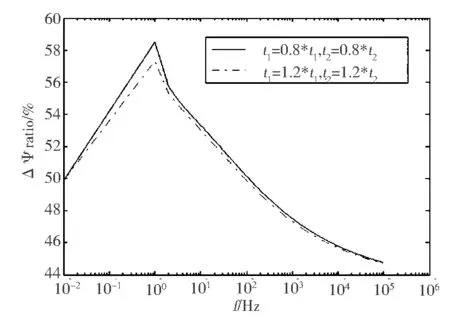
(b)相位比图5 参数变化时串、并联两种模型复电阻率幅值和相位变化量之比

由图5可见，不论τ参数增加或减少，两种模型的复电阻率幅值变化量的比值无论在高频段还是低频段基本一致，相位变化量的比值只是在很窄的低频段有所差异.串、并联模型复电阻率幅值变化量的比值，在中、低频段由1.08倍增加到1.25倍，在高频段比值趋于一个稳定数值；相位变化量的比值在中频段达到最大，然后随着频率的增加，比值渐小，曲线趋于平缓.不论参数τ增加或减少，两种模型复电阻率的变化量都存在差异，所以用不同的模型反演参数时也必然存在差异.

3 结束语

(1)在两种模型参数取值相同的情况下，串、并联模型复电阻率幅值和相位的差异在两倍以上，说明了两种复Cole-Cole模型描述极化效应的不一致性.

(2)当初始模型相同、同类参数变化量也相同时，两种模型复电阻率幅值的变化量都存在差异,复电阻率幅值的差异稍小、相位的差异尤其是c参数变化时相位的差异较大.并且随着频率的增加，二者的差异稳定在某一数值.这说明根据相同的数据，用两种复Cole-Cole模型反演参数时，其结果必然存在差异.

(3)从模型参数增加和减少时的百分比曲线对比来看,m参数变化时的比值曲线存在明显差异,且随着频率的升高,差异越明显；c、τ参数增加和减少时，在多数情况下比值曲线基本一致.这说明了m参数是影响模型复电阻率显著的参数.

本文的研究可以促进对激发极化机理的进一步探讨，以便尽早提出新型极化模型；同时也为提高激发极化法、复电阻率测井法的分辨力、以及去除瞬变电磁、CSAMT等方法中的激发极化效应提供理论支持.

[1]伯廷 J,洛布 J.激发极化法的实验和理论[M].北京：地质出版社,1980.

[2]柯马罗夫著 B A.激发极化法电法勘探[M].阎立光,译.北京:地质出版社,1983.

[3]Fu L K. Induced Polarizatlon Method[M]. Beijing:Geological Publishing House,1982.

[4]Pelton W H, Ward S H, Hallof P G,etal. Mineral discrimination and removal of inductive coupling with multifrequency IP [J]. Geophysics, 1978,43(3) : 588-609.

[5]Wait J R. Overvoltage research and geophysical applications[M]. London:Pergamen Press,1959.

[6]Fraser D C,Keevil Jr N B,Ward S H.Conductivity spectra of rocks from the Craigmont ore environment[J].Geophysics,1964,29(5):832-847.

[7]Madden T R, Cantwell T. Induced polarization: a review[J]. Mining Geophys，1967,2(part D):373-400.

[8]Dias C A. A non-grounded method for measuring electrical induced polarization and conductivity[D].Berkeley：Univ.California ,1968.

[9]Dias C A. Analytical model for a polarizable medium at radio and lower frequency[J]. Geophysics, 1972,77:4945-4956.

[10]Dias C A, Developments in a model to describe low-frequency electrical polarization of rocks[J]. Geophysics,2000,65:437-451.

[11]Pelton W H,Sill W R,Smith B D. Interpretation of complex resistivity and dielectric data,Part I[J].Geophysical transactions 1983,29(4):297-330.

[12]席振铢.层状极化介质频率域激发极化效应研究[D].长沙：中南大学，2002.

[13]尚晓,林品荣,李勇，等.层状极化介质激发极化效应研化究[J].物探化探计算技术, 2012(3):158-161.

[14]肖占山，徐世浙，罗延钟，等.岩石复电阻率频散特性的机理研究[J].浙江大学学报：理学版,2006,33(5)： 584-587.

[15]程辉,底青云,李帝铨.频率信号激励下岩石电性参数研究[J].地球物理学进展,2010，25(3):918-925.

[16]刘菘,关善友,高鹏飞.求极化椭球体真Cole-Cole参数的联合谱激电反演[J].地球物理学报,1994, 37(1):542-551.

[17]蔡军涛,阮百尧,罗润林.层状大地视真频参数测深曲线的反演[J].中南大学学报,2008，35(4):662-666.

[18]阮百尧.激发极化数据的最小二乘二维反演方法[J].地球科学,1999,24(6): 662-666.