家域研究进展

2013-12-16张晋东VanessaHULL欧阳志云

生态学报 2013年11期

张晋东，Vanessa HULL，欧阳志云

(1.中国科学院生态环境研究中心城市与区域生态国家重点实验室，北京 100085;2.绵阳师范学院，绵阳 621000;3.Center For Systems Integration and Sustainability，Department of Fisheries and Wildlife，Michigan State University，East Lansing，MI，48823，USA)

通常把动物特定的活动区域作为其家域［1］，家域的大小、形状、结构和位置受捕食者-猎物之间关系，种内、种间竞争［2-3］，领域行为、活动路线、隐蔽场所选择、优质及限制性资源分布模式［4-6］，以及种群密度、性别组成、社群压力和交配制度［4，7-9］等基础生态学过程的影响，因此家域的准确描述能为理解动物在特定时期生态学需求、取食策略、生境选择和行为规律等生态、行为学研究提供重要的视角［3，10-13］。本文结合国内外家域研究的最新进展，对动物家域的内涵，样本数据的获取方法与特征及其对估算结果的影响，家域估算模型及评价进行综述，总结家域研究的发展过程，并着重探讨3种代表性家域估算模型的优缺点，论述国内研究的优势与不足，提出未来研究展望，为动物家域的进一步研究提供参考。

1 家域的概念和内涵

家域的概念最早由Burt提出:动物个体进行取食、交配和育幼的正常活动区域［1］。这一概念未考虑时间因素，对“正态性”的应用含糊不清，被后来学者批评修正［10］，Kernohan提出相对综合性的家域概念:在一定的时间范围内，特定的动物出现概率(例如95%)的区域范围［10］。

关于家域内涵的理解，经历了只针对家域面积大小、形状，到强调动物在家域内对不同区域利用强度信息的过程［10］。1949年Hayne引入“活动中心”的概念，指出动物家域的生物学内涵应强调动物在活动范围内对不同部分的利用强度信息［14］。自20世纪80年代以来，利用分布的概念开始广泛应用于家域研究中，并为众多研究者所接受［15］。利用分布即通过对动物离散的活动位点模拟，量化动物在某特定时期出现在某区域的概率［10，16］，研究者选择概率水平或利用分布百分比定义动物的家域，通过利用分布的计算可预测动物可能出现的位置［16］。同时，“核域”取代“活动中心”成为家域研究中广泛应用的术语，家域中，利用强度高于随机分布的区域为核域［17］。多数情况下，家域内的食物，水等资源的分布是不均匀的，动物多选择资源丰富的地方生活，对于有核域的动物，其家域内的空间利用应是聚集分布而不是均匀或随机分布［3-4］。核域主要反映动物空间利用的生物学意义，不一定严格受家域大小的限制，有些动物的家域大小一致，但其核域可能不同，譬如，有些是家域中心位置取食者，有些是边缘漫游动物，即使它们的家域面积、形状一致，核域却不相同［4］。

2 位点数据的收集方法

动物活动位点为估算家域的基础，其收集方法直接影响家域估算的准确程度。目前，常见的收集方法包括:无线电遥测，可视化绘图，声波或超声波遥测，全球定位系统(GPS)项圈跟踪，直接观察法，红外线照相，以及分子粪便学等。其中，无线电遥测，即利用小型的、可重装的变动脉冲传感器来记录动物的活动位点，由于该技术能随时获取位点数据，装置轻便，自20世纪50年代以来，该技术就广泛应用于野生动物的行为监测研究中［18-19］。Laver和 Kelly总结了2004—2006年发表的141篇关于动物家域的文章，其中105篇利用无线电遥测获取位点数据［19］。然而无线电遥测有一定的局限性:误差较大，可能超过0.5km［20］;研究者必须距动物很近才能获得信号，会引起动物行为上的改变;跟踪需在白天和天气条件良好情况下进行，一般很难在夜晚进行;适用于生活在开阔生境的动物，对生活在复杂地形的动物并不适用［7］。很多研究并未注意到该技术存在的误差，Harris等总结了1984—1988年，发表在18个主要期刊上的93篇利用无线电遥测研究动物家域的文章，发现仅有不到三分之一的文章对无线电定位的精度进行了评价［7］。目前，动物野外跟踪技术的发展方向为GPS项圈，在获得4颗卫星信号的条件下，通过GPS项圈可以在95%的监测时间里，获得误差范围在20m之内的动物活动位点信息［21］，为研究者提供更多的连续活动位点、更长的监测时间和更远的监测距离，正越来越多的应用于动物家域估算，活动路径，活动模式等行为生态学的研究当中［13，22-24］。

3 样本含量和位点自相关对家域估算的影响

3.1 样本含量对家域估算的影响

样本含量是影响家域估算精确度的重要因素，估算的准确率会随着样本含量的增加而提高［15，25］，这就出现了最小样本含量问题，如利用正态理论模型估算家域，只有达到一定的样本含量，数据才能符合正态分布，理论上，最小的样本含量是当取样位点增加时家域估算的面积不再变大的临界样本大小［10］。面积-观察点曲线常被用来判断最小样本含量［19，26］，一些研究基于野外实验数据和计算机模拟(理想状态)数据，利用面积-观察点曲线确定最小样本含量(图1)。然而不同研究者的研究结果并不相同，甚至相互矛盾，例如，Gese通过最小凸多边形法，95%椭圆估算法和95%调和均值法计算郊狼(Canis latrans)家域的最小样本含量范围是23到36［26］，而Harris等的研究表明100—300个位点是满足最小凸多边形法最小样本含量要求［7］。Seaman等人提出利用核心密度估计法的最小样本含量应在50个以上［15］。面积—观察点曲线法只适用于判断一个恒定活动中心的动物的最小样本含量［27］，而很多动物有一个以上的活动中心，目前尚未有统一的标准或方法来确定最小样本含量［10］。家域估算的最小样本含量可能取决于研究动物的生物学特征［18］，位点数据的分布类型［15］，以及不同的家域估算方法［28］。因此，关于在具体分布类型和估算方法条件下判断家域估算最小样本含量的方法，需进一步探索与研究。

需要指出的是，尽管样本含量在家域估算中极为重要，但以往研究中并没有给予足够重视。Seaman等人总结了1980—1997年，发表在《Journal of Wildlife Management》上关于动物家域研究的101篇文章，其中，仅有49%给出了位点数目或范围信息，21%完全没有样本含量的信息，其余则只有相对模糊的样本含量信息，如只给出整个研究的总样本含量，或最小样本数，未详细给出每个研究动物的位点数目［15］。

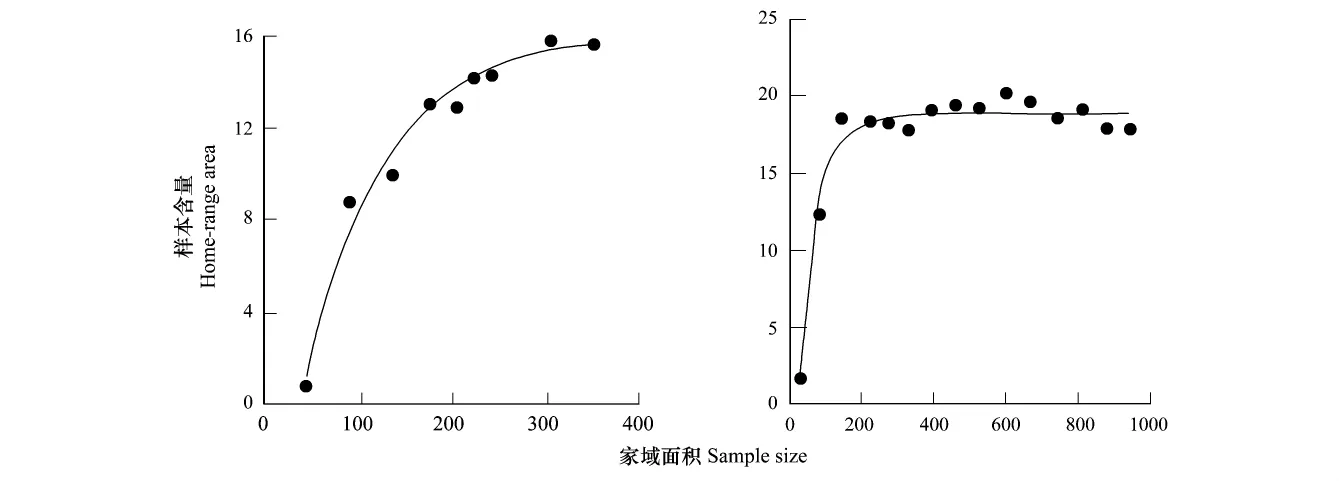
图1 利用面积-观察点判断家域估算中的最小样本含量［7］Fig.1 The minimum sample size needed to construct a home-range estimate，based on the asymptote of the Area-Observation Curve［7］

3.2 取样位点自相关对家域估算的影响

多数家域估算模型的前提假设是位点数据之间不存在自相关［7，29-30］，而事实上，位点数据之间的自相关普遍存在于动物家域的估算中［25，31］。多数学者认为位点数据自相关会导致家域估算结果误差增大，因为存在自相关的位点数据不能全部反映已确定的样本数量信息，即n个存在自相关的位点数据所反映的信息少于n个独立的位点数据［10］。为了解决位点数据自相关问题，Swihart和Slade提出运用比统计量检验，即利用位点间的距离与位点和中心点距离的比值来判断独立性位点数据间的时间间隔［30］，利用该方法的前提是研究动物只有一个活动中心，且研究期间的动物家域是静态的［10，25，30］。在掌握研究动物生物学习性的基础上，生物学意义上的独立性时间间隔(1d，2d或者1周)也可作为选取位点的时间间隔标准［18］。家域估算过程中，在总活动位点确定的前提下，增加取样数量、缩短取样间隔将会增加位点自相关程度;而延长取样时间间隔，将会导致样本含量减少，以上两者都会导致估算结果偏差增大，所以需在样本含量和取样密度之间进行权衡［18］。尽管有些研究针对样本含量和位点自相关导致的偏差提供了一些方法，然而无论在实际应用还是理论上这些方法所发挥的作用都是有限的，有必要发展更多的理论和方法来解决这些问题［18］。

也有一些学者对位点自相关是否重要持不同观点，譬如，Otis和White认为在动物家域估算中，足够的位点数目比位点间的独立性更重要［18］，Gese等人认为利用存在自相关与独立性的位点数据估算的家域结果没有明显差别［26］，还有研究表明:为满足位点数据之间的独立性而增加取样时间间隔将导致家域面积被低估［32］。Belant和Follmann认为家域估算中的动物活动位点本身不是独立存在的，而是先前运动位点和经验的一部分，所以根本不需要考虑位点自相关问题［33］。

总之，家域估算中的取样位点自相关是否重要，盲目给出任何结论都不适合，需综合考虑样本含量，取样位点的生物学、统计学意义以及估算模型类型等因素，再给出合适的处理。例如研究动物活动速度较快，那么取样位点自相关问题可不作为优先考虑的因素［7，32］。对于以概率为基础的估算模型，位点自相关对估算结果影响较大，而多边形为基础的估算模型受位点自相关的影响较小［7］。

4 家域估算方法的主要类型

家域的统计学含义为动物的运动轨迹被模拟成一个二维的，连续的，随机的而且具有位点自相关性质的函数过程［18，25，29］。自家域理论用于动物空间利用研究以来，发展出多种家域估算方法，可归纳为3个类型:多边形法，通过连接外围活动位点形成凸面或者凹面的多边形估算家域，如最小凸多边形法(MCP)，剥离多边形法，凹多边形法等［10］，其中 MCP 法为应用最早，目前最普遍的家域估算方法［1，15，19］;栅格单元法，通过计算动物活动位点在不同栅格中累积出现的数目，描绘出简单的三维活动范围等值线，如栅格单元计数法，由于此方法不能有效计算家域面积，加之概率法的出现，其应用相对较少［7］;概率法，通过假设某种特定的概率分布(如二维正态分布)模拟动物的利用分布，如傅里叶系列平滑法，调和平均值法，核心密度估计法(KDE)等［10］。由于概率模型能较好地区分动物对不同空间的利用强度，也能通过等值线方法确定家域大小和形状，成为目前最受研究者接受的方法，其中KDE法被一些学者认为是最适合的家域估算模型［10，19］。布朗桥运动模型(BBMM)考虑活动斑块间的路径方向和时间，是KDE法的延伸［13，34］。根据家域估算模型的应用程度及其发展过程与方向，本文重点介绍MCP法，KDE法和BBMM法。

4.1 最小凸多边形法(MCP)

最小凸多边形法是应用最多的估算动物家域的方法［19］，家域被确定为包含所有动物活动位点的凸多边形的最小区域:

式中，x和y是动物活动位点的向量坐标，n是样本含量［35］。MCP法完全依据外围位点生成家域，无需满足特定的统计分布类型［4］，由于计算简单，能直观地勾勒出研究动物整个的活动区域而被广泛应用［10］，1980—1997年，发表在《Journal of Wildlife Management》关于动物家域研究的101篇文章中，88篇利用MCP法，占 87%［15］。

然而该方法在很多方面受到质疑，首先，如图2所示，受异常值影响，个别边缘位点决定着家域面积大小，忽视了内部位点的信息，不能准确反应动物对不同空间资源的利用强度［4，10，19］。

图2 利用同一组数据不同方法模拟动物家域，其中(a)最小凸多边形法MCP，(b)核心密度估计法KDE(95%，h=234)Fig.2 Home ranges were estimated using(a)Minimum Convex Polygon and(b)95%Kernel Density Estimates using h=234

有研究表明，即使去掉外围的一些异常位点(如采取α零假设)，若不明确这些位点的生物学意义，也不能降低结果的偏差［35-36］;其次，一些研究表明MCP法对样本含量要求较高［7，15］;另外，以往MCP法分析家域，很少应用明确的渐近线分析，致使结果精确度模糊不清［19］。尽管MCP法饱受质疑，却仍是目前家域估算中应用最广泛的方法［10，15，19］，主要的原因是有学者认为 MCP 法是唯一可对不同研究进行比较的估算方法［7，37］，这一观点也受到一些学者的反对，他们指出由于MCP法存在上述诸多缺陷，继续采用将产生更多的不真实结果，不应继续用于动物家域的估算［19，38］。本文认为，如果只需了解动物活动的边界范围，MCP法仍为一种适合的选择［10］，若采取2种以上的方法估算家域，其中一种应为MCP法，或许是一种适宜的处理方式［7，37］。

4.2 核心密度估计法(KDE)

自Worton第一次应用KDE法估算动物家域以来［39］，KDE法成为最受欢迎的方法，Powell认为该方法代表着野生动物家域估算方法的发展方向［4］。

KDE基于位点数据，利用空间分布的非参数估计(如基于简单描述的估计，统计模型等)估算家域［10］，与多数家域估算方法类似，KDE法也假设位点数据是独立的，公式如下:

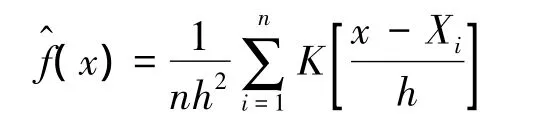
利用KDE法估算家域的最关键步骤是选择合适的平滑指数［16］，平滑指数也称h统计量，在动物家域研究中指估算家域的核心宽度，平滑指数决定了基函数围绕中心点的宽度，对家域模拟的结果存在特有的动态影响［41］，正确选择h对获得准确的估算结果至关重要，高估h值会产生更大且紧密的家域闭合曲线，致使估算结果偏大，h值过小则会产生过多的数据噪声，即很多小的、离散的家域闭合曲线(图3)。目前，判定h值的主要方法有3种，分别是最优平滑指数(href)法［16］，最小平方交叉验证法(LSCVh)和似然交叉验证法(Likelihood Cross-Validation，CVh)［28］。

图3 固定核心密度估算方法中，平滑指数对家域估算结果的影响Fig.3 The influence of smoothing parameter on the fixed kernel density home range estimator.Smoothing parameter(h)was selected using the LSCVh，CVh，href，and ad hoc(h=1000 m)methods

最优平滑指数href公式:

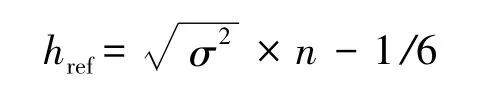
式中，σ2是样本横纵坐标的临界协方差，n是样本含量，在此指用于估算家域的位点数目［40］。href是以二维正态单峰分布为基础发展而来，对于二维正态分布型的拟合是适宜的［15］，然而href并不适合多维度数据的分析［16］。

最小平方交叉验证法，是在模型估计分布与真实分布的完全平方差(ISE)基础上推导而来［28］，最小完全平方差公式:

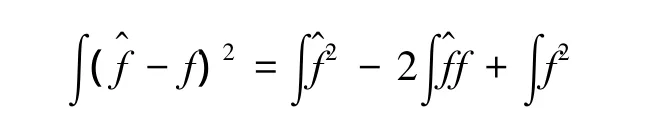
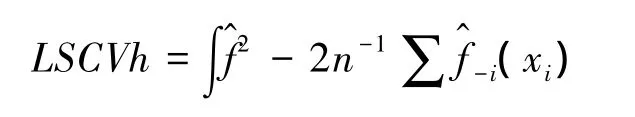
似然交叉验证法是建立在最小KL距离(The Kullabck-Leibler Distance)的基础之上的，而最小KL距离由信息理论发展而来，即通过KED法获得的利用分布概率与真实的分布f(x)之间的差异［28］，KL距离具体公式为:

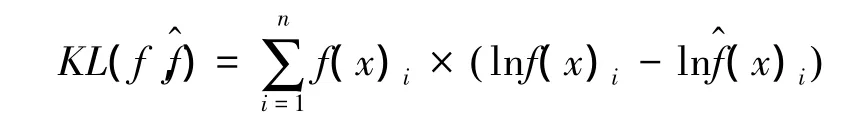
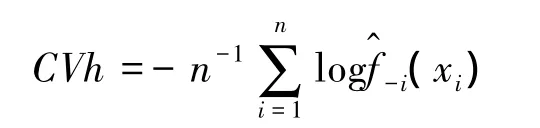
有研究比较了3种确定h值方法的优劣，Seaman等人的研究表明，与LSCVh相比较，利用href选择h值估算的家域偏差更大，表面积拟合度更低，href受样本含量的影响更大［15］。平方差的属性使LSCVh法对异常值过度敏感，导致对真实空间分布无典型意义(如存在自相关的某些位点等)的缺失值给予过高的权重，从而夸大了不典型位点在家域模拟过程中的作用，通过CVh计算得到的h值估算的家域结果与真实的利用分布更加接近，稳定性更高，尤其在样本含量小于50的时候［28］。利用KDE法估算动物家域时，平滑指数与样本含量相比较，后者对家域的结果影响更大，随着样本含量的增加，不同方法下平滑指数的选择对结果的影响开始变小，也就是说，平滑指数的选择针对小样本含量的家域估算意义更大［15，28］。

4.3 布朗桥运动模型(BBMM)

家域研究中，模拟一定时间段内［0，Ttotal］动物在二维空间上的利用分布，可获得n个按时间顺序活动轨迹上的离散观测点，在不能明确动物活动模式的情况下，可将动物运动假设为随机运动或与之相对应的连续布朗运动［44］。利用沿着一定运动轨迹的n个离散的随机观测点可以估算动物对某一区域的利用频率，并且可以模拟每对连续活动位点的期望运动路径，扩展布朗运动到每对起始和结束位点，相对应的随机过程称为布朗桥［13］。BBMM函数是在核心密度估计函数的基础上发展形成的，如图4所示，模型由1个布朗桥概率密度函数将2个二维正态概率密度函数相连接，该方法既考虑了每个活动中心，也考虑了动物的活动路径，有效地避免了将活动斑块之间没被利用的区域误作为动物的家域［13，34］。

BBMM中有2个参数，参数1控制连接2个活动位点间“桥”的宽度，参数2控制活动斑块的宽度，功能上与传统核心密度估计方法的平滑指数h值类似［13，34］。Bullard第一次将布朗桥引入到动物家域估算中［34］，继而Calenge引入软件程序执行对动物家域的估算［46］。在此基础之上，Horen和Garton提出了包括有误差位点数据的模型推导和利用最大似然估计估算布朗运动方差的方法，具体公式如下［13］:

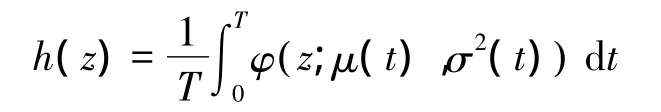
式中，σ2(t)=Tα(1-α)σ2m+(1- α)2δa2+ α2δb2，α =t/T。h(z)即为动物在 t时刻(t∈ [0，T])，经过 a，b两点间的概率密度函数，其中σm2被称为布朗运动方差，是与动物迁移速度相关联的扩散系数，可以通过观测位点的最大似然估计估算。δ2是遥测技术产生的误差(如由GPS项圈自身产生的误差)，可通过独立的实验计算［13，34］。

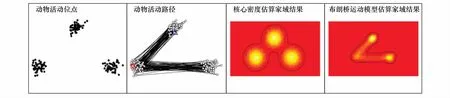
图4 核心密度估算方法与布朗桥运动模型的比较［45］Fig.4 Example comparison of kernel and Brownian bridge home range estimation methods;Depicted are locations of an example animal，movement paths of the animal，the fixed kernel density estimate and Brownian bridge movement model estimate of the animal's home range［45］

由于基础假设的不同，与其他模型相比，BBMM法处理位点自相关和不均等时间间隔问题的方式更为合理，在确定位点数据不是独立性的前提下，有效地将时间因素整合到模型当中［13，34］。另外，BBMM模型中的参数具有生态学意义，考虑到了动物移动速度和测量位点误差，而传统核心密度估算法的参数只是某种概率分布下的统计参数，未涉及到生态学过程［4，34］。BBMM法在运算过程中对数据要求较高，GPS项圈技术能够长期、连续，更大距离地获得动物位点数据，满足BBMM法的应用，而其他技术如通过无线电遥测等获得的数据很难达到 BBMM 法的分析要求［13，34］。

5 家域估算模型评价

对于描述动物的空间利用和影响动物活动的生态学过程，选择一个合适的家域估算模型至关重要，这就需要建立评价最适估算模型的客观标准［47］。传统的家域模型评价是通过综合多个标准对已有模型进行整体的概括描述，评价其适合度，进而总结每个模型的优缺点，如Kernohan基于最小样本含量，位点自相关敏感性，是否基于利用分布理论，参数还是非参数估计，能否估算多个活动中心，对异常值的处理能力，是否可以进行不同研究间比较等7个标准综合评价了12个模型的优劣［10］。此外，还有利用计算机模拟理想状态的家域，假定为真实的“家域”，然后根据每种估算模型的结果对其前提假设和方法的适合度进行检验［15-16］，然而，针对特定的数据，该方法不能得出连续性的、清楚的和广泛意义上的标准来确定最适模型［47］，而且该方法主要建立在二项式均匀分布和二项式正态分布基础之上，由于零假设很难与生物学意义联系在一起而遭到质疑［48］。Horen和Garton将信息理论引入到家域模型的评价中，该方法有3方面优点:(1)降低了评价家域模型的要求，传统方法必须知道动物的家域，该方法利用动物的活动数据即可执行模型评价;(2)最适模型将从一系列恰当权衡适合度与复杂性的模型中选出;(3)在未来的研究中，将有更多的生态学因子被整合到家域模型中，模型复杂性将增加，而信息理论更适用于评价复杂的模型［47］。

6 结语

通过家域的研究，能够描绘出一幅关于研究动物一系列重要基础生态学信息的示意图，在动物生态理论研究和保护管理应用中都具有重要意义［4］。家域估算模型作为家域研究中最核心的内容经历了3个发展阶段:第1阶段，旨在确定家域的大小和形状，如MCP法，由于受异常值的影响，不能区分动物在家域内对不同区域的利用强度，而倍受批评［19］。第2阶段，将概率论、非参数统计方法结合到家域研究中，如KDE法，尽管在如何客观获得平滑指数(h)的问题上也存在争议，却仍得到了多数研究者的认可，并广泛应用于家域估算中［10，19］。KDE法受到的最大批评是没有考虑时间因素和生态学过程［13，49］，第3阶段，估算模型考虑了动物的运动过程和时间，如BBMM法。

改革开放以来，动物家域研究在国内也得到很大关注，相继有学者研究了大熊猫(Ailuropoda melanoleuca)、小熊猫(Ailurus fulgens)、黑冠长臂猿(Nomascus concolor jingdongensis)、川金丝猴(Rhinopithecus roxellanae)、羚牛(Budorcas taxicolor bedfordi)、藏狐(Vulpes ferrilata)、马麝(Moschus sifanicus)、原麝(Moschus moschiferus)、斑羚(Naemorhedus goral)、黑叶猴(Trachypithecus francoisi)、野猪(Sus scrofa ussuricua)、狼(Canis lupus)及海豚(Sousa chinensis)等哺乳动物的家域［6，50-60］，此外，针对鸟类和两栖、爬行类动物也开展了一些相关工作［9，61-63］。国内研究更注重从动物自身的生物学特征与需求角度出发，分析动物个体的年龄、性别、体重和食性等生物学特性与其家域行为的关系［9，50，52，64-65］;探讨食物资源丰盛度、生境特征与质量、季节变化等环境因子对家域模式的影响［3，6，51-53，56］。研究者将家域与栖息地的选择与利用，食性，行为模式等研究有机结合起来，能更深入地揭示动物对家域内资源的空间利用方式和适应性行为策略的机制。然而，与国外的研究相比，国内研究主要是针对不同物种，应用现有的模型进行家域估算，在家域概念本质内涵、模型创建方面缺乏探索，而且很少考虑样本含量、位点自相关等因素对估算结果的影响。更多的研究尚处于第1阶段，主要关注于家域的大小和形状，近几年，才有一些研究开始应用 KDE法进行家域估算［37，51，61，63，66］。在今后的研究中，应尝试在案例研究的基础上，建立更适合的估算模型，如将研究动物的生态学特征结合到家域模型的创建之中，探讨家域的理论内涵，同时也应采取适当措施处理样本含量和位点自相关等问题，以提高家域估算结果的准确度。

自从家域作为正式的概念以来，家域的研究得到众多研究人员的关注，出现了一个高密度的研究发表时期［19］，随着对家域内涵的理解逐渐深入，家域模型估算方法也不断更新，然而，家域研究中仍存在着一些问题，诸如如何确定最小样本含量，位点数据自相关问题的处理，不同估算方法间不具备比较性等，今后有必要围绕下述方面开展重点研究:

(1)探索能统一、整合、评价不同家域研究方法的标准，提高家域研究结果的可比性。过去研究中的很多理论、方法和结果并不一致，甚至相互矛盾［19］，需要我们继续探索统一的理论方法进行家域研究，允许各个研究之间能进行直接的比较。

(2)加强家域研究与其他生态学模型的结合，发展既描述家域，同时包含其他生态学研究的多重模型。BBMM法将运动与家域模型结合起来，能更准确地研究家域，也能阐述动物的运动过程［13］;通过核心密度函数与生境选择模型的结合，能更准确地量化动物的生境选择偏好［11］。今后的研究应尝试与生态位模型、活动节律等更多的生态学研究相结合，获得更接近真实情况的家域模型。

(3)构建机理家域模型，构建在考虑资源、社会关系等生物学因素影响下动物家域模型。动物在景观尺度上的分布并不是单一的，景观结构函数，社会等级关系，利用斑块资源含量等因素也强烈地影响着动物的空间分布特征［5］。目前，多数的家域研究是基于活动位点，很少考虑动物自身生物系特性以及环境资源的数量和质量，有必要将景观结构，资源可得性，不同个体之间的竞争等生物学过程［5］，温度、光照等环境因子融入到家域模型中［67］，能够更好地理解动物家域特征形成的原因。

(4)加强理论研究与管理应用的结合，加深科研人员和管理者对影响动物空间利用的环境因子的理解。管理者在利用家域的研究结果时，应对研究方法和结果进行总结，需注意到不同方法和理论计算结果的差异，以做出更为科学、合理的决策［19］。

［1］ Burt W H.Territoriality and home range concepts as applied to mammals.Journal of mammalogy，1943，24(3):346-352.

［2］ Stamps J A，Krishnan V V.Territory acquisition in lizards:Ⅲ.Competing for space.Animal Behaviour，1995，49(3):679-693.

［3］ Liu Qz X，Wang X M，Wang Z H.Comparison on the biological characteristics of different functional partitions of the home range of Tibetan fox.Acta The riologica Sinica，2009，29(4):432-438.

［4］ Powell R A.Animal Home Ranges and Territories and Home Range Estimators//Luiqi B，Todd K F，eds.Research Techniques in Animal Ecology:controversies and consequences.New York:Columbia University Press，2000:65-110.

［5］ Mitchell M S，Powell R A.A mechanistic home range model for optimal use of spatially distributed resources.Ecological modelling，2004，177(1/2):209-232.

［6］ Huang Z H，Zhou Q H，Huang C M，Meng Y J，Wei H.Home range and daily ranging distance of Francois'langur(Trachypithecus francoisi)in Nonggang Nature Reserve，Guangxi，China.Acta Teriologica Sinica，2011，31(1):46-54.

［7］ Harris S，Cresswell W J，Forder P G，Trewhella W J，Woolard T，Wray S.Home-range analysis using radio-tracking data-a review of problems and techniques particularly as applied to the study of mammals.Mammal Review，1990，20:97-123.

［8］ Stamps J A，Krishnan V V.Territory acquisition in lizards.IV.Obtaining high status and exclusive home ranges.Animal Behaviour，1998，55(2):461-472.

［9］ Wang S G，Zeng Z Y，Wu P F，Lan Z J，Wang Y Z.The home range of Phrynocephalus vlangalii.Journal of Sichuan University(Natural Science Edition)，2004，41(2):403-408.

［10］ Kernohan B J，Gitzen R A，Millspaugh J J.Analysis of animal space use and movements//Milspaugh J J，Marzluff J M，eds.Radio tracking and animal populations.Academic，New York，USA，2001:125-166.

［11］ Marzluff J M，Millspaugh J J，Hurvitz P，Handcock M S.Relating resources to a probabilistic measure of space use:forest fragments and Steller's jays.Ecology，2004，85(5):1411-1427.

［12］ Mcgrath P E.Site fidelity，home range，and daily movements of white perch，Morone Americana，and striped bass，Morone Saxatilis，in two small tributaries of the York river，Virginia［D］.The college of William and Mary，2005:16-20.

［13］ Horen J S，Garton E O，Koren S M，Lewis J S.Analyzing animal movements using Brownian Bridges.Ecology，2007，88(9):2354-2363.

［14］ Hayne D W.Calculation of size of home range.Journal of mammalogy，1949，30(1):1-18.

［15］ Seaman D E，Millspaugh J J，Kernohan B J，Brundige G F，Raedeke K J，and Gitzen R A.Effects of sample size on kernel home range estimates.Journal of Wildlife Management，1999，63:739–747.

［16］ Worton B J.Using Monte Carlo simulation to evaluate kernel-based home range estimators.The journal of wildlife management，1995，59(4):794-800.

［17］ Samuel M，Green R.A revised test procedure for identifying core areas within the home range.Journal of Animal Ecology，1988，57(3):1067-1068.

［18］ Otis D L，White G C.Autocorrelation of location estimates and the analysis of radio tracking data.The journal of wildlife management，1999，63(3):1039-1044.

［19］ Laver P N，Kelly M J.A critical review of home range studies.The journal of wildlife management，2008，72(1):290-298.

［20］ Rodgers A R，Rempel R S，Abraham K F.A GPS-based telemetry system.Wildlife Society Bulletin，1996，24:559-566.

［21］ Wells D E.Guide to GPS positioning.Fredericton，New Brunswick，Canada，Canadian GPS associates，1986.

［22］ Ren B P，Li M，Long Y C，Grüter C C，Wei FW.Measuring daily ranging distances of Rhinopithecus bieti via a global positioning system collar at Jinsichang，China:a methodological consideration.International Journal of Primatology，2008，29:783-794.

［23］ Yamazaki K，Kozakai C，Kasai S，Goto Y，Koike S，Furubayashi K.A preliminary evaluation of activity-sensing GPS collars for estimating daily activity patterns of Japanese black bears.Ursus，2008，19:154-161.

［24］ Zhang J D，Hull V，Huang J Y，Zhou S Q，Li R G，Liu D，Huang Y，Li D S，Xu W H，Zhang H M，Liu J G，Ouyang Z Y.Circadian activity pattern of giant pandas during the bamboo growing season.Acta Ecologica Sinica，2011，31(10):2655-2661.

［25］ Swihart R K，Slade N A.On testing for independence of animal movements.Journal of Agricultural，Biological，and Environmental Statistics，1997，2(1):48-63.

［26］ Gese E M，Andersen D E，Rongstad O J.Determining home-range size of resident coyotes from point and sequential locations.The journal of wildlife management，1990，54(3):501-506.

［27］ Gautestad A O，Mysterud I.The home range ghost.Oikos，1995，74(2):195-204.

［28］ Horne J S，Garton E O.Likelihood cross-validation versus least squares cross-validation for choosing the smoothing parameter in kernel home-range analysis.Journal of Wildlife Management，2006，70(3):641-648.

［29］ Dunn J E，Gipson P S.Analysis of radio telemetry data in studies of home range.Biometrics，1977，33:85-101.

［30］ Swihart R K，Slade N A.Influence of sampling interval on estimates of home-range size.The journal of wildlife management，1985，49(4):1019-1025.

［31］ Powell R A.Black bear home range overlap in North Carolina and the concept of home range applied to black bears.Bears:Their Biology and Management，1987，7:235-242.

［32］ Reynolds T D，Laundré J W.Time intervals for estimating pronghorn and coyote home ranges and daily movements.The journal of wildlife management，1990，54(2):316-322.

［33］ Belant J L，Follmann E H.Sampling considerations for American black and brown bear home range and habitat use.Ursus，2002，13:299-315.

［34］ Bullard，F.Estimating the home range of an animal:a Brownian bridge approach［D］.University of North Carolina，Chapel Hill，North Carolina，USA.1999.

［35］ White G C，Garrott R A.Analysis of wildlife radio-tracking data.San Diego:Academic press San Diego，1990.

［36］ Burgman M A，Fox JC.Bias in species range estimates from minimum convex polygons:implications for conservation and options for improved planning.Animal Conservation，2003，6(1):19-28.

［37］ Liu X Q，Wang X M，Wang Z H，Liu QX，Ma B.Comparison of the Tibetan fox(Vulpes ferrilata)home range size using methods the fixed kernel estimation and the minimum convex polygon.Acta Theriologica Sinica，2010，3(2):163-170.

［38］ Böerger L，Franconi N，Michele G，Gantz A，Meschi F，Manica A，Lovari S，Coulson T.Effects of sampling regime on the mean and variance of home range size estimates.Journal of Animal Ecology，2006，75(6):1393-1405.

［39］ Worton B J.Kernel methods for estimating the utilization distribution in home-range studies.Ecology，1989，70(1):164-168.

［40］ Silverman B W.Density estimation for statistics and data analysis.London:London Chapman and Hall，1986.

［41］ Hemson G，Johnson P，South A，Ruthripley R K，Macdonald D.Are kernels the mustard?Data from global positioning system(GPS)collars suggests problems for kernel home-range analyses with least-squares cross-validation.Journal of Animal Ecology，2005，74(3):455-463.

［42］ Sain S R，Baggerly K A，Scott D W.Cross-validation of multivariate densities.Journal of the American Statistical Association，1994，89(427):807-817.

［43］ Jones M C，Marron J S，Sheather S J.A brief survey of bandwidth selection for density estimation.Journal of the American Statistical Association，1996，91:401-407.

［44］ Turchin，P.Quantitative analysis of movement.Sunderland MA:Sinauer Associates，1998.

［45］ Calenge C.Home Range Estimation in R:the adehabitatHR Package.Office national de la classe te de la faune sauvage Saint Benoist-78610 Auffargis-France，2011.

［46］ Calenge C.The package“adehabitat”for the R software:a tool for the analysis of space and habitat use by animals.Ecological Modelling，2006，197:516-519.

［47］ Horne J S，Garton E O.Selecting the best home range model:an information-theoretic approach.Ecology，2006，87(5):1146-1152.

［48］ Anderson D R，Burnham K P，Thompson W L.Null hypothiesis testing:problems，prevalence，and an alternative.Journal of Wildlife Management，2000，64:912-923.

［49］ Kie J G，Matthiopoulos J，Fieberg J，Powell R A，Cagnacci F，Mitchell M S，Gaillard J M，Morrcroft P R.The home-range concept:are traditional estimators still relevant with modern telemetry technology.Philosophical Transactions of the Royal Society B:Biological Sciences，2010，365:2221-2231.

［50］ Hu J C，Schaller G B，Johnson K G.The feeding ecology of giant pandas in Tangjiahe Natural Reserve.Journal Sichuan Teach College，1990，11(1):1-13.

［51］ Zhang Z J，Hu J C，Yang J D，Li M，Wei F W.Food habits and space-use of red pandas Ailurus fulgens in the Fengtongzhai Nature Reserve，China:food effects and behavioural responses.Acta theriologica，2009，54(3):225-234.

［52］ Fan P F，Jiang X L.Effects of food and topography on ranging behavior of black crested gibbon(Nomascus concolor jingdongensis)in Wuliang Mountain，Yunnan，China.American journal of primatology，2008，70:871-878.

［53］ Li B G，Chen C，Ji W H，Ren B P.Seasonal Home Range Changes of the Sichuan Snub-Nosed Monkey(Rhinopithecus roxellana)in the Qinling Mountains of China.Folia Primatologica，2000，71:375-386.

［54］ Song Y L，Zeng Z G，Zhang J，Wang X J，Gong H S，Wang K W.Home range of golden takin(Budorcas taxicolor bedfordi)in foping Nature Reserve，Shanxi，China.Acta Theriologica Sinica，2000，20(4):241-249.

［55］ Liu Q X，Richard B H，Wang X M，Wang Z H.Home range size and overlap of Tibetan foxes(Vulpes ferrilata)in Dulan County，Qinhai Province.Acta Theriologica Sinica，2007，27(4):370-375.

［56］ Yang Q S，Feng Z J，Wang Z W，Liu W L，Li X C，Silang O Z.Home range of the alpine musk deer(Moschus sifanicus)in the southeast area of Tibet autonomous region.Acta Theriologica Sinica，1998，18(2):87-94.

［57］ Wu J P，Zhang Y，Fu D F，Lan W X.Comparison of home range of Siberian musk deer and goral in winter.Journal of northeast forestery university，2008，36(1):58-60.

［58］ Wang W，Zhang J，Ma J Z，Liu H B.Analysis on wild boars home ranges in south Lesser Khingan Mountains.Acta Theriologica Sinica，2007，27(3):257-262.

［59］ Yang H J，Zhang H H，Dou H S，Shen X Q，Yan W B，Zhang Y，Gui M Q，Bao M R，Chen J R M T.Home range and habitat utilization of wolves during winter in Hulunbeir，inner Mogolia，Journal of northeast forestry university，2006，34(4):52-53.

［60］ Hung S K，Jefferson T A.Ranging patterns of Indo-Pacific humpback dolphins(Sousa chinensis)in the Pearl River estuary，People's Republic of China.Aquatic Mammals，2004，30(1):159-174.

［61］ Xu J L，Zhang X H，Sun Q H，Zheng G M，Wang Y，Zhang Z W.Home range，daily movements and site fidelity of male Reeves's pheasants Syrmaticus reevesii in the Dabie Mountains，central China.Wildlife Biology，2009，15:338-344.

［62］ Zhao S Y，Huang J W，Meng L，Tian Y，Tang S X，Hu H J.Comparison of home range between different color morphs of Lanius schach in winter.Sichuan Journal of Zoology，2010，29(4):543-546.

［63］ Qi Y，Zachary F，Dai Q，Wang Y，Yang Y，Wang B，Wang Y Z.Post-breeding movements，home range，and microhabitat use of plateau brown frogs Rana kukunoris in Zoige Alpine Wetland.Acta Zoologica Sinica，2007，53(6):974-981.

［64］ Li Y K，Leng LP，Gan Y Y，Zhang C X.Review of researches on home ranges of primates.Chinese Journal of Wildlife，2010，31(6):338-341.

［65］ Song C J，Yang X Z，Li Y，Qin L，Gao J.Effects of season，sex and age on the home range of giant panda in Qinling mountains.Chinese wildlife，2006，27(3):21-24.

［66］ Liu Q X，Wang Z H，Wang X M.A comparison of two home range core estimators for Tibetan fox(Vulpes ferrilata).Acta Theriologica Sinica，2009，29(1):26-31.

［67］ Quan RC，Ren GP，Behm J E，Wang L，Huang Y，Long Y C，Zhu J G.Why Does Rhinopithecus bieti Prefer the Highest Elevation Range in Winter?A Test of the Sunshine Hypothesis.PloS one，2011，6(9):e24449.

参考文献:

［3］刘群秀，王小明，王正寰.藏狐家域功能分区及其生物学特性比较.兽类学报，2009，29(4):432-438.

［6］黄中豪，周岐海，黄乘明，蒙渊君，韦华.广西弄岗黑叶猴的家域和日漫游距离.兽类学报，2011，31(1):46-54.

［9］王硕果，曾宗永，吴鹏飞，蓝振江，王跃招.青海砂蜥的巢域研究.四川大学学报(自然科学版)，2004，41(2):403-408.

［24］张晋东，黄金燕，周世强，李仁贵，刘巅，黄炎，李德生，徐卫华，张和民，刘建国，欧阳志云.大熊猫取食竹笋期间的昼夜活动节律和强度.生态学报，2011，31(10):2655-2661.

［37］刘晓庆，王小明，王正寰，刘群秀，马波.固定核空间法和最小凸多边形法估计藏狐家域的比较.兽类学报，2010，30(2):163-170.

［50］胡锦矗，Schaller G G，Johnson K.唐家河自然保护区大熊猫的觅食生态研究.四川师范学院学报(自然科学版)，1990，11(1):1-13.

［54］宋延龄，曾治高，张坚，王学杰，巩会生，王宽武.秦岭羚牛的家域研究.兽类学报，2000，20(4):241-249.

［55］刘群秀，王小明，王正寰.青海省都兰县藏狐家域范围及重叠度.兽类学报，2007，27(4):370-375.

［56］杨奇森，冯祚建，王祖望，刘务林，李新春，斯朗欧珠.西藏东南部地区马麝家域的研究.兽类学报，1998，18(2):87-94.

［57］吴建平，张勇，付东风，兰文旭.原麝与斑羚冬季家域的对比.东北林业大学学报，2008，36(1):58-60.

［58］王文，张静，马建章，刘海波.小兴安岭南坡野猪家域分析.兽类学报，2007，27(3):257-262.