差分CLEAN算法在编码板成像中的应用*
2013-12-16贾振卿霍卓玺周建锋
贾振卿,霍卓玺,周建锋
(1. 清华大学工程物理系天体物理中心,北京 100084;2. 粒子技术与辐射成像教育部重点实验室(清华大学),北京 100084;3. 高能辐射成像国防重点学科实验室,北京 100084)
由于硬X及γ射线照射物质时绝大部分会穿透或发生作用,很难像可见光一样发生反射和折射,因此对于较高能量的硬X射线和γ射线难以采用传统的光学聚焦方式成像,通常采取调制型成像技术[1]。该技术用硬件方法实现X射线源在时间或空间上的调制,而后用软件方法解调得到图像信息。
编码板成像是一种常用的硬X射线调制成像方法,属于对观测信号进行空间调制的类型。编码板成像由小孔成像推广发展而来,最初用于实践的编码成像设备就是在平板上分布有大量随机生成的小孔。但由于该设备无法同时满足提高角分辨率和灵敏度的需求,后来被经过专门设计的编码板取代。如NRA(Non-Redundant Arrays)编码板在理论上已经拥有了近乎完美的参数[2],但由于成像质量受噪声因素严重制约,转而被用作医学成像以及光学和红外波段的天体成像。NRA推广得到的URA(Uniformly Redundant Arrays)编码板[3]已经得到了成功应用,但仍有只能配合特定尺寸探测器使用的缺陷。此外还有PNP(Pseudo-Noise Product)[4]、Geometric-Mask[5]等其他设计类型的编码板。
编码板成像的具体过程是先经由编码板对射线源进行空间调制,观测结果称为阴影图(shadowgram)。阴影图是被观测物体图像与编码板矩阵的卷积结果。为了获取被观测物体的图像,需要对阴影图进行反卷积重建[6]。观测图像的重建过程通常是根据阴影图和编码板解码矩阵之间的相关运算得出的。这一过程可以由交叉相关算法或各种反卷积类型的图像重建算法实现[7]。对于理想的编码板成像系统,其PSF(Point Spread Function, 即点扩展函数,此处为编码板矩阵和解矩阵的相关结果)是δ函数。此时交叉相关方法可以获得很好的重建结果。在实际的系统中,由于要考虑半编码区域和探测器间隔、探测器死像素等因素,点扩展函数不再是δ函数,在主峰之外还带有旁瓣,因此交叉相关重建的图像中往往存在一些很强的鬼像。此外,由于观测天区往往存在着比较强的本底,使得弱源不仅会受到强源的干扰,还会淹没在背景噪声中难以分辨。对于这些缺陷,交叉相关法都没有很好的解决办法。因此,为了满足高质量成像的需求,需要采取更好的重建算法。
CLEAN算法是常用的反卷积图像重建算法之一。它是由荷兰科学家Högbom(1974)提出的一种成像算法[8],它最初被应用到干涉阵的成像处理中。干涉阵与编码板成像系统相似,采样的数据往往比较稀疏,经过傅里叶变换后的图像重建结果存在很强的旁瓣效应,和真实的图像相去甚远,只能算是“脏图”。CLEAN算法是从脏图出发,用一组δ函数逼近源真实的图像,通过迭代运算消除脏图中的旁瓣,最终获得与真实的图像很接近的“净图”。后来Schwarz 于1978年经过深入的数学理论分析和探讨[9],证明CLEAN算法不仅仅是一种消卷积算法,而且是一个滤波过程,具有很高的信噪比。使用CLEAN算法能够有效消除鬼像和本底噪声。
后来发现CLEAN过程存在着一些不合理之处[10-12]。实际观测中数据通常采取不等间隔采样,后处理时还需要对数据进行网格化、插值等操作。另外探测器中普遍存在损坏的单元。传统CLEAN的处理方法是基于一些模型估计这些单元的数据,这些操作都会在脏图中引入额外的噪声。传统的CLEAN过程直接从“脏图”出发,不能在后续的迭代中避免这些额外噪声的影响。另外CLEAN算法无法有效抑制强的本底,不利于弱源的探测。
1 差分CLEAN算法
差分CLEAN算法针对传统CLEAN的上述缺陷进行了改进。该算法从“脏图”中估计出部分真实信号(即模型信号)后,不是直接在脏图上进行CLEAN操作,而是求出模型信号在所有探测器上对应的模型观测数据,把实际观测数据与模型观测数据的差值当作下一次CLEAN的起始点。采用差分CLEAN算法可以消除数据缺失、不等间隔采样以及后处理过程中引入的人为噪声,得到更好的图像质量。
对于编码板成像系统,差分CLEAN算法的具体实现过程如图1。
首先通过交叉相关算法由阴影图获得脏图,并在其中寻找亮度最高的点P。假设被观测区域的图像由一系列点源组成。由于阴影图是被观测物体图像与编码板矩阵的卷积,因此可以认为P点位置必然有来自真实点源的贡献。这一贡献的比例可以根据经验加以估计,在CLEAN中通常用一比例系数g表示。将P点的亮度乘以g,得到对应位置的模型分量,并加入模型图中。模型图与编码板矩阵卷积得到的模型阴影图就可以作为被观测点源在阴影图中部分真实贡献的估计。
然后从阴影图中去除这部分贡献,再以残余的阴影图作为差分CLEAN下一次迭代的起点,重复上述步骤,直到残余图中没有明显的结构,则终止迭代。CLEAN算法可以保证收敛[13],通常选取残图中最亮点的强度小于3倍标准差作为终止迭代的条件。至此可以认为已经在CLEAN过程中将阴影图所包含的真实图像信息移除并保存到模型图中。
要还原这些图像信息只需要将模型图与理想的点扩展函数卷积,加上迭代终止时最终的残余图,就可以获得CLEAN的结果净图。

图1 编码板成像的差分CLEAN算法流程示意图
Fig.1 Flowchart of the Differential-CLEAN algorithm
2 数值模拟
为验证程序算法的可行性,首先分别采用交叉相关算法、传统CLEAN算法以及差分CLEAN算法对模拟数据进行了成像过程的检验。
在编码板图像重建过程中,通常用一个矩阵M表示编码板。M矩阵中元素1对应码板上镂空的探测单元,0代表遮挡的部分。探测结果D可以表示为被探测天区S与M的卷积,再加上背景B。通常编码板在设计时会采用特殊优化的方案,可以比较简单地求出M对应的反卷积矩阵G,使得M与G的卷积(即该码版的点扩展函数)为δ函数。同时由于本底为一可测量的常量,能够消除,从而可以由探测结果D重建观测的天体图像:
S′=DG=(SM+B)G
(1)
在模拟过程中首先生成编码板矩阵M。由于后续工作中将对INTEGRAL卫星上IBIS望远镜的ISGRI探测器数据进行处理,所以这里生成的矩阵与该探测器实际使用的MURA编码板矩阵相同[14],包括4个中心对称的单元,每个单元由相应阶数的Jacobi数组生成(参见图2)。同时反卷积所用的矩阵G可以很容易地由M矩阵得到:
G=2M-1
(2)
M与G卷积得到的即是编码板的点扩展函数,比较接近理想的δ函数,这也保证了MURA编码板拥有良好的成像效果。
模拟使用的原始图像由4个较为分散的点源组成。每个点源在图像空间占9个像素,图像空间内每个像素投影到探测器上恰好对应一个单元。单个像素流强分别为120 mCrab、110 mCrab、30 mCrab、10 mCrab,并加入了随机泊松噪声,噪声在探测器单个像素上引起的响应平均水平为最弱源最强响应处的100%。同时随机将10%像素单元的值设为0,用来模拟探测器损坏造成的数据缺失。由给定的原始图像与理想的编码板矩阵生成观测图像,采用3种算法分别对这一观测结果进行重建。其中CLEAN算法中的强度比例系数g(即每次迭代从最亮点P处提取的模型流强与残余流强的比值为g)取0.01。模拟结果分别如图3、图4、图5,其中最弱的一个点源强度与噪声相当,若事先并不知道其存在则很难分辨。

图2 INTEGRAL卫星上IBIS望远镜所采用的MURA编码板
Fig.2 MURA mask of IBIS on the INEGRAL satellite

图3 模拟数据的交叉相关算法结果(即脏图),该图的均方差为4.0 mCrab,其他详细数据见表1
Fig.3 Results of the cross-correlation algorithm applied to sim- ulated data. The root-mean-square deviation of the map is 4.0mCrab. Other details of the data are shown in Table 1

图4 模拟数据的CLEAN结果,其残图的均方差为2.9 mCrab,其他详细数据见表1
Fig.4 Results of the CLEAN algorithm applied to the simulated data. The root-mean-square deviation of the residual map is 2.9mCrab. Other details of the data are shown in Table 1

图5 模拟数据的差分CLEAN结果,其残图的均方差为2.7 mCrab,其他详细数据见表1
Fig.5 Results of the Differential-CLEAN algorithm applied to the simulated data. The root-mean-square deviation of the residual map is 2.7mCrab. Other details of the data are shown in Table 1
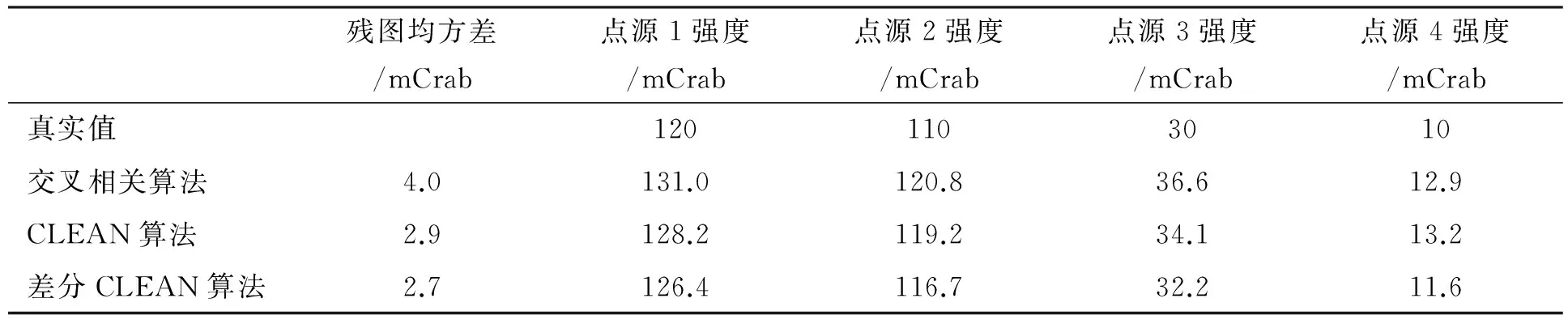
表1三种算法对模拟数据的重建结果
Table1Reconstructionresultsofthesimulateddatawiththreealgorithms
残图均方差/mCrab点源1强度/mCrab点源2强度/mCrab点源3强度/mCrab点源4强度/mCrab真实值1201103010交叉相关算法4.0131.0120.836.612.9CLEAN算法2.9128.2119.234.113.2差分CLEAN算法2.7126.4116.732.211.6
交叉相关算法对编码板的图像重建结果中,在4个点源周围可以看到十分明显的鬼像。这是由于编码板的点扩展函数并非真正的理想δ函数,而是存在着旁瓣。这些旁瓣会在反卷积的过程中产生鬼像。采用传统CLEAN算法和差分CLEAN算法处理模拟数据的结果可以看出鬼像都得到了较好的抑制,已经基本观测不到鬼像的存在。对理想点源的重建效果二者没有显著区别。加入10%的坏像素后,差分CLEAN的重建结果拥有更低的噪声水平,重建出的点源强度也更为接近真实值。若取30%的像素点为坏像素,差分CLEAN结果的残图均方差为2.7,CLEAN结果的残图均方差为3.0。与维纳滤波、Lucy迭代等算法相比,差分CLEAN算法不会引入伪结构,能够给出确定的迭代终止条件,并且对噪声不敏感,在原始数据部分缺失的情况下仍能得到较为理想的重建结果[15]。
3 INTEGRAL IBIS数据处理
INTEGRAL宇宙观测卫星[16-17]由欧洲航天局(European Space Agency, ESA)于2002年10月17号成功发射。INTEGRAL卫星由2 500个硬X射线探测单元组成,探测器总面积2 500 cm2。设计的成像角分辨率为15′。INTEGRAL载有两台主要的伽玛射线观测设备SPI和IBIS。前者主要用于能谱测量,后者用于成像。两台设备各自拥有能量分辨和角分辨本领,但是进行了不同的优化,使得两者能够形成互补,获得更好的整体效果。另外还有两台监测设备JEM-X和OMC分别提供X波段和光学波段观测上的补充。SPI、IBIS、JEM-X都是编码板成像设备。
IBIS编码板成像系统包括了一个MURA编码板,以及两组与编码板大小基本相当的伽马射线探测器。其中ISGRI是低能段探测器(15 keV~1 MeV),PICsIT是高能段探测器(175 keV~10 MeV)。
IBIS的完全编码视野(FCFOV)为8°×8°,理论角分辨率12′。ISGRI每个像素的大小为5′, PICsIT每个像素的大小为10′。IBIS的MURA编码板尺寸为11.2 mm×11.2 mm×16 mm,ISGRI探测器为128×128的CdTe晶体阵列,每个单元的尺寸为4 mm×4 mm×2 mm,单元中心间的距离为4.6 mm。PICsIT为64×64的CsI探测器,单元尺寸是8.4 mm×8.4 mm×30 mm,单元间距9.2 mm。
这里处理的数据是由ISGRI探测器采集,观测数据保存在FITS文件中,与处理模拟数据的流程不同,在处理实际数据时还需针对仪器的实际性能进行相关的修正。
首先探测器采集单元与编码板单元的尺寸并不一致,因此不能将实际观测数据简单地代入之前的模拟程序,而是需要根据探测单元与M矩阵的比例先对数据进行插值。程序中采取了比较成熟的双线性插值,根据探测器和编码板的尺寸可以计算得出插值需要的各项参数。
其次,因为探测器的视野有限,被探测区域在探测器各单元上探测到的强度是不同的,还需要对图像进行强度修正。具体实现的方法为逐点除以某个修正矩阵,修正矩阵由强度完全均匀分布的探测结果进行反卷积得到。需要注意的是修正矩阵的边缘存在十分接近0的元素, 这样修正后图像的边缘区域的涨落很大,信噪比很低。因此在实际数据处理中,一般把这些图像区域剔除。
图6、图7、图8为使用交叉相关、CLEAN以及差分CLEAN对ISGRI探测器实际数据(如图6,目标为Crab源)的处理结果,图中坐标单位均为像素,亮度为取自然对数后的结果。可以看到交叉相关算法的处理结果中有着较为明显的旁瓣结构存在;CLEAN算法的结果中旁瓣已经得到了较好的抑制,但背景强度较高,此外还可以看到一些亮度明显低于周围的像素点,这是由于探测器的损坏单元导致的;差分CLEAN算法同样取得了良好的重建效果,消除了鬼像,背景噪声的绝对强度和残图的涨落均低于其他两种算法的结果。

图6 OSA预处理后得到的阴影图。观测的开始、结束时间分别为2004-09-04T20∶15∶52至20∶18∶03。选取的能道为15~20 keV,包含130×134个像素单元
Fig.6 The shadowgram pretreated by the OSA. The observation lasted from 2004-09-04T20∶15∶5 to 20∶18∶03. There are 130×134 pixels included in the selected channel of 15KeV to 20KeV
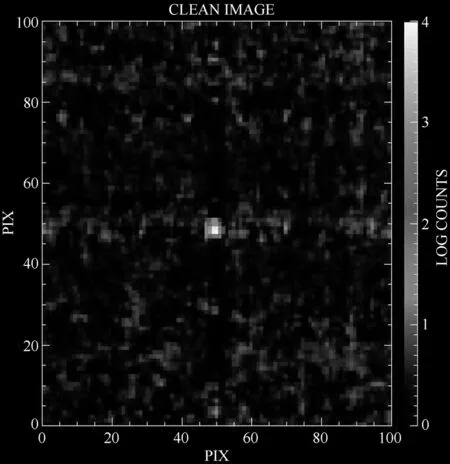
图7 图6所示数据的交叉相关重建结果,其均方差为424 counts/s
Fig.7 Results of the cross-correlation algorithm applied to the data shown in Fig.6. The root-mean-square deviation of the residual map is 424 counts/s

图8 图6所示数据的CLEAN算法处理结果,其残图的均方差为405 counts/s
Fig.8 Results of the CLEAN algorithm applied to the data shown in Fig.6. The root-mean-square deviation of the residual map is 405 counts/s

图9 图6所示数据的差分CLEAN算法处理结果,其残图的均方差为369 counts/s
Fig.9 Results of the Differential-CLEAN algorithm applied to the data shown in Fig.6. The root-mean-square deviation of the residual map is 369 counts/s
表2三种算法对IBIS数据的重建结果
Table2ReconstructionresultsofIBISdatawiththreealgorithms

残图均方差(counts/s)交叉相关算法424CLEAN算法405差分CLEAN算法369
4 多科学窗口的差分CLEAN
INTEGRAL在实际观测中,为了减轻本底对方向的依赖性,采用一种抖动观测的策略[18-19]:在一个方向观测一段时间后,就换一个方向重新观测。每次持续约30 min时间,这段时间的观测数据被集中到一起,称之为一个科学窗口(Science Window, SCW)。由于每个科学窗口的指向不一样,INTEGRAL现有软件的处理过程是首先对每一个科学窗口数据进行成像操作,然后把所有科学窗口图像叠加起来,以期探测到一些弱源。这样做存在一个明显的缺陷[20]:在每一个科学窗口图像中,由于背景噪声的存在,强源的旁瓣事实上不可能被完全扣除,弱源则完全淹没在噪声中,根本无法进行CLEAN操作。所以,目前数据分析软件在探测弱源方面的能力比较弱,即使在图像中发现了弱的结构,也很难确定它们的真实性。

图10 两组科学窗口的数据在天球坐标下的图像,观测起始时间分别为2004-09-04T20∶15∶52至20∶18∶03,2004-09-05T1∶34∶34至1∶37∶02,其余与单科学窗口差分CLEAN所用数据相同
Fig.10 The two SCW images (in overlapping) in the RA-DEC coordinates used for image reconstruction. The first observation lased from 2004-09-04T20∶15∶52 to 20∶18∶03, and the other lasted from 2004-09-05T1∶34∶34 to 1∶37∶02
为了克服这一缺陷,差分CLEAN算法首先将多科学窗口数据对应的交叉相关图进行叠加;然后在叠加后的脏图(或残余图)上进行CLEAN处理,获得一个统一的模型图像。之后,用统一的模型图计算各个科学窗口数据对应的模型阴影图,并求解其残余阴影图;最后,用多科学窗口数据的残余阴影图获得一个新的叠加后的残余图。如此反复,直到残余图中不存在明显的信号结构。这样做可以对每个科学窗口数据进行彻底的CLEAN,从而提高图像重建的质量。
由于图像的叠加必须在球面坐标下进行,为此首先需要得到单个科学窗口数据的脏图(或残余图)所对应的天球坐标。在统一的天球坐标系下将多个科学窗口的脏图结果拼接到一起(如图10)。接下来以拼接后的阴影图作为新的输入数据,可以使用差分CLEAN进行进一步的图像重建工作。
INTEGRAL多科学窗口数据差分CLEAN处理程序的开发工作量比较大,目前正在进行之中。等整个软件包开发、测试完成后,再公布程序及相关的研究结果。
5 总 结
把用于射电天文中改善合成孔径成像质量的差分CLEAN算法移植到编码板成像中, 使用差分CLEAN算法对IBIS编码板望远镜采集的数据进行图像重建。用交叉相关算法、传统CLEAN 算法及差分CLEAN算法进行的对比实验表明,差分CLEAN算法能有效消除鬼像,降低背景噪声,并规避对缺失数据的插值等处理引入新误差的问题。此外新算法还可以直接联合多个阴影图数据进行成像处理,大大增强成像灵敏度。这一方法能够更好地处理弱源的观测数据,以期获得更多的科学产出。
[1] E Caroli, J B Stephen, G Di Cocco, et al. Coded aperture imaging in X- and gamma-ray astronomy[J]. Space Science Reviews, 1987, 45: 349-403.
[2] Golay M J. Point arrays having compact, nonredundant autocorrelations[J]. Journal of the Optical Society of America, 1971, 61(2): 272-273.
[3] E E Fenimore, T M Cannon. Coded aperture imaging with uniformly redundant arrays[J]. Applied Optics, 1978, 17(3): 337-347.
[4] S R Gottesman, E J Schneid. PNP—A new class of coded aperture arrays[J]. IEEE Transsctions on Nuclear Science, 1986, 33(1): 745-749.
[5] A R Gourlay, J B Stephen. Geometric coded aperture masks[J]. Applied Optics, 1983, 22(24): 4042-4047.
[6] G K Skinner. Coded-mask imaging in gamma-ray astronomy[EB/OL]. [2011-11-20]. http://arxiv.org/abs/astro-ph/0302354.
[7] R J Proctor, G K Skinner, A P Willmore. The design of optimum coded mask X-ray telescopes[J]. Monthly Notices of the Royal Astronomical Society, 1979, 187: 633-643.
[8] J A Högbom. Aperture synthesis with a non-regular distribution of interferometer baselines[J]. Astronomy and Astrophysics, 1974, 15(2): 417-426.
[9] U J Schwarz. Mathematical-statistical description of the iterative beam removing t on. Ast. Ast A-RAY ASTRONOMY TALUCCI,echnique (method CLEAN) [J]. Astronomy and Astrophysics, 1978, 65(2): 345-356.
[10]G A Wagenknecht. A contour tracing and coding algorithm for generating 2D contour codes from 3D classified objects[J]. Pattern Recognition, 2007, 40(4): 1294-1306.
[11]G M Hunter. Operations on images using quad trees[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1979, 1(2): 145-153.
[12]I Gargantini. An effective way to represent quadtrees[J]. Communications of the ACM, 1982, 25(12): 905-910.
[13]U J Schwarz. Mathematical-statistical description of the iterative beam removing technique (Method CLEAN) [J]. Astronomy and Astrophysics, 1978, 65(2): 345-356.
[14]G K Skinner, T J Ponman. On the properties of images from coded-mask telescopes[J]. Monthly Notices of the Royal Astronomical Society, 1994, 267: 518-522.
[15]R C Puetter, T R Gosnell, Amos Yahil. Digital image reconstruction: deblurring and denoising[J]. Annual Review of Astronomy and Astrophysics, 2005, 43(1): 139-194.
[16]A Goldwurm, P David, L Foschini, et al. The INTEGRAL/IBIS scientific data analysis[J]. Astronomy and Astrophysics, 2008, 58(1): 1-8.
[17]INTEGRAL Science Data Centre. Introduction to the INTEGRAL Data Analysis[EB/OL]. [2011-11-20]. http://www.isdc.unige.ch/integral/analysis.
[18]E W Greisen, M R Calabretta. Representations of world coordinates in FITS[J]. Astronomy and Astrophysics, 2002, 395(3): 1061-1076.
[19]M R Calabretta, E W Greisen. Representations of celestial coordinates in FITS[J] . Astronomy and Astrophysics, 2002, 395(3): 1077-1122.
[20]崔辰州, 李文, 于策, 等. FITS数据文件的检索和访问[J]. 天文研究与技术——国家天文台台刊, 2008, 5(2): 116-123.
Cui Chenzhou, Li Wen, Yu Ce, et al. Search and location of FITS data files[J]. Astronomical Research & Technology——Publications of National Astronomical Observatories of China, 2008, 5(2): 116-123.
