EMCCD附加噪声对天文高分辨成像的影响*
2013-12-16张向波金振宇
张向波,金振宇
(中国科学院云南天文台,云南 昆明 650011)
对星体的高分辨率成像是天文观测的重要目标之一。高分辨统计重建技术是目前地面望远镜实现高分辨率成像的主要方法之一,可分为频域统计重建方法和空域统计重建方法两类。斑点干涉术[1]作为频域统计重建方法的典型代表,主要是通过对目标系列斑点图的功率谱进行统计从而实现目标的模或自相关的高分辨重建。为方便描述斑点干涉术重建方法,进行以下定义:目标为O(x,y),大气-望远镜瞬时点扩散函数为h(x,y),目标斑点图为i(x,y);其频谱分别为O(u,v)、H(u,v)、I(u,v)。在满足等晕性条件下
i(x,y)=O(x,y)⊗h(x,y)
(1)
I(u,v)=O(u,v)·H(u,v)
(2)
(1)式和(2)式中,x,y为空间坐标变量;u,v为空间频率坐标变量;符号⊗代表卷积算符;符号·代表乘积算符。遍历假设下,时间平均代替系综平均,目标斑点图的功率谱统计结果为:
(3)
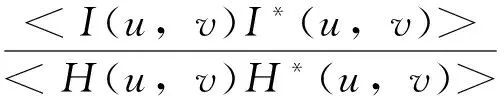
(4)
(3)式和(4)式中,<...>表示对其中的函数进行时间平均;*号表示取相应函数的复共轭;
高分辨统计重建技术的数据主要是冻结大气湍流的目标系列短曝光图像,获得信噪比高的目标短曝光图像是高分辨统计重建的首要工作。常规CCD中读出噪声小的其读出速度慢,难以获得短曝光图像;读出速度快的其读出噪声大,斑点图信噪比不高。增强型CCD(ICCD)虽然有电子倍增效应,可对入射信号实现放大,但是其量子效率低。电子倍增CCD(EMCCD)[2]是在常规CCD结构的基础上,在读出寄存器后又连续增加一串“增益寄存器”(全固态),实现信号放大。EMCCD采用超低温深度制冷减小暗电流,利用高的倍增增益(EM Gain)抑制读出噪声,可获得常规CCD无法比拟的信噪比。EMCCD又因其具有微光探测能力、高量子效率、高读出速率、有利于获得短曝光图像等特点,目前成功应用于暗弱目标的高分辨成像中[3-6]。EMCCD相对于常规CCD和ICCD虽然可获得信噪比高的短曝光图像,但是其附加噪声不同于常规CCD和ICCD,其附加噪声在天文目标观测中对斑点图信噪比及高分辨成像结果产生那些影响,尤其是当所观测目标非常暗弱时。本文在理论分析基础上通过模拟详细分析了EMCCD的附加噪声对天文目标高分辨统计重建技术——斑点干涉术传递函数信噪比的影响,并和实验进行了对比,同时对EMCCD附加噪声产生的偏差进行了改正。对观测数据利用斑点干涉术进行重建时,通过对噪声偏差进行改正,可以有效抑制噪声偏差对目标功率谱和自相关重建结果的影响,这样可更准确的测定双星的相对强度比。
1 EMCCD的附加噪声
EMCCD的附加噪声主要包括4方面:倍增噪声(Multiplication Noise)、暗电流(Dark Current)、时钟感生电荷(Clock Induced Charge, CIC)和读出噪声(Readout Noise)。
倍增噪声是入射光在EMCCD中实现倍增过程中产生的,它使光子噪声的方差增大为原来的两倍,这种噪声可用噪声因子描述。文[7]作者给出了噪声因子的表达式
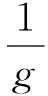
(5)
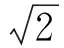
EMCCD的暗电流和常规CCD一样主要是在耗尽层内通过复合产生的暗电流SB和通过表面态产生的暗电流SS,其模型[8]分别为SB=3.3×106T2e-9 080/T,SS=122T3e-6 400/T。影响暗电流的主要因素是温度,通过深度制冷可以有效减小暗电流。
时钟感生电荷又称为假电荷,是在电荷转移过程中碰撞电离产生的,与积分时间无关。它可以在光电子由探测器的光照区向存储区垂直转移过程中产生(垂直时钟感生电荷),也可以在增益寄存器中产生(水平时钟感生电荷)。时钟感生电荷在常规CCD和EMCCD都出现,只是常规CCD中暗电流和读出噪声要比时钟感生电荷大得多,而EMCCD在高分辨成像时工作于高倍增增益、短曝光状态,所以读出噪声和暗电流很小。同时,对比图1中EM Gain=300和1 000时时钟感生电荷数据直方图,可以看出时钟感生电荷随倍增增益增大而增大,所以时钟感生电荷成为最主要的噪声因素。影响时钟感生电荷特性的因素很多,研究表明[9-11],时钟感生电荷随温度降低而减小,随帧频增大而增大,随EMCCD电荷转移速度增大而增大,与垂直转移频率成反比,随时钟上升时间增加而减小,随时钟电压增大而增大,并且时钟感生电荷的方差和增益寄存器的个数成正比,大致服从泊松分布。
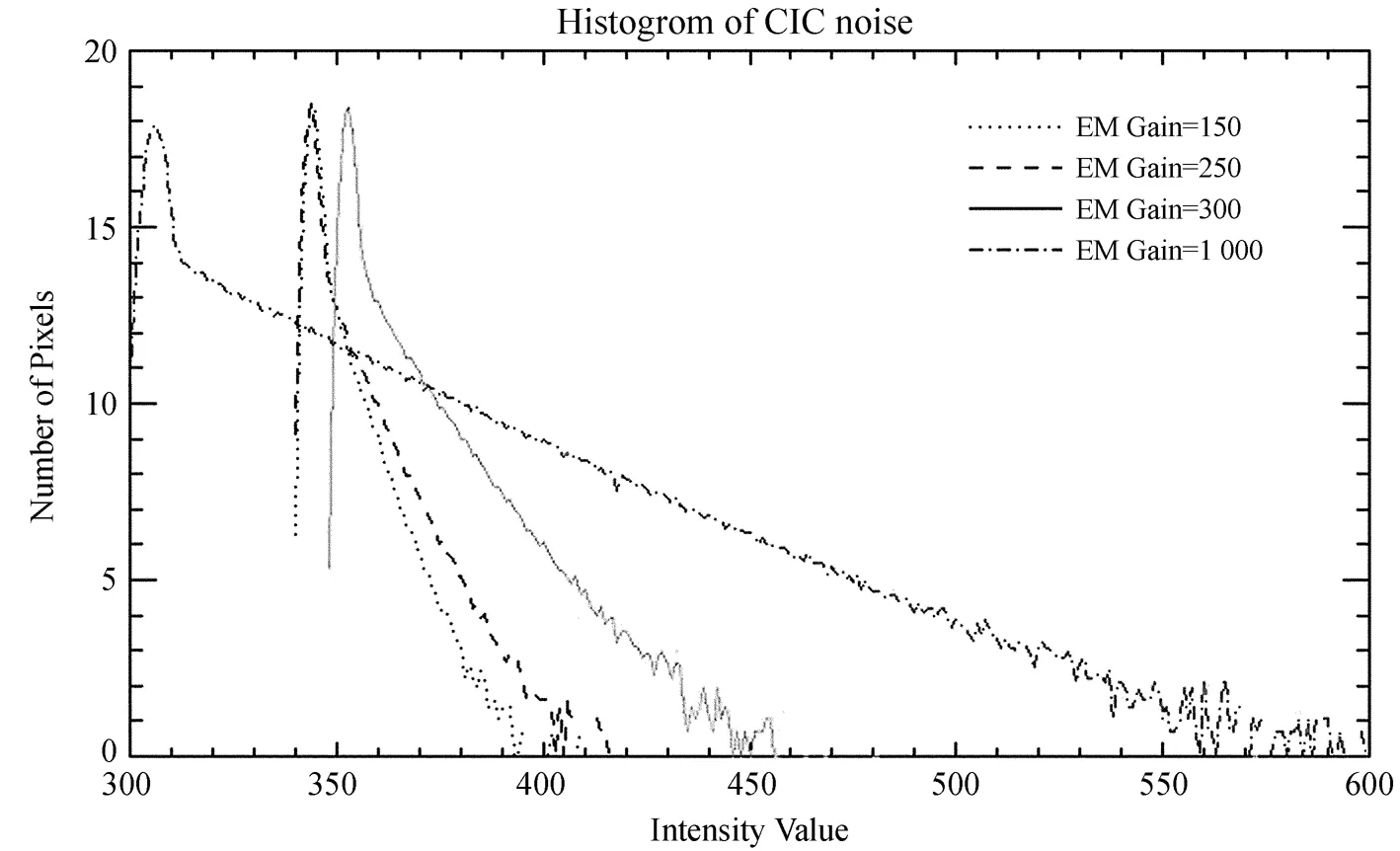
图1 时钟感生电荷随倍增增益的变化
Fig.1 Distributions of CIC for different EM-Gain values
EMCCD的读出噪声是在读出放大器中产生的,它本身和倍增过程无关,随读出速度增大而增大,通过高的倍增增益可以有效抑制读出噪声的影响,所以引入等效读出噪声[12],如下式:
(6)
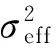
2 EMCCD附加噪声对高分辨统计重建的影响
2.1 附加噪声对斑点干涉术的影响
斑点干涉术传递函数是由点源单星瞬时点扩散函数的平均功率谱获得的。理想情况下,当点源单星较暗且斑点图中无附加噪声而只考虑光子噪声时,用经典的delta函数模型描述其强度为:
(7)
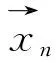
(8)
此时N幅斑点图功率谱平均后[13]功率谱为:
(9)
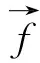
但是实际上,点源单星斑点图含有EMCCD的附加噪声,且附加噪声和信号是统计独立的,这时斑点图强度为:
(10)
其傅里叶频谱为:
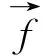
(11)
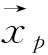
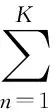
(12)
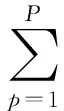
上式中*表示复共轭,最后两项为噪声和信号的相关,用N表示。最后求得附加噪声下斑点干涉术的传递函数的信噪比为:
(13)
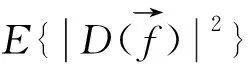
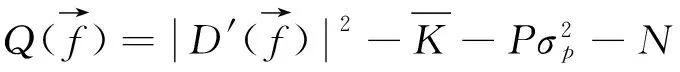
(14)
则噪声偏差改正后斑点干涉术的传递函数的信噪比为
(15)
(15)式中算符var{...}表示求方差。
2.2 数值模拟
为了验证以上附加噪声偏差对斑点干涉术的影响和噪声偏差改正模型的正确性,首先对云南天文台EMCCD(DU897)的附加噪声进行了实测,然后根据实测得出的量,模拟了附加噪声下点源单星斑点图,如图2,其中点源单星光子数为1 000,大气视宁度参数是10 cm,时钟感生电荷为0.013e-/pix/frame,读出噪声为54e-(这里e-表示电子),EM Gain=300,斑点图的CCD采样区域是256 pixel×256 pixel。同时,对模拟的斑点图加上了实测的附加噪声,最后分别求斑点干涉术的传递函数,对比分析理想情况下,实际噪声下的斑点干涉术的传递函数和模拟噪声下的斑点干涉术的传递函数,如图3。

图2 EMCCD附加噪声、大气-望远镜瞬时点扩散函数和附加噪声下的点源单星斑点图(a) EMCCD附加噪声; (b) 大气-望远镜综合系统瞬时点扩散函数; (c) 附加噪声下的点源单星斑点图
Fig.2 Images of additional noise of an Electron-Multiplying CCD, (a) image instantaneous synthetic PSF of atmosphere and telescope (b), and speckled star with EMCCD noise
首先,对比图3中附加噪声下的斑点干涉术的传递函数和理想情况下斑点干涉术的传递函数可发现,一方面,附加噪声产生的偏差使斑点干涉术的传递函数在中、高频相对理想情况下斑点干涉术的传递函数出现了很大的起伏,斑点干涉术的传递函数的中、高频方差变大,信噪比降低,最终导致难以重建接近望远镜衍射极限的高频信息。对暗弱目标来说,倍增噪声和时钟感生电荷成了影响斑点干涉术的传递函数信噪比的主要因素。
其次,对比实测噪声下的斑点干涉术的传递函数和模拟噪声下的斑点干涉术的传递函数,可以看出实测的EMCCD附加噪声是和实际情况吻合的,同时也验证了EMCCD附加噪声对斑点干涉术影响的正确性。
为了消除附加噪声偏差对斑点干涉术传递函数信噪比的影响,用(13)式对噪声偏差进行了改正,同时和常规CCD获得的斑点干涉术进行了对比。倍增噪声实质是光子噪声,因为它是入射光子的随机涨落,因此对光子噪声偏差的改正就是对附加噪声偏差进行改正。从图4可看出, EMCCD能对暗弱目标入射光子进行放大,可获得常规CCD无法比拟的信噪比。对比图3和图4可看出,在目标非常暗弱时用以上模型进行噪声偏差改正后,有效抑制了EMCCD附加噪声偏差对斑点干涉术的传递函数各频率信噪比的影响,基本解决了EMCCD附加噪声对斑点干涉术在重建目标自相关或模时的影响。
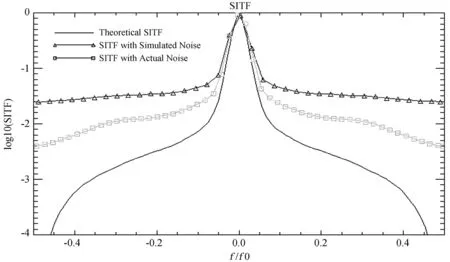
图3 斑点干涉术的传递函数随附加噪声的变化
Fig.3 SITF values at different levels of additional noise
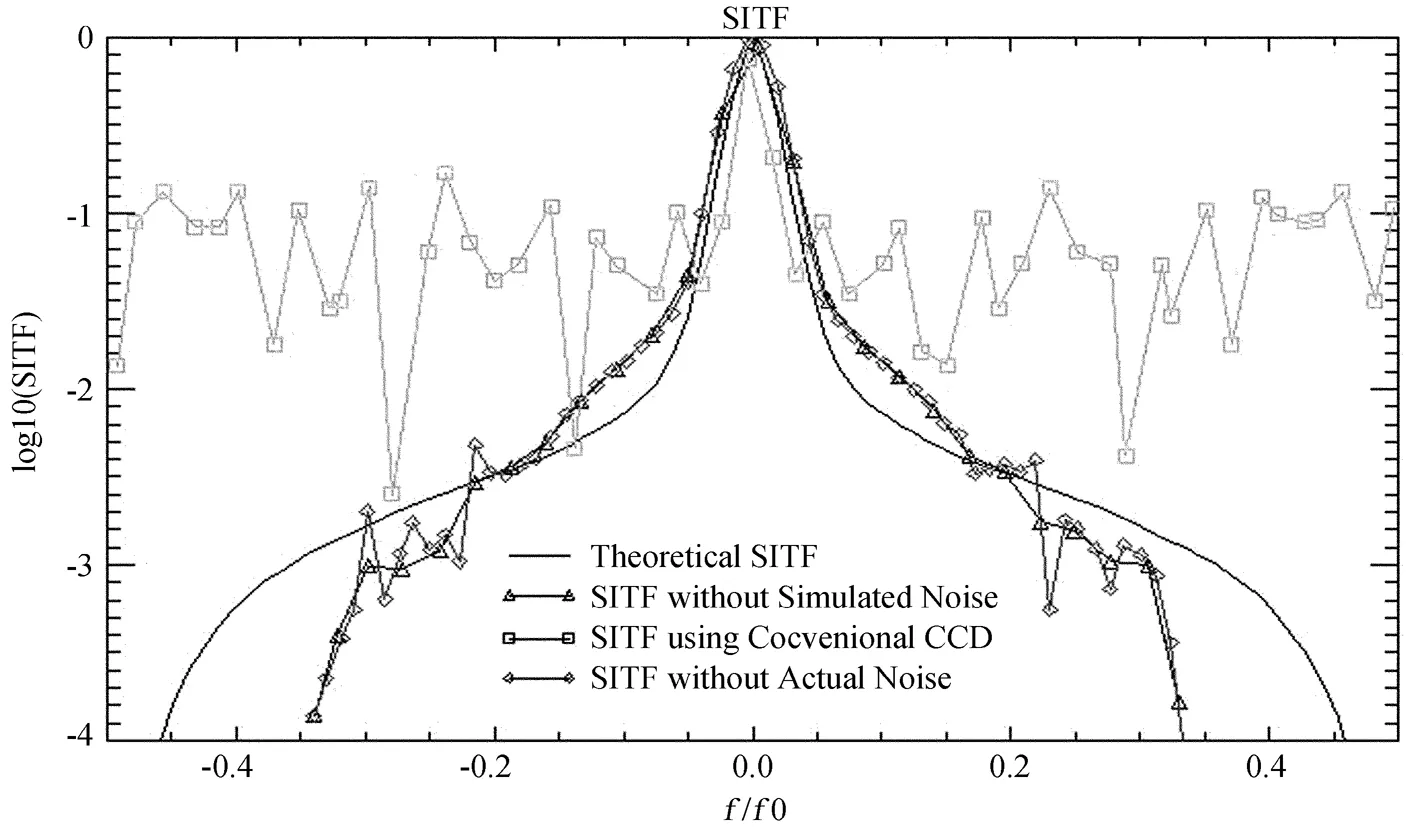
图4 附加噪声偏差改正后的斑点干涉术的传递函数
Fig.4 SITF values at different levels of additional noise after the bias correction
2.3 实测数据处理结果
2009年2月9日利用丽江2.4 m望远镜获得了大量的实测数据,其中双星HDS1574的主星可见星等为7.56 mag,伴星可见星等10.99 mag,星等差3.43 mag,最后观测时间为1991年。观测中采用了标准滤光片,每波段采集目标数据10 000幅,参考星数据5 000幅,图像大小256×256,采用4倍放大镜,EMCCD像元尺寸为16 μm×16 μm,每像素为0.043″。
对于一般暗弱目标,倍增噪声和时钟感生电荷成为影响高分辨成像的主要噪声,但是此时对于双星HDS1574,由于目标较亮,入射光子流量较大,倍增噪声相对于时钟感生电荷对重建产生的影响更大,所以此时倍增噪声成为影响EMCCD高分辨成像信噪比的主要因素。如果没有噪声偏差影响时,设双星强度为:
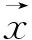
(16)
式中,d1和d2分别为主星和伴星的强度;x1和x2分别为主星和伴星位置;Δx=x1-x2为双星角间距。经过斑点干涉术重建得到目标的功率谱和自相关后,双星的相对亮度比d1∶d2可由下式得到:
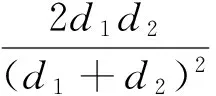
(17)
式中,(d1+d2)2表示双星相关峰主峰强度,旁瓣峰值强度为d1d2。但是有噪声偏差影响时,双星相对亮度比将难以准确测定。对噪声偏差进行改正后,利用斑点干涉术进行目标自相关重建,然后用理想望远镜光学传递函数(OTF)滤波后结果如图5,其中图5(a)为进行噪声偏差改正前后所获取的目标功率谱重建结果,图5(b)为对噪声偏差改正前后所获取的目标自相关重建结果。对比图5(a)中的噪声偏差改正前后目标功率谱重建结果可以很明显看出,未进行噪声偏差改正时,由于EMCCD倍增噪声引起的噪声偏差,目标功率谱高频出现了起伏,经过噪声偏差改正后,目标功率谱条纹的对比度提高,原本高频微弱的信息也得以体现。由功率谱条纹间距可以更准确测定主伴星间距。同时,对比图5(b)中的噪声偏差改正前后目标自相关重建结果,噪声偏差改正前主伴星相对亮度比为43.68∶1,噪声偏差改正后主伴星相对亮度比为31.89∶1,而双星真实强度比为31∶1,从而可以很明显看出,噪声偏差改正后主伴星相对亮度的测定可以更准确。
由此利用提出的噪声偏差改正模型对重建目标自相关或模时噪声偏差的影响进行了改正,基本解决了EMCCD附加噪声对斑点干涉术在重建目标自相关或模时的影响,可以更准确测定双星主伴星的相对亮度比和角间距。
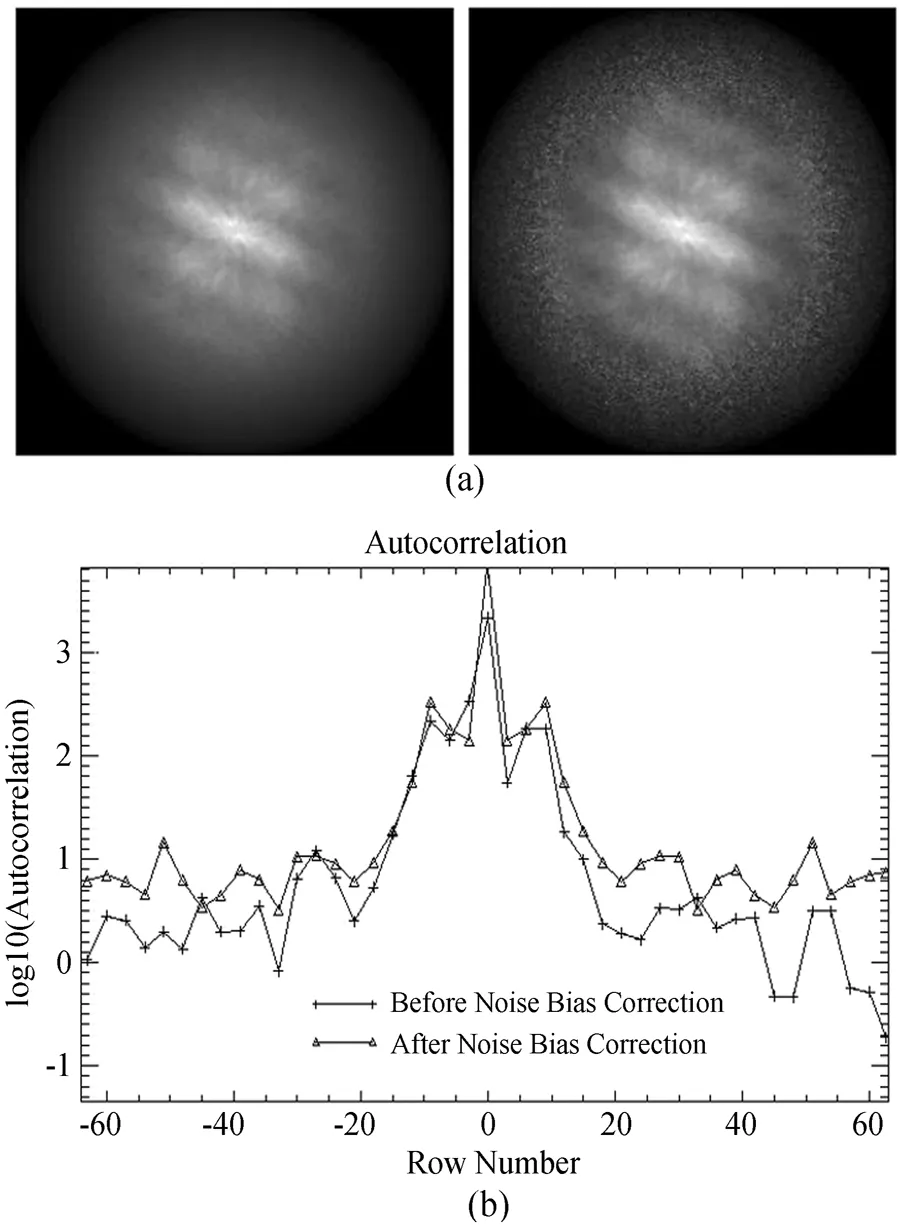
图5 附加噪声偏差改正前后斑点干涉术重建结果比较
(a) 附加噪声偏差改正前后目标功率谱重建结果比较;(b) 附加噪声偏差改正前后目标自相关重建结果
Fig.5 Comparison of Speckle-Interferometry results before and after the noise-bias correction
(a) Comparison of the power spectra of the object before and after the noise-bias correction; (b) Comparison of the autocorrelations of the object before and after the noise-bias correction
3 结 论
从EMCCD附加噪声特性的分析可以看出,当目标非常暗弱,在高倍增增益、高帧频、短曝光时,影响EMCCD高分辨成像信噪比的主要噪声就是倍增噪声和时钟感生电荷。模拟分析EMCCD附加噪声对斑点干涉术影响的结果表明,因附加噪声引入的噪声偏差,斑点干涉术传递函数中、高频信噪比严重下降。从噪声偏差改正的结果来看,所提出的噪声偏差改正模型基本解决了EMCCD附加噪声对斑点干涉术在重建目标自相关或模时的影响。
[1] A Labeyrie. Attainment of diffraction-limited resolution in large telescopes by Fourier analyzing speckle patterns in star images[J]. Astronomy and Astrophysics, 1970, 6: 85-87.
[2] A O’Grady. A comparison of EMCCD, CCD and emerging technologies optimized for low light spectroscopy applications[C]// Mahadevan-Jansen, Petrich, Wolfgang H. Biomedical Vibrational Spectroscopy III: Advances in Research and Industry. Proceedings of the SPIE, 2006, 6093: 183-191.
[3] A G Basden, C A Haniff, C D Mackay. Photon counting strategies with low-light-level CCDs[J]. Monthly Notices of the Royal Astronomical Society, 2003, 345(3): 985-991.
[4] F Hormuth, S Hippler, W Brandner, et al. AstraLux: the calar alto lucky imaging camera[J]. Proceedings of SPIE, 2008, 7014: 7873-7884.
[5] Robert N Tubb. Lucky exposures: diffraction-limited astronomical imaging through the atmosphere[M]. Cambridge: Cambridge University Press, 2003.
[6] N M Law. Lucky imaging: diffraction limited imaging from the ground in the visible[M]. Cambridge: Cambridge University Press, 2007.
[7] M S Robbins, B J Hadwen. The noise performance of electron multiplying charges coupled devices[J]. IEEE Transations on Electron Devices, 2003, 50(8): 1227-1232.
[8] E2V technologies. Low-light technical note 4: dark signal and clock-induced charge in L3VisionTMCCD sensors[EB/OL]. [2012-03-05]. http://www.e2v.com/e2v/assets/File/documents/imaging-space-and-scientific-sensors/Papers/low_light_tn4.pdf.
[9] Mackay C D, Tubbs R N , Bell R, et al. Sub-electron read noise at MHz pixel rates[J]. SPIE, 2001, 4306: 289-298.
[10]O Daigle, C Carignan, J Gach, et al. Extreme faint flux imaging with an EMCCD[J]. Publications of the Astronomical Society of the Pacific, 2009, 121: 866-884.
[11]O Daigle, C Carignan, S Blais-Ouellette. Faintux performance of an EMCCD[C]// David A Dorn,Andrew D Holland. High Energy, Optical, and Infrared Detectors for Astronomy II. Proceedings of SPIE, 6276: 62761F-62769F.
[12]Imag E M. EM-CCD Technical Note[EB/OL]. [2012-03-05]. http://www.photonicsonline.com/doc.mvc/EM-CCD-0001.
[13]Michael C Roggemann, Byron M Welsh. Imaging through turbulence[M]. CRC Press, 1996.
