路堤边坡变形与稳定安全分析

傅搏峰

(上海市路政局)

路基边坡在运营期和施工期都存在失稳安全隐患。路基工程在设计阶段是通过验算的方法对路基和边坡局部或整体稳定性进行校核，但是在施工和运营过程中，由于地质地形的复杂性、环境作用的随机性以及一些不当工程措施的原因，路基边坡失稳隐患依旧存在。所以，在施工或运营过程中对路基结构的整体稳定安全进行实时监控就显得尤为必要。

路基稳定性监控主要是通过对路基及边坡的变形进行监测而实现的。实际工程当中，一般通过埋设于路基土体内部的监测元件获取变形监测信息，元件埋设位置通常包括路基边坡的坡顶、坡脚、地基顶面及软土层内部等。对于获得的变形监测数据必须首先进行分析，然后制定相关的指标和标准进行评价，才能实现对路基稳定安全性态的监控和评价。

在路基工程施工阶段对路基结构进行变形监测以控制施工进度是较为普遍的做法。监测数据一般绘制沉降变形s－t曲线，然后制定某个定量的沉降速率控制标准(往往是通过经验确定的某个沉降速率值)来控制工程的施工进度。这种方法的特点是简单、实用，比较适合施工期监测单纯用于控制填土速率和保证施工安全。但是，同样的方法用于运营期的稳定性监控则并不合适，其局限性表现在:(1)评价指标过于简单:施工期路基稳定主要影响因素是填土加载，其他因素处于次要地位，而运营期路基稳定影响因素则较为复杂，因而单一的定量沉降变形控制指标和标准不能反映路基稳定状态变化的复杂性和时效性;(2)不能实现监测数据实时分析，难以对结构稳定安全性态进行动态监控和评价:运营期路基稳定性和结构变形都具有复杂性、时变性和不确定性，所以必须对路基结构变形和稳定性进行实时监控和评价才能保证运营中路基路面工程的整体结构安全。

针对以上问题和实际工程中的需求，必须建立能够用于运营期路基监测数据实时分析的监控模型，然后以监控模型为依据制定相关评价指标和标准，从而实现路基稳定安全性态的动态监控和评价。

1 路基时效变形监测信息的特征

路基结构监测中获取的是路基土时效变形监测信息。不同工况的路堤工程、不同位置的监测元件、复杂的地质气候及人为因素造成的随机性扰动会使监测到的变形数据体现出不同特征。通过对实测数据的总结分析发现，监测信息可分为四种基本类型:(a)平稳型;(b)发展型;(c)波动型;(d)混合型;各类型监测信息典型曲线形态如图1 所示。

图1 四种典型监测曲线形态特征

不同形态特征的变形监测信息所体现出的结构稳定安全性态各不相同。平稳型监测数据所体现的特征主要是变形随时间的增长变化较小，曲线形态基本保持稳定;通常该种类型监测信息所提示的边坡稳定安全性态处于非常良好的状态。发展型监测数据体现的特征主要是监测到的变形随时间变化有较为明显的增长趋势，如果变形加速发展则预示路堤边坡稳定安全性态趋于恶化，如果变形发展的速率逐渐收敛，则预示稳定安全性态趋于良好。波动型监测数据所体现的特征主要是数据离散性较大，变形随时间变化上下波动，较难看出其发展趋势;波动性较大的监测数据如果不是监测仪器的故障问题所造成，则说明路基土变形活跃，路堤边坡稳定性较差。混合型监测数据就是数据曲线体现出两种以上的特征，是前三种曲线形态的混合。

在实际工程中，平稳型监测数据一般出现在运营多年早已趋于稳定的路堤边坡的监测当中;发展型则有可能出现在各种工况条件下的填土或者填石路堤边坡，有时候填石路堤变形量要远小于填土路堤，其变形发展趋势不明显，监测数据表现出的形态会接近于平稳型;波动型和混合型监测数据一般出现在少数极不稳定的路段，另外也有可能路堤结构受到外界环境因素的随机扰动(地震、暴雨、附近人类工程活动等)所致。

目前，时效变形监测数据的建模方法主要有两大类:一类是通过数学模型回归拟合的方法绘制时变过程线，简称为“过程线法”;另一类是从数据自身规律出发，利用数理统计的方法建立分析模型。针对不同特征的时效变形监测信息，必须建立合适的监控模型，以下将分别建立适用于平稳型和发展型监测数据的“过程线”模型以及适用于波动型和混合型监测数据的统计学模型。

2 适用于分析平稳型及发展型监测信息的模型

通过数学模型拟合回归绘制实测数据的时变过程线是目前最常用的时效变形建模方法，平稳型及发展性监测信息的共同特点就是变形随时间发展趋势较为明显，比较适合于建立时变过程线模型。

由于路基边坡土体的时效变形是以岩土蠕变特性为基础的，并且体现出非线性特征，因此建立监控模型应当以基本的岩土蠕变公式为基础。目前，通过室内试验获得的经典蠕变公式主要有以下三种:(1)幂函数:y(t)=Atn;(2)对数函数:y(t)= ε0+ Algt;(3)指数函数:y(t)= A{1－ exp［f(t)］}。这几种典型的模型从不同数学关系的角度描述了时效变形的特征，但是单个的模型往往具有局限性，比如幂函数能够描述时效变形发展的规律，却无法描述变形收敛时的趋势;而对数与指数型模型可以表示非线性关系，但缺少表示线性关系的项源。因此，对于复杂的变形监测数据，为了提高监控模型的适应性，必须综合以上各基本模型的特点，建立多项源复合监控模型。基于以上分析，提出如式(1)所示的监控模型。

式中:St为变形量;t 为时间;a、b、c 为回归参数。

式(1)所示的监控模型从项源组成可以看出它可以很好的反映路基变形过程的线性及非线性特征。但是，影响路基变形的因素非常复杂，其中有相当一部分影响因素的影响方式表现为周期性。比如，交通荷载日夜周期循环作用，温度日夜变化，气温随季节周期变化，地下水涨落等。因此，可以考虑对以上模型加入反映周期性变化规律的项源进行完善。经过多次拟合，发现采用以下形式的周期项较为合适。

周期项中d、e 为待定系数，t0为常数，鉴于很多自然因素的变化都是以年份为周期的，因此，此处t0可取365;加入周期项的监控模型如式(3)所示。

式中:St为监测的时效变形;t 为时间;a、b、c、d、e 为均为回归参数。

采用吉林鹤(岗)大(连)江源镇监测试验工程中某高填方路堤监测数据对提出的模型进行验证，监测路段工况为季冻区软土地基高路堤，监测工程为施工期埋入监测元件并实现数据的自动采集和传输。采集的变形监测数据为该路堤边坡坡顶(测点编号YH2510A)竖向位移，监测时段为2009年10 月至2010 年8 月，经过对原始监测数据误差分析后选取该监测时段中100 个监测数据存入数据库待分析。

用模型拟合该段数据结果如表1 所示，拟合值与实测数据的比较如图2。从模型拟合回归的结果可以看出，加入周期项修正后的模型比原模型能够更好的拟合实测数据曲线:加入周期项的模型回归相关系数为0.947 明显高于原模型的0.709，从图2 也可以直观地看出，周期项修正后的模型比原模型拟合误差更小，更接近实测数据。

图2 模型拟合值与实测值比较

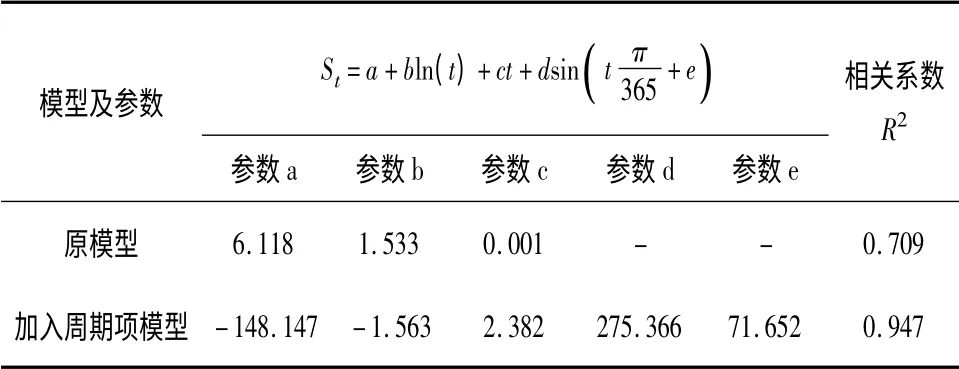
表1 模型拟合结果

根据获得的监控模型及时变曲线走势可以看出:2009年10 月至2010 年3 月这段时间边坡的变形发展趋势较为明显，4 月以后变形基本不再发展。这可能是因为试验路地处东北季冻区，路基土从10 月至次年3 月要经过一个逐渐冻胀的过程，因此监测到变形有所增加，但是由于变形增幅仅仅为5 mm 左右，应该不会对边坡稳定性有太大影响。

根据所建立的过程线模型可以拟定变形速率(ds/dt)以及变形加速率(d2/dt2)的指标，通过表2 所示判定标准检验变形速率的大小及加速率的符号即可评判路堤边坡的稳定性。分别计算以上两个监控指标，并绘制变形速率和变形加速率指标随时间变化过程线，如图3、图4 所示。从图3 及图4 可以看出，变形速率值(计为两次相邻读数间隔时间内发生的变形量)基本维持在较小的水平，最大值不超过2 mm;变形加速率的符号除了开始、结尾两端为正值(可能由于数据截取的“端部效应”造成)以外，中间大部分时间内都为负值。从监控指标可以判定，该路堤边坡稳定安全性态在大多数时段均处于一级或二级水平，总体稳定性良好。

表2 稳定安全评价标准

图3 变形速率变化

图4 变形加速率变化

3 适用于分析波动型及混合型监测信息的模型

波动型或者混合型监测信息往往含有离散性较大的监测数据，不适合绘制过程线，因此往往不能用模型回归的方法分析。图5 所示为用使用式(3)模型回归试验路中某路段测点所获取的波动型监测数据与实测数据的比较，从图4中可以看出，模型只能大致拟合出数据变化的方向，但是与实测数据的误差较大，模型相关性水平也很低。因此，对于波动型数据必须建立其它监控模型。

图5 式(3)模型拟合结果

路基变形监测数据(εi)由三个部分组成:初始变形量(ε)、时效变形量(di)以及测量误差量(δi)。其中，初始变形量是指岩土体不随时间推移而变化的那部分变形量;时效变形量是指随着时间推移而不断发展的那部分变形量;误差是指由于仪器的精度测量误差等原因造成的误差量，属于随机变量的范畴。四者关系可表示为

路基若处于时效变形状态，设在n 个时间节点发生的时效变形分别为w1、w2、wn，该时段内总的时效变形量为D =;设n 个时间节点的测量值分别为ε1、ε2、…εn，变形稳定值为ε0，则设ε1、ε2…εn均值为，样本方差为

各测量值与均值的差方为

求和:

当岩土体处于时效变形状态时，可以认为各时间段内发生的变形量相等，即w1=w2=… =wn=d，D =nd;代入上式可得

此时，样本方差为

假设n 个时间节点中的测量值分别为ε1、ε2…εn;对应的测量误差为δ1、δ2…δn;测量误差相互独立且服从正态分布N(μ，σ)，其方差为。因此，若考虑误差项，则样本方差应该为

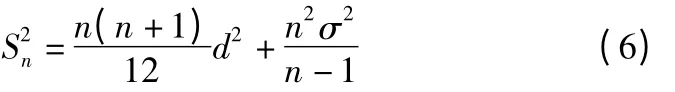
标准差应该为

同理，当路基处于稳定的状态时，意味着路基土体时效变形量可以忽略不计(既di≈0)，位移测量值的波动仅由测量误差引起。那么令式(4)中D=0，监测数据的标准差可表示为

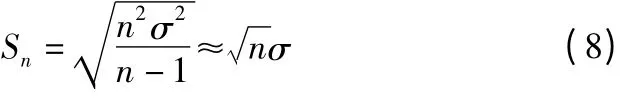
根据以上分析，可采用监测数据的标准差Sd作为监控指标，并且假定路基变形处于稳定状态的指标上限为Sd1=;边坡处在明显时效变形阶段的指标下限为Sd2=，从而划定“区间”评判标准对监测数据所反映出的稳定安全性态进行评判。根据计算出的监测数据标准差所处的区间位置对路堤边坡稳定安全性态分级评判标准如表3 所示。

采用以上所建立的统计学模型及评价指标对图5 中某开挖工程的高填方路堤变形实测数据进行分析。监测时段为2009 年10 月至2010 年8 月，分析所采用的数据取为100个，并且按照时间顺序每10 个数据一组，将全部时段100 个数据划分为十个时间段(各时间段分别标记为T1，T2，…，T10。根据表2 提供的监控指标和评价标准考察这十个时间段中监测数据所体现的边坡变形稳定状态，实现对结构的稳定安全性态进行全过程动态评价，评价结果如表4 所示。

图6 评价结果与实测数据对比

图6所示为各时段评判结果所对应的监测数据波动情形，结合表4 的评判结果可以看出:评价结果基本与各时段实测曲线波动性及走势相吻合。从建模及评价结果来看，2009年10月至2010年8月该路堤边坡稳定性并不非常良好:10 个时段的稳定安全评价结果中有五个时段是二级(异常)，并且有一个时段出现了三级(不稳定)，只有四个时段是一级(稳定)。前五个时段稳定性较后五个时段稳定性要差，其原因可能是2009 年10 月至年底(前五个时间段)由于边坡附近开挖而处于明显的卸荷变形阶段;后面随着工程完工，路堤边坡变形波动及增长的趋势放缓，稳定安全性态在一定程度上趋于良好。

表4 边坡稳定安全评价结果

4 结 论

从实际工程中获取的四类典型形态的监测信息特征出发，分别建立了不同的监测数据分析模型，然后针对提出的模型制定了稳定安全评价指标及标准，并且对试验路工程中所获取的监测信息进行分析，得出了监测路段路堤边坡稳定安全性态的动态变化情况。通过以上研究，可以得出以下结论。

(1)不同特征的路堤边坡变形监测信息，其数据的变化规律差异较大，反映的路堤边坡稳定安全性态也各不相同，因此不能采用同一种数据分析模型。

(2)所建立的两种监测信息分析模型当中，“过程线”模型适用于平稳型和发展型监测数据的分析;统计学模型适用于波动型和混合型监测数据的分析。两种模型及制定的相关评价指标、标准，从不同的角度对监测数据所反映出的路基边坡稳定状态及发展趋势进行了描述和判定。通过在试验路工程中的应用可以证明，模型能够用于运营期路基边坡稳定安全性态的动态监控与评价。

(3)过程线模型可以用于分析波动性较小的监测数据。加入反映周期性项源修正后的过程线模型较修正前的模型，其相关性水平及拟合精度均有所提高，因而是一种值得推荐的较佳监控模型。

(4)过程线模型不能用于分析波动型监测信息，提出的统计学模型及监控指标可以很好的分析和监控不同时段路堤边坡变形和稳定安全性态的动态变化情况，因此是分析离散性较大监测数据的适用模型。

［1］ 中华人民共和国行业标准.公路路基设计规范(JTJ 013－95)［S］.北京:人民交通出版社，1994.

［2］ 洪毓康.土质学与土力学［M］.人民交通出版社，1990.

［3］ 《岩土工程手册》编写委员会. 岩土工程手册［M］. 北京:中国建筑工业出版社，1994.