基于运动学的汽车悬架多目标优化方法探讨

孙明浩，王 金，侯志国，桂 军

(1.辽宁工业大学汽车与交通工程学院;2.安徽长丰扬子汽车制造有限责任公司)

1 前 言

悬架是汽车的重要组成部件，汽车行驶中，由于路面不平或车轮垂直载荷的变化，导致车轮定位参数的变动，将影响整车性能。车轮跳动过程中，必须保证车轮定位参数在合理范围内变动，因此，在设计中常需要对悬架进行运动学方面的优化。

在以往的设计中，工程师们常凭借个人经验通过试凑来调整各设计硬点的坐标，以达到悬架性能的设计要求，这种方法费时、费力，已经远远不能满足现代汽车设计要求。

随着计算机技术的发展以及各种先进算法的应用，国内外学者在悬架运动学优化方面取得了一定的进展，为提高整车性能提供了可参考的经验。

主要阐述了如何找出影响悬架运动学性能的因素，即优化问题中的设计变量，分析了近年来研究人员提出的几种悬架运动学优化方法，并比较其各自的优缺点，为更好地选择悬架优化方法提供参考。

2 悬架运动学优化问题的描述

2.1 基本概念

悬架运动过程中，如果悬架性能参数的变化不满足设计要求，可对相应硬点坐标进行调整，这是现代悬架设计和开发中常用的方法。

一个完整的悬架运动学优化问题包括设计变量、目标函数及约束条件。设计变量主要是指悬架导向机构、转向横拉杆等涉及到的硬点坐标。目标函数主要指悬架定位参数，包括外倾角、主销内倾角、主销后倾角以及前束角等。约束条件主要指设计变量和目标函数的变化范围，设计变量的约束条件主要依据悬架所占的空间范围以及考虑其调整给整车质心位置、轮距、轴距等基本参数带来的影响，故其变化范围不能过大;目标函数的约束条件一方面主要依据汽车设计中对定位参数等的变化范围及变化趋势的推荐值，另一方面也要根据具体设计要求进行一定范围上的限制。

2.2 优化过程

一个完整的悬架运动学优化过程包括:悬架的运动仿真及结果分析、设定设计变量及目标函数、给出约束条件、选择优化方法、根据优化结果再次进行运动仿真、最后得出优化前后悬架运动学性能对比。悬架系统运动关系比较复杂且直观性差，优化时设计变量涉及多个硬点坐标，目标函数也涉及多个定位参数。所以，悬架优化是一个多因子、多目标优化问题。

3 设计变量的选择

3.1 选择的依据

在优化问题中，设计变量的选择非常重要。首先，所选的设计变量要与目标函数之间存在一定的关联度(对目标函数影响的显著程度)，若关联度过低甚至不存在关联，将导致优化结果不理想甚至失败;其次所选的设计变量数量要合适，设计变量选择的多少意味着优化过程的复杂程度，若选择的过多，则会导致计算工作量大、太过繁琐，同时也没有必要，同样过少，也会导致优化结果不理想。

由上述分析可知，设计变量需要进行一定程度上的筛选，找出关联度高且数量合适的设计变量。

3.2 选择的步骤

目前，设计变量的筛选可以按以下步骤进行。

(1)设计变量的初步筛选。

假设所有硬点个数为n，要从中初步筛选m 个，则初步筛选出来的设计变量为其坐标个数3 m。初步筛选主要依据以下几方面进行。

①定位参数的定义表达式。

以麦弗逊独立悬架中的主销后倾角为例，其定义表达式为

式中:A 点为减震器上体与车身连接的万向节;E 点为转向节总成与下摆臂连接的球铰，如图1 所示，字母下标代表其坐标。

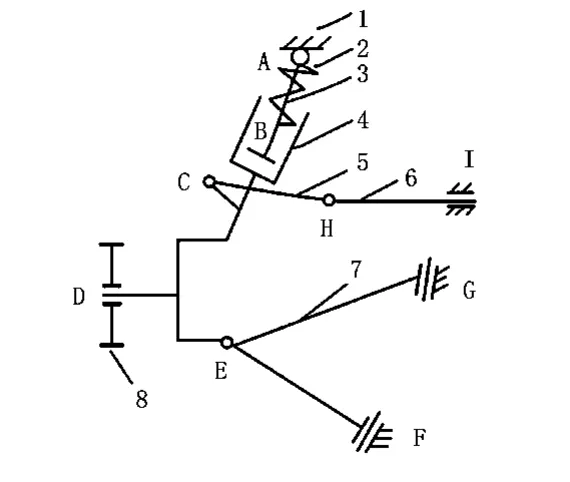
图1 麦弗逊悬架结构示意图

从主销后倾角定义表达式可知，A、E 两点的空间位置会直接影响主销后倾角的大小，所以，要将这两点设定为设计变量。

②前人通过试验得出的规律。

文献通过大量对比试验，得出了双横臂悬架导向机构设计参数的调整对车轮定位参数等的影响规律，以前束角为例，加长转向横拉杆可使横拉杆绕转向梯形断开点转动半径加大，以减小对车轮的拉动作用，进而对前束角产生影响。因此，目标函数含有前束角时，设计变量应包含转向横拉杆的内、外硬点坐标。

(2)设计变量的最终确定。

通过灵敏度分析确定设计变量的方法在悬架运动学优化中使用的较为广泛。灵敏度分析就是研究对目标函数影响最大的变量，是进行优化的一个有效工具。现在，研究人员主要是利用多体动力学软件ADAMS/Insight 对设计变量进行灵敏度分析，分别得到初步筛选的3 m 个设计变量对目标函数影响的显著度，然后从分析结果中选择p(p≤3 m)个影响较大的作为最终设计变量。

4 优化方法的分析与比较

4.1 主要目标法

根据实际情况，确定一个目标为主要目标，其余目标为次要目标，再根据决策者的经验，选取一定的界限值，把次要目标作为约束来处理，将原多目标问题转化为一个在新的约束下，求解主要目标最优解的单目标优化问题。

在悬架实际设计中，经常会遇到一项性能参数严重偏离设计要求，而其他几项性能参数则满足设计要求的情况，这时可以选择主要目标法进行优化。以前束角优化为例，研究表明:转向梯形不影响主销后倾角和内倾角的变化，对车轮外倾角和轮距的变化影响也很小，但对前束角的变化影响很大。对转向梯形断开点位置优化后，能明显减小车轮前束角变化量，减小轮胎磨损。因此，当遇到前束角严重偏离设计要求的问题时，可以考虑将前束角作为主要目标，而其他定位参数则作为次要目标进行优化。

主要目标法的优点在于优化时针对性强，能够较大程度地对主要目标进行优化，而对其他设计目标影响较小;其局限性在于只能适用于单一目标较为突出的多目标优化问题，且优化时对其他设计目标产生的影响要控制在合理变化范围内。

4.2 加权和法

加权和法是给多个分目标分别乘以一组权系数，然后相加作为目标函数，再对其求最优解。

加权和法在悬架运动学优化中应用的较为广泛，其重点在于确定设计变量后，如何为各分目标确定加权因子。以车轮定位参数及轮距变化五个量作为分目标为例，总的目标函数表达式为

式中:y1，y2，y3，y4，y5分别代表车轮外倾角、主销后倾角、主销内倾角、前束角及轮距的目标函数。ωi(i =1，2，3，4，5)为各分目标的加权因子。

目前，研究人员主要从以下几个因素来考虑各分目标的加权因子。

(1)以容限和平方倒数作为加权因子。

已知yi的取值范围为

则称

为该指标的容限，则该分目标加权因子为

采用这种取加权因子的方法，当某项分目标的数值变化范围越宽时，其目标的容限就越大，加权因子就取较小值;而当数值变化范围越窄时，目标的容限就越小，加权因子就取较大值。该方法可以达到平衡各分目标数量级的作用。

(2)依据分目标重要程度确定加权因子。

在多目标优化中，凡要求优先达到的目标应赋予较大的加权因子，使其在优化过程中有更大的优先权，即首先保证该目标的实现;而加权因子较小的目标是在实现加权因子较大的目标基础上考虑的;以此类推，由于外倾角和前束角直接影响汽车的直线行驶能力，对汽车操纵稳定性影响较大，应取较大权重;轮距变化对轮胎磨损有较大影响，也应取较大权重，其他分目标的权重可适量减小。

(3)根据设计侧重性能的不同确定加权因子。

针对侧重性能的不同，各分目标加权因子应有所区别。如:高速行驶的轿车对操纵稳定性的要求很高，因此应加大ω2、ω3、ω4的值。对于不同类型的轮胎，加权因子ω5的值也应有所区别。如:昂贵的防弹轮胎、低压、子午线轮胎，应加大ω5;而高压、斜交轮胎，可适当减小ω5。具体情况应根据轮胎的价格、使用寿命等因素来确定。

(4)采用各目标函数优化率决定权重大小。

加权和法重点在于确定各分目标的加权因子，文献提出一种新的计算加权因子的方法，即采用各目标函数优化率决定权重大小，它可以反映出加权和法优化过程中，目标函数向最优解的收敛速度，如果某目标函数在单一目标优化过程中变化较大，表示其收敛速度较快，那么在加权和法优化时乘以较大的权重，以表明其重要性。

优化率=(初始解—最优解)/初始解加权和法方法简单，求解速度较快，在悬架运动学优化中应用的较为广泛，在实践中，也能达到较为理想的优化结果;其缺点在于，悬架运动学分析较为复杂，其派生出的优化问题常常具有非凸、非线性、多峰、多维度等特点，而采用加权和法求解可行域为凹形的多目标优化问题时会出现优化解局部收敛。

4.3 基于Pareto 最优的多目标优化

Pareto 最优的多目标优化方法所求得的优化结果不是一个优化解，而是一组优化解，即优化解集，且各个优化解的优劣无法比较，设计人员可以根据具体的设计目标从优化解集中选择一组相对最优解用于悬架运动学优化。文献利用NSGA－II 算法求出悬架系统参数多目标优化的Pareto 最优解集，减少了车轮定位参数在车轮跳动过程中的变化量，从而既保证了车辆在行驶过程中的操纵稳定性又减小了轮胎的磨损速度。文献利用NSGA－II 算法对多连杆悬架跳动过程中车轮前束角、车轮外倾角和车轮侧向滑移的变化进行了优化，获得了三目标Pareto 最优解集，使多连杆悬架的运动学特性得到明显改善。

另外，文献分别利用主要目标法、加权和法以及Pareto最优法对悬架参数进行多目标优化并对优化结果进行了比较，发现用主要目标法求得的最优解只是Pareto 最优上的特殊点，而采用加权和法获得的最优解也是Pareto 最优上的一个解，它只是考虑了各目标函数之间的权重关系，综合权衡悬架的性能对悬架参数的要求。虽然文献主要是利用这三种优化方法针对悬架动力学进行了多目标优化而得出上述结论，但就优化方法的本质而言，上述结论同样适用于悬架运动学优化。因此，Pareto 最优法在悬架多目标优化中具有较高的参考和应用价值。

5 结 论

本文介绍的三种悬架运动学优化方法中，主要目标法适用于单一目标较为突出的多目标优化问题，具有一定的局限性;加权和法能够满足绝大多数的悬架运动学优化问题，过程简单，应用广泛;Pareto 最优法可提供最优解集供设计人员从中选择最符合设计要求的最优解，为更高要求的悬架运动学优化问题提供了解决的新思路。由于受到车身布置的限制，对硬点坐标的改变只能局限在一定的小范围内，所以，无论使用哪种优化方法所得到的最优值也只是一个相对值，而非绝对的最优结果。

［1］ 廖永升，刘拥军等. 基于ADAMS 的麦弗逊悬架运动学优化［J］.科学技术与工程，2012，12(20):4935－4950.

［2］ 周红妮，冯樱，李向阳.基于ADAMS 的汽车前悬架仿真分析及优化方法研究［J］.湖北汽车工业学院学报，2010，24(3):5－14.

［3］ 汤靖，高翔，陆丹.基于ADAMS 的麦弗逊前悬架优化研究［J］.计算机辅助工程，2006，(5):32－34.

［4］ 李瑜婷，赵治国，章桐.基于ADAMS 的双横臂悬架性能多目标优化研究［J］.中国制造业信息化，2009，(17):30－48.

［5］ 宋晓琳，毛开楠等.麦弗逊前悬架硬点参数的灵敏度分析和优化［J］.现代制造工程，2011，(6):106－110.

［6］ 龙岩.双横臂悬架专家系统导向机构知识体系的建立［D］. 长春:吉林大学，2008.