瑞典条分法检算路基边坡稳定性

勾文豹

(牡丹江市路桥公司)

圆弧条分法检算如图1 所示。假定滑动体ABC 是一个整体，沿着AB 假想圆弧面作整体滑动，因为这种滑动是滑动体绕圆心O 向下转动，故沿滑动面滑动的条件可用抗滑力矩与路基疆支挡结构滑动力矩的比值K 来表示，即

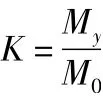
式中:My为阻止滑动体沿AB 面滑动的抗滑力所产生的力矩;M0为引起滑动体沿AB 面滑动的滑动力所产生的力矩;K 为稳定系数。

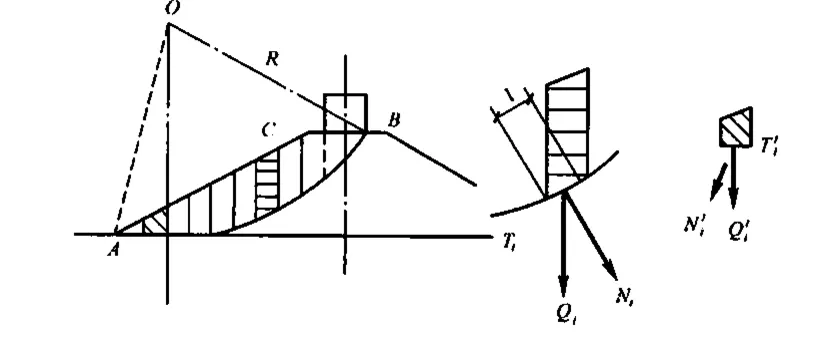
图1 圆弧条分法检算图

如果K ＞1，则表明抗滑力矩大于滑动力矩，边坡是稳定的，假想的滑动体不会产生。

如果K ＜1，则假想的滑动体将会形成井向下滑动。

如果K=1，则滑动体处于临界状态。

实际上，由于假定滑动土体沿圆弧面滑动，且将滑动体看作整体，检算中所采用的土的强度指标不能完全反映实际情况，考虑一定的安全储备，边坡稳定系数的最小值Kmin应满足1.15 ～1.25 的规定值。如所设计的边坡能满足这一要求，即认为边坡是稳定的。

用假想的圆弧滑动面进行边坡稳定性检算时，求My和M0数值的步骤如下。

沿线路纵向取1 m 殴的路堤土体作为计算单位，假定滑动圆弧通过A 点及B 点，在断面图上画出假定的滑动圆弧的位置，并将滑动土体分成若干直条。直条宽度一般不超过2 ～4 m，对路基横断面轮廓变化处或土的性质变化点、地下水位与圆弧的交点要进行分条，直条分得越密，计算结果越精确。假设备直条之间并不互相传递应力，则通过备直条重心作用于滑动面上的土条重量Qi可分解为与滑动面垂直的法向分力Ni和切向分力Ti，即

式中:αi为对第i 条土重心铅垂线与滑动圆弧交点所作的切线与水平面间的夹角。

将各直条作用于相应滑动圆弧段上的力，即Ntanφ、ciLi和Ti，分别乘以力臂，可得绕圆心转动的抗滑力矩∑My和滑动力矩∑M0，即

由此得

式中:∑T'i为圆心铅垂线以左部分的土条的切向分力，其作用方向与滑动方向相反而成为抗滑力矩。

从上式可以看出，∑Miy越大，边坡土体越稳定，当假想的滑动体抗滑力矩不足以阻止下滑力矩时，可考虑改缓边坡坡度值，使滑动力矩小于抗滑力矩，以满足边坡稳定的要求。

用圆弧滑动面法作边坡稳定检算时，需要寻求危险圆弧滑动面在路堤内形成部位，并寻求与危险圆弧滑动面形成部位相应圆心点的规律。由于圆弧滑动面的形成与许多因素有关，因此需要寻找一些规律简化计算。据经验可知，在一般路堤的情况下，危险滑动圆弧的圆心与圆弧位置有如下规律可供参考。

危险圆弧的形成与堤身填料的性质、边坡的形式、坡度和地基条件等有重要关系，当地基的承载力低，包括地基土的强度低于堤身填料的强度时，路堤的危险圆弧常可切入地基内，圆弧滑动面可能在坡脚以外出现，此圆弧称为坡底圆。在地基稳固时，堤身内的滑动圆弧下端常出现在坡脚，此圆弧称为坡脚圆。圆弧滑动面的上端，对于单线路堤，常以换算土柱的外侧边线与路基面交点为端点(轨枕点)，危险圆弧的端点可能向换算土柱内移动(路基中心点)，也可向外侧路肩移动(路肩边缘)，直至路肩边缘下的边坡上部，它与填料的性质和堤身高度有关。双线路基的危险圆弧端点在填料强度较高时会向两线的中部移动。但在填料强度较低时，危险圆弧的端点仍可出现在与单线路堤相似的部位。危险圆弧的半径与地基良好与否和路堤填料性质有关。

危险圆弧的圆心位置应和危险圆弧位置的出现部位相对应，在边坡稳定检算中，在简单土坡的条件下，危险圆心的辅助线(轨迹线)，可近似地从换算土柱高顶缘，作一水平面，再作与水平线成36°角的直线，则可认为路堤滑动时蛙小稳定系数的圆心在这条36°线上，此线称为最危险圆心的辅助线。

借助于最危险圆心辅助线，用上述检算方法可求出圆心辅助线上四个圆心O1、O2、O3、O4相应的稳定系数，用同一比例尺作K1、K2、K3、K4垂直圆心辅助线，得四点并连成K曲线，作圆心辅助线的平行线切K 曲线于一切点，切点处作圆心辅助线的垂线，其长度即为Kmin。与圆心辅助线的交点O 即为最危险圆弧的圆。

用圆弧条分法作边坡稳定检算，可以得到应用精度的数值，所以是一种获得公认的计算方法，但在理论上并不完善。例如，它认为滑动圆弧面上的土体路基及支挡结构作整体滑移，因此，把滑动圆弧面上的土体分为若干土条，仅为得出在圆弧面上滑动体的重力作用的分布状态，井据此检算滑动体的整体稳定性，它不考虑在把滑动体分为若干土条后，如果滑动而上有一土条的下滑力大于抗滑力，则为使滑动体保持整体滑动的条件，此土条和其相邻的上条之间原有的力平衡条件将改变，并且应在不出现剪切变形的条件下形成新的平衡。在条间力出现变化的情况下，各分条在滑动面上的作用也将改变。因此，在路基检算边坡稳定性时要求稳定系数Kmin大于所规定的稳定系数，即Kmin=［K］，所以，圆弧条分法是对条间力作用的简化，尚不影响其在工程应用中的可靠性。