典型混沌系统的吸引子和功率谱研究

孙红章，汤正新，刘钢，魏荣慧，苏向英，刘磊

(河南科技大学物理与工程学院，河南洛阳 471023)

0 引言

自然界中存在无数的无序、非平衡和随机的复杂系统．非线性动力学中提出的混沌理论透过扑朔迷离的无序混乱现象和不规则形态，揭示隐匿在复杂系统内部的规律［1］．自然界面对的更多的是非线性问题．混沌已经成为目前非线性科学研究中的热点问题［2－4］，Lorenz系统［5］、Henon 系统［6］和 Chen 系统［7］是典型的混沌系统．

1 功率谱的计算方法

功率谱分析是研究时间序列所遵从的统计规律的方法．研究一个系统的混沌行为，常用功率谱分析的方法，它揭示出了确定论系统内部的随机性．在很多实际问题中，人们常常能观测到如下的等时间间隔的离散时间序列:x1，x2，x3，…，xN．它反映了实际非线性动力系统的运动状态，而吸引子正是这种状态的归宿，因此吸引子的信息也包含在这一时间序列中．功率谱分析实际上是通过将时间空间转化为频率空间来阐明时间信号的频率结构的．对这个序列加上周期条件xN+j=xj，然后可计算时间序列xj的自相关函数(即离散卷积)

再对cj作傅里叶变换，其傅立叶系数

其中pk代表第k个频率分量对xj的贡献，这就是功率谱本来的含义．当发明快速傅里叶变换算法后，更有效的计算功率谱的方法便是不经过计算自相关函数，而是直接计算xj的傅里叶系数，

然后计算

一个时间序列可看做各种周期运动的叠加，各周期的的振动能量的分配pk即为功率谱［5］．离散时间序列的功率谱是实验可以直接测量的，因此功率谱分析是一个方便的工具．

2 典型混沌系统的吸引子和功率谱

2．1 Lorenz系统

Lorenz方程如下:

取σ =10，r=28，b=8/3．我们利用MATLAB软件中的Ode45(四五阶龙格 －库塔法)命令来对非线性Lorenz方程求解，并计算其功率谱，得到的洛仑兹系统的混沌吸引子如图1所示，其x分量的功率谱如图2所示．

图1 洛仑兹系统的混沌吸引子

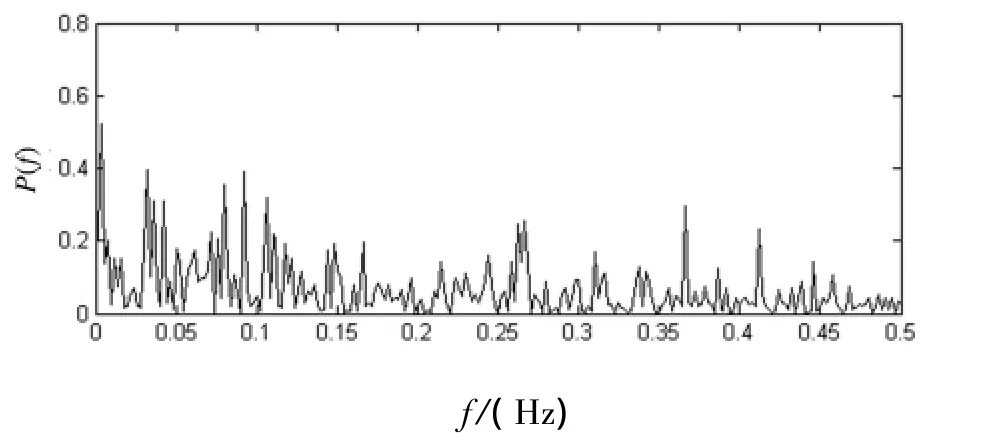
图2 洛仑兹系统x分量的功率谱

2．2 Henon 系统

Henon系统的动力学方程为:

取a=0.4，b=0.3．我们利用MATLAB软件对非线性Henon系统的动力学方程求解，并计算其功率谱，得到的Henon系统的奇怪吸引子如图3所示，其x分量的功率谱如图4所示．

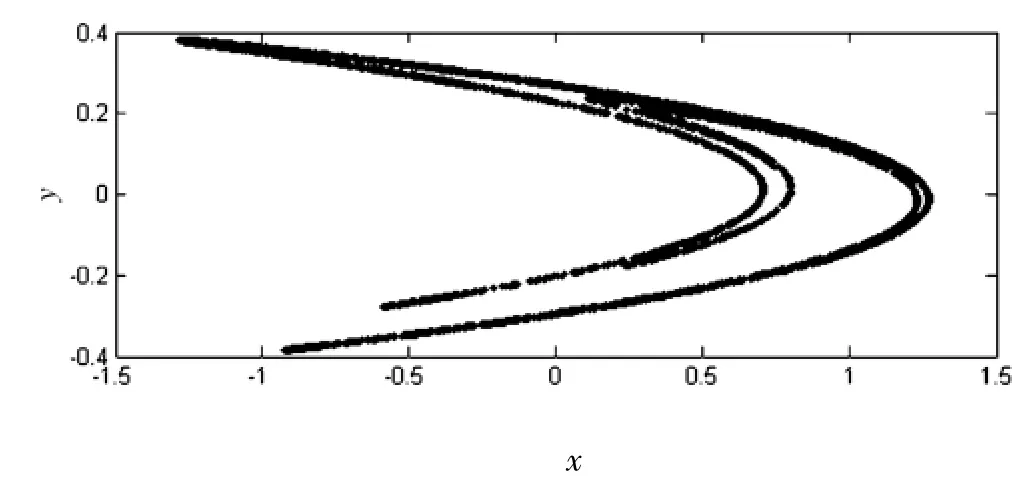
图3 Henon系统的混沌吸引子

图4 Henon系统x分量的功率谱

2．3 Chen系统

Chen系统的动力学方程为

取a=35，b=3，c=28．我们利用MATLAB软件对非线性Chen系统的动力学方程求解，并计算其功率谱，得到的Chen系统的奇怪吸引子如图5所示，其x分量的功率谱如图6所示．

图5 Chen系统的混沌吸引子

图6 Chen系统x分量的功率谱

3 讨 论

混沌运动的相轨迹局部不稳定，但全局稳定，相轨迹一般有两个稳定平衡位置，围绕一个稳定平衡位置振动若干次以后，转而围绕另外一个稳定平衡位置振动若干次，然后又跳回原平衡位置振动若干次，这样来回振动，虽然每次轨迹都不重合，但最终被吸引到相图中的某一点附近运动．混沌运动中奇怪吸引子的存在表明，混沌轨道运动的具体位置虽然局部不稳定，但全局稳定，但轨道的大体位置是在吸引子上．

周期吸引子和拟周期吸引子因其周期性，故功率谱线是分立的(对应尖峰)．白噪声和混沌都是非周期运动，它们的功率谱都是连续的谱．白噪声因其无规则性，其功率谱密度在整个频域内均匀分布，所有频率具有相同能量，所以白噪声具有平坦功率谱．但是混沌运动具有确定系统的随机性，如在倍周期分岔过程中，每一次分岔产生一个新的频率，功率谱中就出现一个对应新频率的峰，当分岔数达到无穷多时，就达到混沌态．尽管混沌系统的连续功率谱仍然有尖峰，但它们会增宽一些．所以混沌的功率谱不是平谱，而具有“噪声背景”和“宽峰”．

4 结语

本文利用MATLAB得到了Lorenz系统、Henon系统和Chen系统的混沌吸引子和功率谱．奇怪吸引子的存在表明混沌轨道运动的具体位置虽然具有对初值的敏感依赖性，但轨道的大体位置是在吸引子上．混沌系统的相轨迹虽然局部不稳定，但全局稳定，相轨迹最终被吸引到相图中的某一点附近运动．混沌的特征是功率谱中出现“噪声背景”和“宽峰”，这个特点反映出了混沌运动具有确定系统的随机性．

［1］ 黄永念．非线性动力学引论［M］．北京:北京大学出版社，2010．1－3．

［2］ 孙红章，赵圆圆，刘钢，等．基于MATLAB复摆振动中非线性行为的仿真研究［J］．商丘师范学院学报，2012，28(6):50－55．

［3］ 孙红章，毛爱霞，苏向英，等．Henon系统动力学行为的MATLAB仿真研究［J］．商丘师范学院学报，2011，27(3):54－57．

［4］ 孙红章，汤正新，刘哲，等．复摆强迫振动中的混沌研究［J］．商丘师范学院学报，2010，26(3):58－60．

［5］ Vadasz P．Analytical prediction of the transition to chaos in Lorenz equations［J］．Applied Mathematics Letters，2010，23(5):503－507．

［6］ Matsuoka C，Hiraide K．Entropy estimation of the Henon attractor［J］．Chaos，Solitons＆ Fractals，2012，45(6):805－809．

［7］ Leonov G A．General existence conditions of homoclinic trajectories in dissipative systems．Lorenz，Shimizu–Morioka，Lu and Chen systems［J］．Physics Letters A，2012，376(45):3045－3050．