一种修正凸组合下降方向的求解单调非线性方程组的算法
2013-12-14廖代喜
王 胜,廖代喜
(湖南工学院数理部,湖南衡阳421002)
非线性方程组的应用非常广泛,在结构分析、大地测量和网络分析等方面都有大量的应用,单调的非线性方程组是其中的一种.若F是单调映射,即F满足
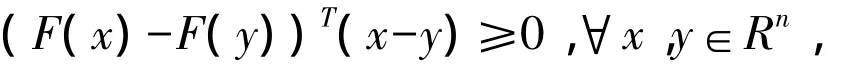
则我们称方程组F(x)=0为单调非线性方程组.
求解单调非线性方程组的方法很多[1-3],共轭梯度法是其中常见的一种,它是由求解优化问题的共轭梯度法变化而来,该算法的下降方向具有充分下降性,并且存储量小,计算上容易实现,收敛速度较快.MPRP算法和CGD算法都是比较好的共轭梯度算法,其区别在于下降方向的不同.
求解单调非线性方程组的MPRP算法[4]中,下降方向为:
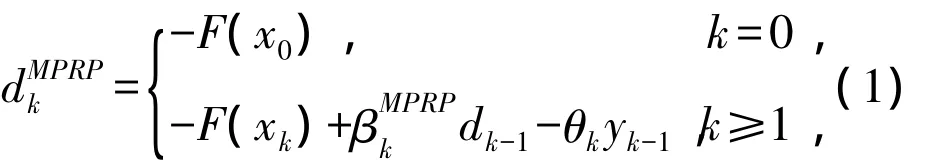

为进一步改进下降性能,可以将这两种算法的下降方向(1)式和(2)式进行凸组合,即给定某一个常数μ∈[0,1],取新的下降方向为:

1 凸组合下降方向的算法
步1 给定初始点x0∈R,取常数σ∈(0,1),ρ∈(0,1),令 k:=0,取精度 ε>0;
步2 如果‖F(xk)‖≤ε,则终止算法,得到方程F(x)=0的解xk,反之由(1)式计算,由(2)式计算,再由(3)式计算下降方向dk;
步3 由线搜索计算步长 tk,tk=max{ ρi:i=0,1,2,…},使之满足
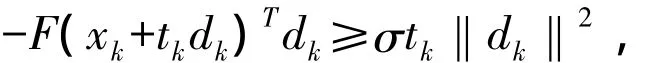
令zk=xk+tkdk;
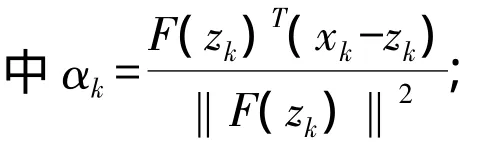
步5 选 取 合 适 的 ξk,令 xk+1=xk-ξkαkF(zk),1≤ξk≤ξ<2,使之满足
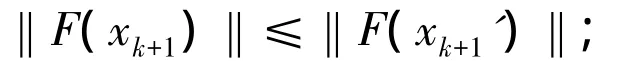
步6 令k:=k+1,转步2.
2 全局收敛性
由文献[6],凸组合下降方向的算法是全局收敛的,通过数值实验,凸组合下降方向的算法优于MPRP算法和CGD算法,下面直接给出收敛性定理.
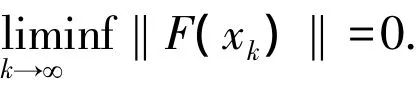
3 修正算法
凸组合下降方向算法的不足之处在于参数μ是固定不变的,按照某一规则动态地选取参数μ会不会具有较好的数值结果,是值得研究的问题,考虑极端的情形,即取μ=1或者μ=0,这实际上是MPRP算法和CGD算法的杂交算法.具体操作如下:

修正算法与凸组合下降方向算法的区别在于参数μ的选取不一样,修正算法的下降方向为:
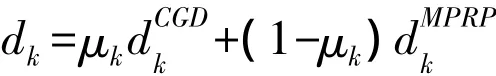
μk的取值由(4)式决定,由于μk仍然属于闭区间[0,1],因此修正算法具有全局收敛性.
4 数值试验
本节我们对修正算法进行数值试验,并将其数值结果与凸组合下降算法的数值结果进行比较.设置精度 ε=10-5,参数 ρ=0.6,σ=0.0001,另外,假如迭代次数达到5000次时还不满足终止条件也终止算法,此时,算法终止于非稳定点.所有的程序在相同条件的平台上运行.
考查单调非线性方程组F(x)=0的求解问题,这里 F(x)=(f1(x),f2(x),…,fn(x))Τ,fi(x)=exi-1,i=1,2,…,n,x∈Rn,初 始 迭 代 点 取 不 同 维 数的(1,1,…,1)Τ,(10,10,…,10)Τ,(-10,-10,…,-10)Τ,(1数值试验的结果如表1:
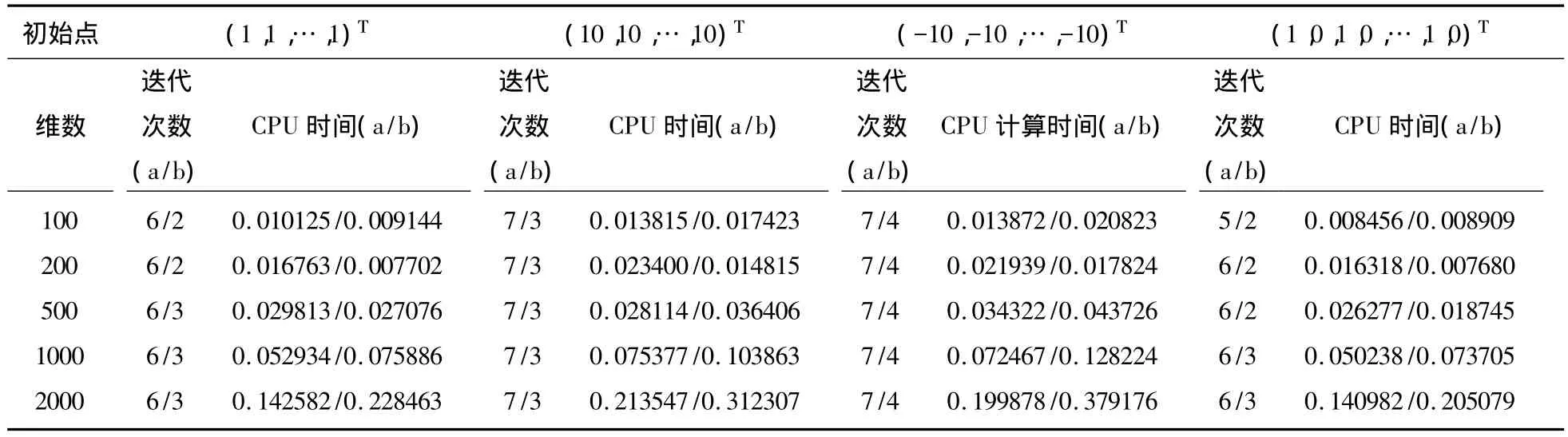
表1 凸组合下降方向算法和修正算法的数值结果Tab.1 The numerical results for convexly combine descent directions algorithm and modified algorithm
5 结论
通过两个算法的数值试验结果,修正算法迭代次数这一指标上明显优于凸组合下降方向算法,但在CPU计算时间上稍逊于原算法,这说明修正算法比凸组合下降方向算法具有更快的下降方向,但由于每次迭代时都需要计算范数,这花费了一定的时间.综合来看,修正算法仍不失于求解单调非线性方程组的一种比较好的算法.
[1]Zhou W J,Li D H.A globally convergent BFGS method for nonlinear monotone equations without any merit functions[J].Mathematics of Computation,2008,77(264):2231-2240.
[2]Yan Q R,Peng X Z,Li D H.A globally convergent derivative-free method for solving large-scale nonlinear monotone equations[J].Journal of Computational and Applied Mathematics,2010,234(3):649-957.
[3]Zhou W J,Li D H.Limited memory BFGS method for nonlinear monotone equations[J].Journal of Computational and Applied Mathematics,2007,25:89-96.
[4]Zhang L,Zhou W J,Li D H.A descent modified Polak-Ribière-Polyak conjugate gredient method and its global convergence[J].IMA Journal of Numerical Analysis,2006,26(4):629-940.
[5]Xiao Y H,Zhu H.A conjugate gradient method to solve convex constrained monotone equations with applications in compressive sensing.Journal of Mathematical Analysis and Applications[EB/OL].http://dx.doi.org/10.1016/j.jmaa,2013-04-17.
[6]王胜,关洪波.求解单调非线性方程组的凸组合算法的收敛性[J].湖南文理学院学报(自然科学版),2013,25(2):21-25.
