均匀连续渗透流场中的“达西悖论”

高宗军

(山东科技大学，山东 青岛266590)

1 达西定律及其推论

1852—1855年间，法国水力学家达西(H.Darcy)在装满砂的圆筒(图 1)中进行了大量的实验［01］，［02］得到如下关系式:

式中 Q为渗流量;H1、H2为通过砂样前后(即上、下游过水断面)的水头;L为砂样沿水流方向的长度(即上下游断面的距离);A为实验圆筒的横截面积，包括砂粒和孔隙二部分面积在内;K为比例系数，称为渗透系数。

图1 达西实验装置

这就是著名的达西定律，又称为线性渗透定律，是指流体在多孔介质中遵循渗透速度与水力梯度(渗透方向上水头损失与渗透途径的比值，无量纲)呈线性关系的运动规律。

达西定律的表达式还有另外一种表达方式［01］，［02］，即

式中，V是渗透速度;K是渗透系数，意义同前;J为水力坡度，是水头差与渗透距离的比值，即J=(H2-H1)/L。以微分的形式，J=dH/dL，此时称为水力梯度。

大量的研究表明，当雷诺(Reynolds)数处于1～10时，地下水运动符合Darcy定律。实际地下水尤其是天然状态下的地下水，其运动速度往往都很缓慢，因此，绝大多数情况下地下水流服从达西定律。

由达西定律可以得出:在均匀连续渗透介质中，地下水的流动都遵循这样的规律，即渗透速度与水力梯度(渗透方向上水头损失与渗透途径的比值，无量纲)呈线性关系;由于均匀连续介质是均质各向同性的，介质的孔隙度及有效孔隙度是处处相等的，因而上述线性关系应该处处遵循，即其比值(斜率)的大小—渗透系数K的值—应该是处处相等的。

如果我们坚信，均质各向同性的渗透介质，其渗透系数K的值和有效孔隙度ne的值在整个流场中处处相等，那么在同样的水头差驱使下，地下水流的渗透速度V应该与渗透途径的长度L具有线性负相关的关系:

即在等水头差时

同样地，由于渗透速度V与实际流速u之间具有线性关系

式中ne为有效孔隙度。则有

或者，在等水头差时同种介质应该有下式成立

然而，通过沙槽的试验，其结果却并非如此，相同的沙充满的砂槽内，上述结论并不成立，即K值是不断变化的，在同样的水头差驱使下，实际流速与运动途径的积并非常数。

2 试验结果

2.1 模拟降水及地势差异情况下的试验结果

梁杏等利用自行设计的地下水流系统演示仪，直观地展现了多级次地下水流系统——局部的、中间的和区域的水流系统［03］，［04］。

根据梁杏等所做的试验证实［03］，沿着局部流动系统边界，地下水由补给区到排泄区的时间约为6.5～32.3 min，沿着中间流动系统的边界，地下水由补给区到排泄区的时间约为110.5 min，而沿着区域流动系统边界，地下水由补给区到排泄区的时间约为260.6 min.

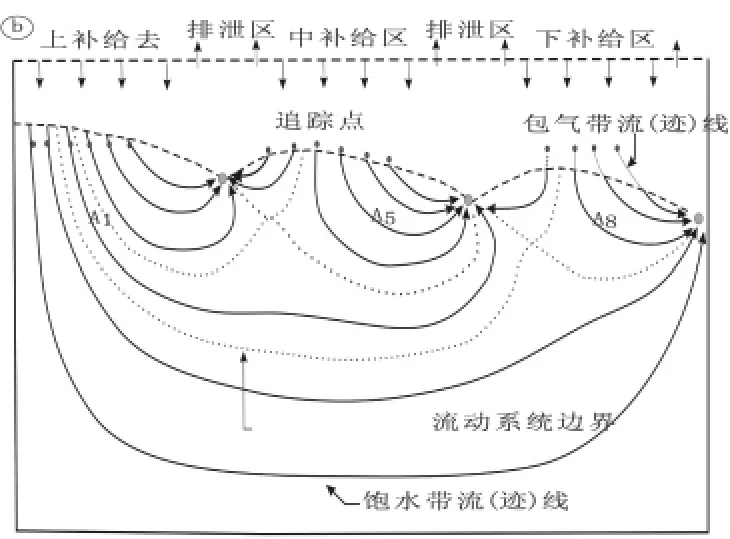
图2 不同降水强度情况下三级地下水流系统模拟试验结果(梁杏，2010)［03］:所观测到的流动系统的阐释

另据梁杏等2008年的内部讲座资料，局部流动系统的边界线交替时间约15 min时，中间流动系统的边界线交替时间约250 min，区域流动系统的边界线交替时间达到665 min，局部与区域的水循环交替时间差可达数十倍至上百倍!

而实际上，由图2我们可以看出，局部流动系统的边界长度大于中间流动系统边界长度的1/2，中间流动系统边界长度也大于区域流动系统边界长度的1/2;但从水交替时间来看，局部系统水流速度远大于中间系统的水流速度的2倍;同样地，中间系统水流速度也远大于区域水流系统的水流速度的2倍。我们根据式(2)，可以由速度及渗透距离求得K值的大小，列于表中(表1)。

显然，只要有效孔隙度大小相等，则所求得的K值的大小是处处不等的!由文献［03］所得结果是:随着渗透距离的增加，其K值是逐渐增加的;相反，由梁杏于2008年所做的讲座，其K值是逐渐递减的。对于这种相反的结果，目前尚不清楚是何原因造成的。

2.2 等水头补给条件下试验结果

作者也设计了类似的砂槽试验。在均质各向同性的渗透介质中，顶部设为定水头自由水体，当具有不同的排泄点时，也出现了具有不同等级的水流系统的图景(图3，图4)

该试验的结果也证实，在不同的流线上的水流速度是大相径庭的。同样根据式(2)及试验结果，求得了在相同水头差(45 cm)情况下的不同流线(迹线)上的水流速度及K值的大小(表2，表3)。

可以看出，K值的变化既有规律性，也有不确定性。其中的原因，除了观测误差、试验用示踪颜色所带来的误差外，可能还有其它的原因，是值得深入思考的问题。

表1 依照实验数据求出的K值在均匀渗流场中的差异性

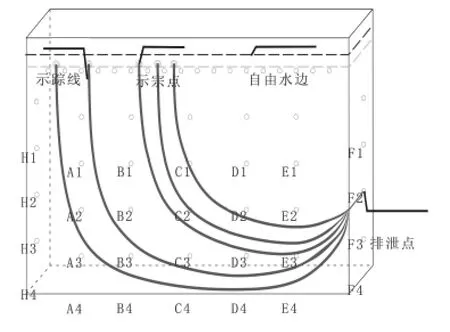
图3 等水头补给及单个排泄点条件下均匀渗流场中流线(迹线)的分布

3 讨论

事实上，托特等［05］，［06］，［07］，［08］，［09］在几十年以来的对地下水流系统的论述中，都提到过地下水流系统具有分级，不同级别的地下水流系统中的水流运行(径流)时间存在很大差异等，Winter等更加形象地描绘出，这种差异在时间上会达到若干数量级(图4)［10］。虽然他们都未涉及达西实验或达西定律的相关内容，但在分析问题的时候，都自觉不自觉地把达西定律作为了处处遵守的规则，而忽略或未知在自然界的渗透流场中存在着的这些差异性。

图4 等水头补给及单个排泄点条件下均匀渗流场中流线(迹线)的分布

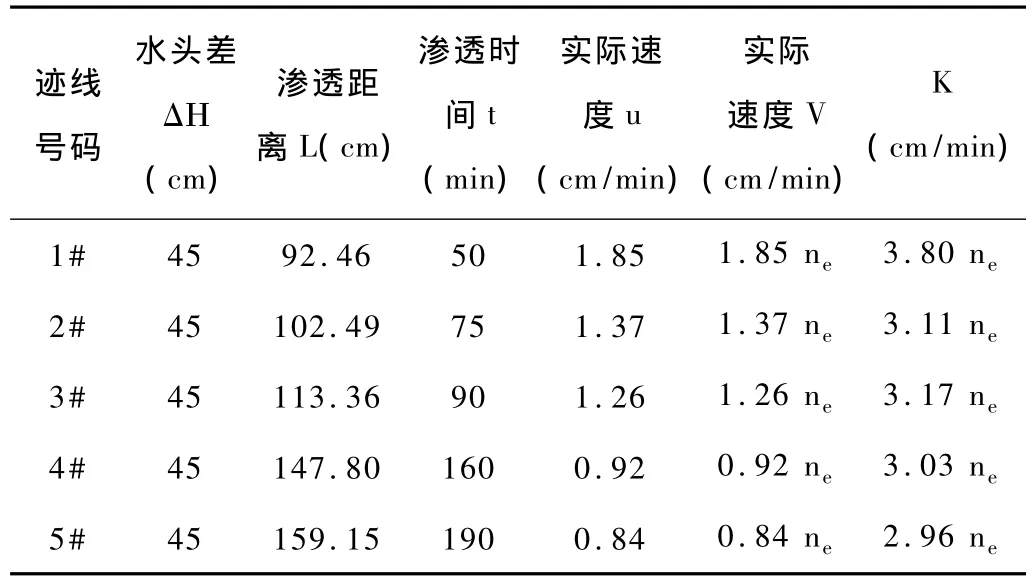
表2 等水头补给条件下均匀渗流场中不同迹线依据达西定律求出的渗透系数

表3 等水头补给条件下均匀渗流场中不同迹线依据达西定律求出的渗透系数

总之，目前人们普遍认为，在均质各向同性介质中，介质的有效孔隙度及地下水的渗透系数应该是处处相等的，且在实际的操作中也是这样应用的。然而在上述均质各向同性的沙槽中，水流运动试验的结果却并非如此，而是出现了“渗透系数”“K值”处处不等的局面，因而此文中称之为“达西悖论”。故此笔者认为，地下水流系统理论与达西定律之间应该存在某种尚不确定的关系，值得深入探讨。

图5 地下水流系统示意图。补给区到排泄区地下水流运行距离、深度及时间(据Winter等，1998)

［1］薛禹群，朱学愚.地下水动力学［M］.地质出版社.北京:1979.7.

［2］薛禹群.地下水动力学［M］.地质出版社.北京:1997.9.

［3］Xing Liang，Yu Liu，Menggui Jin，et al.，2010.Direct observation of complex Tóthian groundwater flow systems in the laboratory.Hydrological Process.24:3568-3573.

［4］张人权，梁杏，等.水文地质学基础［M］.地质出版社.北京:2011.1.

［5］Tóth J.1962.A theoretical analysis of groundwater motion in small drainage basins in central Alberta，Canada.Journal of Geophysical Research 67(11):4375–4387.

［6］Tóth J.1963.A theoretical analysis of groundwater flow in small drainage basins.Journal of Geophysical Research 68(16):4795–4812.

［7］Tóth J.1978.Gravity-induced cross-formation flow of formation fluids，Red Earth Region，Alberta，Canada.Water Resources Research 14(5):805–843.

［8］Tóth J.1999.Groundwater as a geologic agent:an overview of the causes，processes and manifestations.Hydrogeology Journal 7(1):1–14.

［9］Tóth J.2009.Gravitational Systems of Groundwater Flow:Theory，Evaluation and Utilization，Cambridge University Press:Cambridge.

［10］T.C.Winter，J.W.Harvey，O.L.Franke，and W.M.Alley.Ground Water and Surface Water A Single Resource.USGS Circular 1139，1998.