用MATLAB PDE工具箱解地下水稳定流问题
2013-12-14余震果
张 敏,余震果
(辽宁师范大学数学学院,辽宁 大连116029)
有限元法是解决地下水问题的主流方法,利用此方法求解问题需选定单元的形状;对求解域作剖分;对节点编号;构造基函数;形成有限元方程;求解方程。有些实际问题求解区域比较复杂,在对几何区域进行单元网格剖分、节点编号时比较繁琐,直接编写程序具有一定的难度。偏微分方程(PDE)工具箱提供了研究和求解空间二维偏微分方程问题的一个强大而又简单便捷、灵活实用的环境。利用PDE工具箱求解偏微分方程问题有两种方法,一种是直接使用图形用户界面(GUⅠ),可以从繁杂的编程中解脱出来,很容易实现复杂的几何区域剖分、直接加密网格,也可以进行复杂的定解条件下的偏微分方程求解,直接生产M代码。另一种是采用命令函数编写程序计算。应用GUⅠ解决地下水问题步骤为:1.区域选择;2.模型建立;3.定义边界;4定义PDE类型和系数;5.三角形网格剖分;6.求解PDE;7.解的图形表达;8.数据输出。本文将利用MATLAB PDE工具箱的基本原理及步骤解决承压和非承压的稳定流问题,只具体应用了GUⅠ没有应用命令行编辑去解决问题。
1 承压含水层定降深完整井稳定流计算
如图1[1],一承压含水层完整井,含水层为均质等向,厚度M,渗透系数K,含水层中的原始水位H0,抽水稳定后,测得井中水位hw,滤水管半径rw,抽水井的影响半径R。取 K=0.8 m/d;M=100 m;R=300 m;H0=170 m;rw=80 m;hw=120 m。
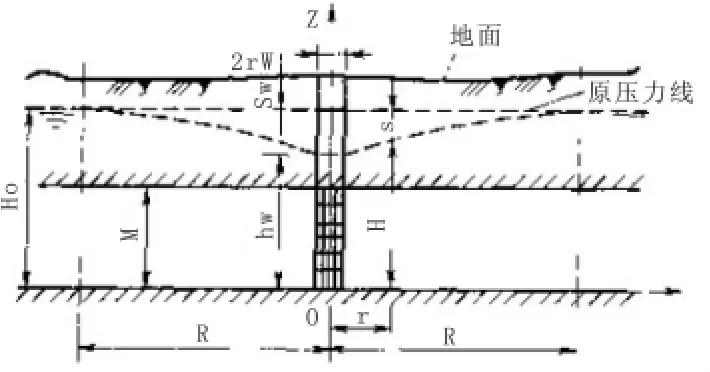
图1
此方程属于椭圆型方程,它的基本形式为:-▽(c▽u)+au=f,inΩ。其中Ω是平面有界区域。对应此题c=KM,a=0,f=0。Ω 为环形,边界为 Dirichlet条件(hu=r),在边界x2+y2=R2上时,h=1,r=170,在边界 x2+y2=上时,h=1,r=120。
应用PDE工具箱来解决这个问题的具体步骤:
1)在MATLAB命令窗口输入 pdetool并运行,出现 PDE图形用户界面(GUⅠ)。
2)在GUⅠ中对区域进行选择,此题区域为环形,分步完成几何区域C1、C2。用菜单或快捷工具画出矩形 C1、C2,然后再Set formula栏直接键入C1-C2。
3)定义边界条件,可单击Boundary菜单中Specify Boundary Conditions选项或直接单击Ω,打开Boundary Conditions对话框,输入边界条件,此题全部设为Dirichlet条件,边界颜色都为红色。
4)定义PDE类型和PDE系数,选择PDE菜单中的PDE Mode命令,进入偏微分方程模式,再单击PDE Specification选项,设置方程为椭圆型,在type of PDE中选择Elliptic,再分别输入参数 c,a,f,c=160,a=0,f=0。
5)对区域进行三角形网格剖分,可用initmesh和refinemesh进行剖分,还可以选择Mesh菜单中的Ⅰnitialize Mesh命令进行剖分、Refine Mesh命令对网格加密。
6)选择Solve菜单中Solve PDE命令,或直接单击“=”求解偏微分方程且显示图形解。
7)解的图形表达,单击Plot菜单中的Parameters选项,打开Plot Selection对话框,选中相应的选项,然后单击 Plot,显示三维图形解。
此类地下水问题,对网格进行剖分,直接编写原始程序都较复杂。利用PDE工具箱对区域进行网格剖分直观简捷。本题对区域进行6次初始化网格剖分,使解的精度得以提高。图2为承压含水层定降深完整井的降水漏斗曲面图。
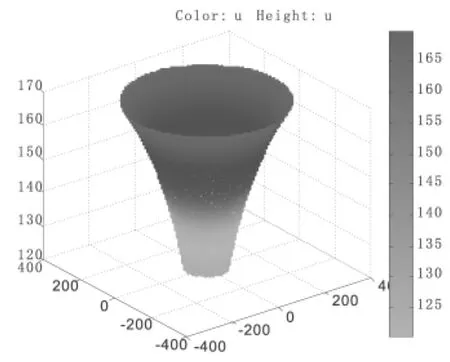
图2
2 非承压含水层稳定流计算
如图3[1]所示是一平面矩形河间地区,河口冲积扇平面中设置的灌,排河渠网的一典型地块,由于主河渠水位均较高,所以造成河渠间的地下水水位过高,这一高位地下水长期侵渍,使土地盐化,碱化。为了排盐排碱,进行耕种,在垂直于河渠方向没隔间距挖一条深排水沟进行排油,以降低地下水位。
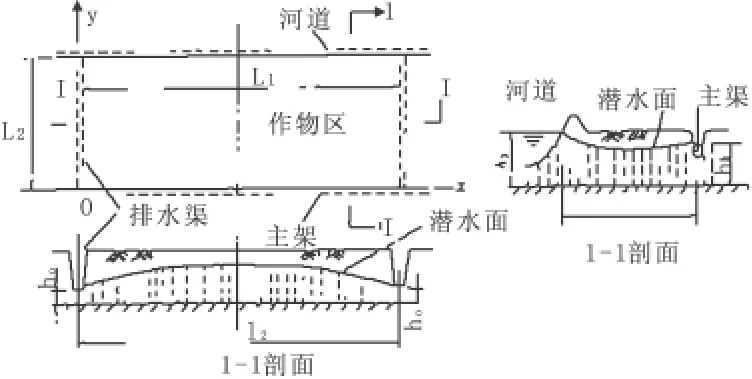
图3
此方程为非线性椭圆型方程,此类方程的基本形式为-▽(c(u)▽u)+a(u)u=f(u),inΩ 。其中 c,a,f可以是解 u的函数。对应此题c=Kh,a=0,f=0。Ω为矩形区域,边界条件为Dirichlet条件(hu=r),h和r是定义在αΩ上的函数,对于非线性情形,h和r可以依赖于u。渗透系数为K;已知水头为h0;主渠内水位为h1;主河内水位为h2。分别取K=-0.8 m/d;h0=10 m;h1=30 m;h2=40 m;l1=250 m;l2=120 m。
求解步骤与上例有一点区别,即对上例所述第六步进行设置,选择 Solve菜单中 Parameters的 Use nonlinear solver,如图4。其余大致相同。图5是利用PDE工具箱对上面二维稳定流问题做出的水头函数图形。
3 结语
本文是直接利用GUⅠ解决地下水计算问题,应用此种方法简单便捷。除了用GUⅠ解决还可以用工具箱中的命令来创建描述几何图形的M文件来解决问题。有时会遇到利用GUⅠ无法解决的问题,例如几何图形不是由直线、圆弧、椭圆弧及其组合而成的图形时,就只能用工具箱中的命令函数编写程序计算,此法比直接编写原始程序简单快速。
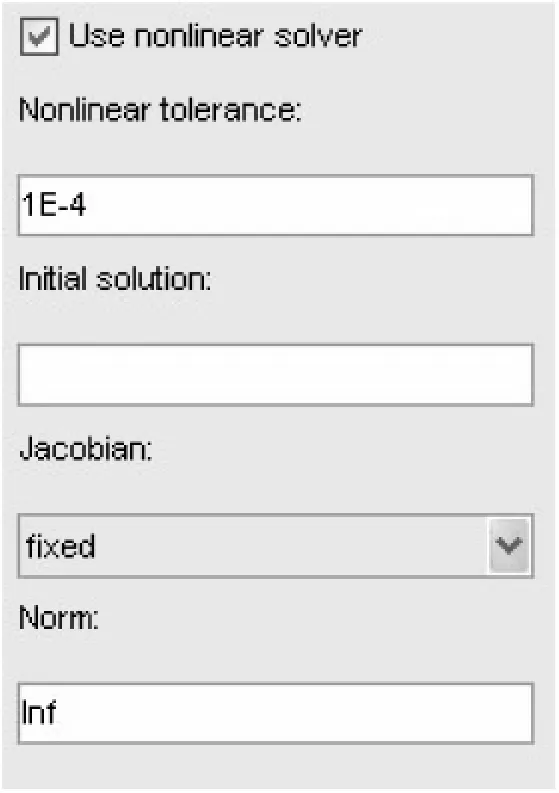
图4
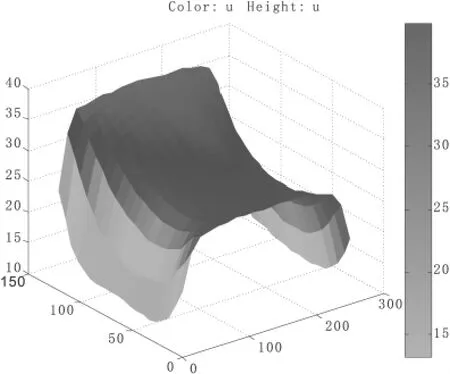
图5
[1]王君连.工程地下水计算[M].北京:中国水利水电出版社.2004.
[2]薛禹群,叶淑君,谢春红,张云.多尺度有限元在地下水模拟中的应用[J].水力学报.2004(7).
[3]陆君安,尚涛,谢进,等.偏微分方程的 MATLAB解法[M].武汉:武汉大学出版社.2001.
[4]陆金甫,关治.偏微分方程的数值解法[M].北京:清华大学出版社.2004.
[5]苏金明,张莲花,刘波.MATLAB工具箱应用[M].北京:电子工业出版社.2004.
[6]陈群,谢家烨.PDETOOL工具箱在磁共振技术中的应用[J].江西科学.2009,27(2).
[7]李明.偏微分方程的 MATLAB 解法[J].湖南农机.2010,37(3):89—91.
