策克白垩纪承压水含水层渗透系数变化规律

商玮麟，马文学，庞家伟

(1.3.中国地质大学环境学院，湖北 武汉430074;2.内蒙古自治区第一水文地质工程地质勘查院，内蒙古呼和浩特010020)

1 区域概况

1.1 区域地质条件概述

研究区域位于银—额盆地范围内石板井一小黄山缝合带以北的额济纳旗区的居东凹陷，与北山北带相毗邻，其白垩纪沉积(此次研究的承压水含水层为白垩纪沉积)作用主要受居东1号、居东2号断层控制。该凹陷位于居延海凹陷的东北部，是一个东北断东南超的中新生代单断凹陷，面积为2 570 km，凹陷的基底最大埋深6 350 m。凹陷的沉积盖层由侏罗纪、下白垩纪和新生界沉积物组成.中生界缺失三叠纪和上白垩纪，侏罗纪和下白垩纪的顶底面均为区域不整合面。居东1号断裂最显著的特点是侏罗纪、早白垩纪沉积中心迁移作用明显，它在侏罗纪以前已经形成，印支运动晚期活动剧烈，下降盘沉积了大套近千米的侏罗纪沉积物，侏罗纪末期构造回返，居东2号断裂反转成为逆断层，侏罗纪沉积物自南向北逆冲，出露水面，遭受剥蚀，剥蚀量近千米;早白垩纪早期居东1号断裂再次恢复正断层性质，断层下降盘边沉降边沉积，堆积了800～900 m的早白垩纪沉积，此时的居东2号断裂已取代居东1号断裂在凹陷北部迅速发展，演变成凹陷主控断裂，致使下白垩纪沉积、沉降中心向西北方向迁移。目前在凹陷内发现的构造大多数为断背斜，主要发育于居东2号断裂的下降盘，形成了准扎海断背斜带(侏罗纪)和淮北断背斜带(下白垩纪)，这些构造大多数形成于燕山期。本文主要研究区域白垩纪承压水含水层的水化学特征分析和研究。

研究区承压水含水层主要为扇中亚相即水下扇的主体部分，由扇中辫状水道及水道间微相组成。扇中辫状水道微相主要岩性为砾岩、含砾砂岩、中细粒砂岩及少量的泥质岩、砂岩中常见泥砾，底部常见冲刷面，层理构造可见粒序层理、块状层理、交错层理，常由多个粒度大致向上变细的砂砾岩叠加形成叠合砂体。大型板状交错扇中水道间微相岩性主要为粉砂质泥岩、泥页岩夹薄层泥质粉砂岩、细砂岩，以水平层理为主，含介形虫、叶肢介及植物碎片等化石。

1.2 区域水文地质条件概述

研究区地貌上表现为向南倾斜的戈壁地形和强烈剥蚀的准平原地形，是蒙古人民共和国境内戈壁阿尔泰山东端山前倾斜平原的南延部分(见图1)。地形起伏不大，大约以5‰的坡降向南倾斜。区内洪流沟谷发育，切割密度大，除少数沟谷中生长有一些耐旱植物，广大戈壁平原上无植物生长。

区内气候干旱，年降水量小(多年平均年降水量为32.80 mm)，加之泥岩与砂砾岩互层结构，透水性较差，所以大气降水所形成的洪流对地下水补给量比较小，特别是对层间承压水的补给，更是少之又少。该区内潜水基本没有，局部冲沟中含少量的水。主要是白垩系地层中的碎屑岩类承压水。在构造上，表现为碎屑岩建造的单斜“盆地”，自北向南倾斜。由白垩系泥岩和泥质砂砾岩组成(见图2)，表层覆盖有一层厚度不大的洪积砾砂层。因受基底局部隆起作用的影响，有些地区的碎屑岩被顶托起抬升，外貌呈龙岗状裸露地表。“盆地”北缘耸立着山势高峻的戈壁阿尔泰山，海拔在2 000 m以上，降雨量相对较大，所以在山前断裂带有泉群出露，沿山前呈东西条带状展布(见图2)。工作区位于泉群下游，接受戈壁阿尔泰山基岩裂隙水侧向补给。随着径流途径增长及运动速度减缓，水质有逐渐变差的趋势。承压水排泄于额济纳冲-湖积平原和嘎顺淖尔冲湖积平原而补给平原区地下水。

图1 区域水文简略图

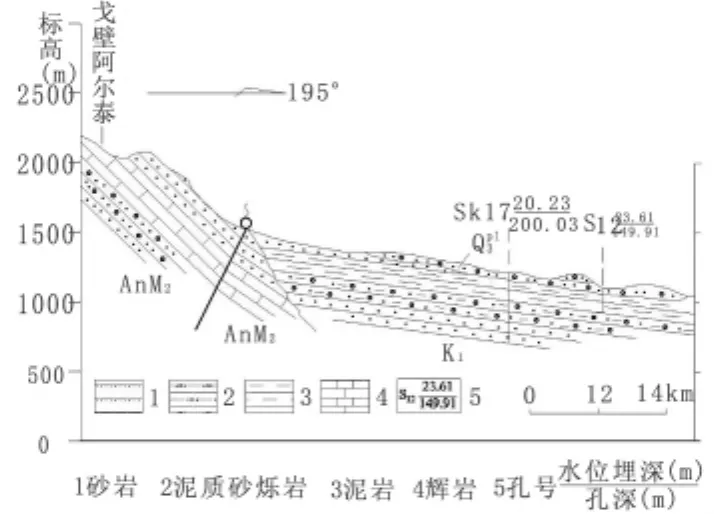
图2 钻孔SK17到戈壁阿尔泰水文地质示意剖面图

2 观测数据分析

对从区域52个取样点获得的渗透系数值进行分析。首先将渗透系数单位由m/min转换为m/d。通过自然对数转换含水层的渗透系数后，可得到较好的空间变异结构［1］，故取对数后(ln K)进行分析。表1为该含水层渗透系数观测值基本统计结果。统计结果显示，渗透系数的范围在3.51 m/d至0.62 m/d之间，偏态为正偏;取对数后范围在1.26 ln(m/d)至-1.7 ln(m/d)之间，平均值约为0.25 ln(m/d)，差异不大，且偏态为负偏。将转换前、后的渗透系数进行卡-方检定(Chi-square test)［2］，并由组数及参数的个数计算、检验正态分布优度，经计算后可知取自然对数后的渗透系数自由度为4，其统计值为 2.532(见表2)，在5%显著水平［3］下其理论卡方检定值为6.070 5，由此可知该含水层的渗透系数呈对数正态分布，不满足正态分布。［4］

表1 研究区白垩纪承压水含水层渗透系数(m/d)描述性统计结果

表2 研究区白垩纪承压水含水层渗透系数观测值卡方检验正态分布优度

3 空间变异结构分析

3.1 实验变差函数

变差函数是地质统计学的基本工具，它可以把样本空间上的区域变量相互联系起来。本文中采用尺度估计法求得实验变差函数2Y*(h)=3 558{med|Z(xi)-Z(xi+h)|}2这一估计量是非常稳定的，对严格的正态的数据只有约35%的渐进效率，但是，地质统计学的绝大多数实际应用可以证明这种方法是非常有效的。根据关系式:R(x)=Z(x)-m(x)确定变差函数。根据各个点的剩余值，分别用非列线不等距变差函数计算了0度和90度方向的实验变差函数(见图3、图4)。［5］

3.2 理论变差函数

根据已经获取的稳健变差函数的变化趋势拟合一个理论模型，即理论变差函数。

球状模型:

式中:C0为块金常数;C0+C为基台值;C为拱高;a为变程。本文在推求理论变差函数时目估有基台值变差函数的趋势［6］因而采用了球状模型，如上式所述。在0度方向求得结果:C0=0，C=0.127，a=10 100;在90度方向求得结果 C0=0，C=0.982，a=14 900。［7］

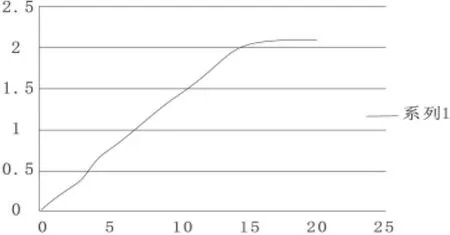
图3 90度方向的实验变差函数

3.3 变差函数的确认

在进行克里金插值推估前，需先对前文选定的理论变差函数模型进行验证。检验原始变差函数模型使用克里金交互验证(Cross-Validation)所产生的残差值(Reduced Residuals)(原始数据减去插值)的概率密度函数是否满足标准正态分布，即克里金平均误差(Kriging Average Error;KAE)是否接近零，克里金均方误差(Kriging Reduced Mean Square Error;KRMSE)是否接近1［5］若方差大于1，表示实际方差比估计方差大，需将变差函数的基台值调高做校正;反之，需将基台值调低，重新验证残差值的统计分布是否接近标准正态。克里金交互验证的最终结果 KAE值为0.126，KRMSE值为1.273，皆在允许误差范围之内。［8］

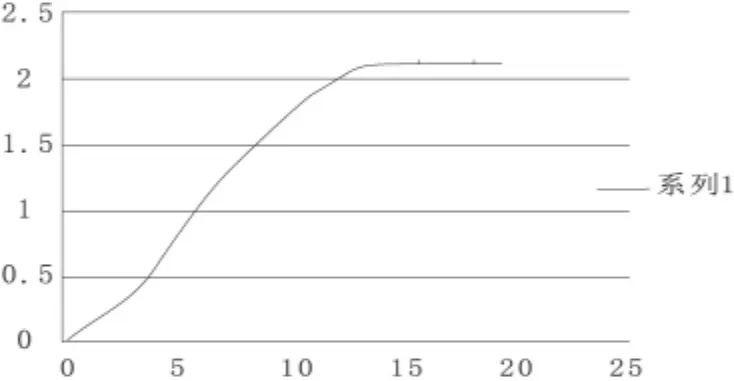
图4 0度方向的实验变差函数

3.4 Kriging插值

经交叉验证检定理论变差模型的可行性后，在研究区域内采用sufer程序以258行261列的格网对白垩纪承压含水层渗透系数的对数进行二维的普通克里金插值，绘制成渗透系数等值线图，结果如图5所示。［9］

图5 策克地区对数渗透系数等值线图

3.5 研究区对数渗透系数场区域性分析

在研究区西部的一区(见图6)，而西部边缘地带大地纵坐标4 711 000到4 714 000之间无钻孔，此处绘图结果为插值所得，该区域白垩系含水层对数渗透系数分布以(1 766 000，47 126 000)为峰值点，向四周呈放射状递减，根据钻孔剖面(见图7)及岩土样分析，沉积地层中扇中辫状水道及水道间微相均较薄，前者厚6～11 m，后者厚8～13 m，表明此处水交替频繁，而岩土样分析结果显示颗粒平均粒径由峰值点向四周放射状递减，而分选程度由峰值点向四周变得越来越好，因此此处白垩纪早期极有可能为小型河流入湖口，这就解释了对数渗透系数的变化情况。二区由西向东白垩纪早期水下扇沉积越来越深入古湖泊内部，渗透系数也越来越小。

图6 研究区对数渗透系数场解释图

在研究区中偏东的三区，渗透系数由北向南递减，在北部呈山峰形分布南部成呈凹地形分布。根据钻孔剖面(见图8)及岩土样分析，含水层主体自北向南倾斜且逐渐变薄，颗粒平均粒径由北向南递减，而分选程度由北向南变得越来越好，此处白垩纪水下扇沉积由北向南深入古湖泊内部，北部山峰形分布区为古地形凸起处，南部成呈凹地形分布区为古地形下凹处，而中部的渗透系数急剧变化带为两种地形的交界带，可见三区的对数渗透系数场受到地形因素严格控制。

4 结语

本文的空间结构分析结果表明，策克地区白垩纪承压含水层的渗透系数经过自然对数变换后，表现为正态分布，在平稳区域化变量假设条件下具有显著的各向异性。在90°方向具有较剧烈的变化，而在正交的0°方向变化较为平缓。

图7 C-C’地质剖面图

图8 A-A’地质剖面图

研究区对数渗透系数场的分布情况主要受沉积物颗粒粒径和分选程度的控制，而沉积物颗粒粒径和分选程度主要受古地形、地貌、地理控制，这两者影响着区域富水性和水化学特征。

［1］Ouellon T，Lefebvre R，Marcotte D，et al.Hydraulic conductivity heterogeneity of alocal deltaic aquifer system from the kriged 3D distribution of hydrofacies from borehole logs ，Valcartier，Canada［J］.Journal of Hydrology，2008，351:71-86.

［2］王家华，高海余，周叶.克里金地质绘图技术:计算机的模型和算法［M］.北京:石油工业出版社.1999.

［3］Kitanidis P K.Ⅰntroduction to Geostatistics:Applications to Hydrogeology［M］.Cambridge:Cambridge University Press，1997.

［4］Delhomme，J.P.，Spatial variability and uncertainty in groundwater flow parameters:a geostatical approach，Water Resource Research，1979，5(2):269～280.

［5］朝伦巴根，刘廷玺地质统计学及其应用［M］.呼和浩特:内蒙古农业大学出版社.1996.9.

［6］朝伦巴根，和泰含水层渗透系数K的空间变异性研究［J］.地质学报.1994(4):358-367.

［7］张仁铎.空间变异理论及应用［M］.北京:科学出版社.2004.

［8］侯景儒，尹镇南，李维明等.实用地质统计学［M］.北京:地质出版社.1998.

［9］王亮，朝伦巴根 基于非列线数据的泛克立格法在地下水位空间变异性研究中的应用［J］.水资源与水工程学报.2007，18(4):52-54.