一种新型多芯-双模-大模场面积光纤的设计和分析*

郑斯文 林桢 任国斌 简水生

1)(北京交通大学,全光网络与现代通信网教育部重点实验室,北京 100044)

2)(北京交通大学光波技术研究所,北京 100044)

(2012年7月23日收到;2012年8月17日收到修改稿)

1 引言

光纤传输日益增长的需求使得超高容量系统的传输容量已高达100 Tbit/s[1−3].为了克服光纤通信系统的容量限制,多芯光纤(MCF)被用于更高功率的光纤放大器、激光器以及高速大容量光纤传输中,有望成为下一代传输系统的光纤.根据多芯光纤的使用目的,我们将其大体分为两类:低串扰型多芯光纤[4−6]和大模场面积多芯光纤(LMAMCF)[7−9].低串扰型多芯光纤大多用于空分复用系统中[10].多芯光纤大多处于多模状态,高阶模会增大光纤的传输损耗,而大模场面积光纤要求传输损耗较小.目前针对大模场面积多芯光纤的研究还很少.

光纤中的非线性效应是造成光纤容限的根本原因.单模光纤中的非线性系数与有效面积成反比,因此降低非线性效应简单有效的方式就是增加纤芯直径从而增大有效面积.但它的缺点是会增大光纤的微弯损耗及色散.目前制造大模场光纤的方法有:低数值孔径的单模光纤、光子晶体光纤及布拉格光纤等,还有就是采用单模运转下的少模光纤(FMF)来增加纤芯直径而不改变损耗及色散特性[11].然而少模光纤存在一些缺点:模式数目的增加导致传输损耗增大,以及稳定性方面的隐患等.因此,减少少模光纤中的高阶模数目从而减小传输损耗,在大有效面积、长距离传输方面将是亟待解决的问题.

本文针对多芯光纤分类中的第二种,即大模场面积多芯光纤,提出了一种基于多芯结构的双模大模场新型光纤结构.通过合理设计光纤的各结构参量,多芯光纤可以在减少二阶模数目的同时,实现大模场面积传输.这种大模场多芯光纤有望成为下一代高速大容量光纤通信系统用光纤.

2 多芯-双模-大模场面积光纤的结构设计

传统多芯光纤大多采用纤芯呈三角格子排列,本文提出的多芯-双模-大模场面积光纤(MCDM-LMAF)横截面结构如图1所示.在传统多芯光纤上增加两个空气孔,如图中灰色所示,假设空气孔直径与纤芯直径相等,外包层为纯石英结构.表征MC-DM-LMAF特性的结构参量有:假定石英包层的直径为dclad=125µm,折射率为nclad=1.444,纤芯与包层的折射率差∆=ncore−nclad,其中,ncore为纤芯折射率,Λ为芯间距,d为纤芯及空气孔直径,这里定义参数相对孔径大小 f=d/Λ.

图1 双空气孔MC-DM-LMAF光纤横截面结构示意图

3 模场分布特性

由于有限元法不受计算区域内材料属性和几何形状的束缚,具有很强的通用性,并且建模简单,计算速度快,故本文采用全矢量有限元法分析MC-FM-LMAF的模式特性.

在MC-DM-LMAF中,传输各模式的磁场强度H满足亥姆霍兹方程:

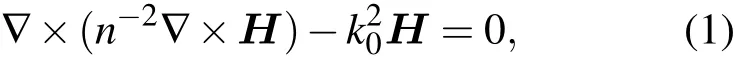
其中,H=H(x,y)exp(−jβz),n为光纤横截面的折射率分布,k0是真空中的波数,β为模式的传播常数.应用有限元法可求出(1)式的特征向量和特征值,即各模式磁场强度H 和传播常数β.给定MC-DM-LMAF的结构参量:纤芯与包层的折射率差∆,芯间距Λ,相对孔径大小 f=d/Λ,就能惟一确定MC-DM-LMAF的折射率分布,从而就能确定波长λ处各模式的磁场强度H和传播常数β.

为了研究MC-DM-LMAF的模场分布特性,首先假设纤芯与包层的折射率差∆=0.3%,芯间距Λ=9µm,相对孔径大小 f=0.4,波长λ=1550 nm,数值计算MC-DM-LMAF各模式的模场分布、有效折射率neff及基模有效面积Aeff.为了进行对比,同样计算了相同结构参量的19芯无空气孔结构的模场分布及有效折射率neff,即图1中的两空气孔替换为与其余17个纤芯相同的纤芯结构,暂且称这种结构为19芯大模场面积光纤.

光纤中导模的模式折射率neff需满足:nclad＜neff＜ncore,折射率低于nclad的模式不能在光纤中传导,由此可以判断其截止特性.经计算,在未引入空气孔时,19芯大模场面积光纤的导模共包括6个模式,即两个简并的基模:HE11-x,HE11-y,四个简并的二阶模:TE01,TM01和两个HE21模.图2给出了这6个模式的模场分布和二维电矢量分布,其中基模有效折射率neff1=1.444341,二阶模有效折射率neff2=1.444124.

图2 19芯结构6个模式的模场分布和二维电矢量分布 (a),(b)基模HE11模的两个简并模式;(c),(d)HE21模;(e)TE01模;(f)TM01模

将19芯光纤最外层两个纤芯替换为空气孔,可以达到减少高阶模数目的目的.由于二阶模的TE01,TM01模的二维电矢量分布是圆对称结构,通过增加两个空气孔,相当于在纤芯外侧形成了一个高阶模泄漏通道,打破了模式的圆对称性,增加了高阶模的泄漏损耗,从而达到了减少模式数目的目的.研究发现,二阶模中的TE01,TM01模截止,光纤中传输的模式只剩下两个简并基模HE11模和两个简并二阶模HE21模,因此这里定义这种光纤为严格意义上的双模光纤.值得注意的是,这里的双模与普通光纤的双模意义不同,普通光纤的双模共包含有六个矢量模,即两个简并的基模HE11模,四个简并的二阶模:TE01,TM01和两个HE21模,也就是两个标量模LP01和LP11模.以下文中的双模光纤均为严格意义上的双模光纤,即传输模式只有两个简并的基模HE11模和两个简并的二阶模HE21模.

图3为双空气孔MC-DM-LMAF中4个模式的模场分布和二维电矢量分布.基模HE11模neff1=1.444297,两个简并模式的有效折射率差双折射数值很小,可以忽略不计.二阶模HE21模neff2=1.444122,两简并模式的双折射1.73×10−7,同样很小忽略不计.计算得二阶模TE01,TM01模neff3=1.44398＜nclad,说明TE01,TM01模被有效地截止,光纤中的传输模式减少为4个.

光纤中基模模场分布属于近高斯型分布,其模场面积为

其中,E(x,y)为基模电场分布.计算得基模有效面积约为1044µm2,远远大于文献[8]中基模有效面积的理论值470µm2.

为了研究双模和单模光纤的带宽,考虑其有效折射率neff随波长λ的变化,如图4(a)所示.可见,其双模运转范围为1500—1930 nm,带宽约为430 nm,其单模运转范围为1930—2800 nm,带宽约为870 nm.改变其结构参量,双模和单模运转波长及带宽也会随之变化.图4(b)为单模、双模运转范围随芯间距Λ的变化情况.可见,随着Λ的增大,双模和单模运转波长逐渐增加,其带宽也随之增大.

图3 双空气孔MC-DM-LMAF 4个模式的模场分布和二维电矢量分布 (a),(b)基模HE11模的两个简并模式;(c),(d)HE21模

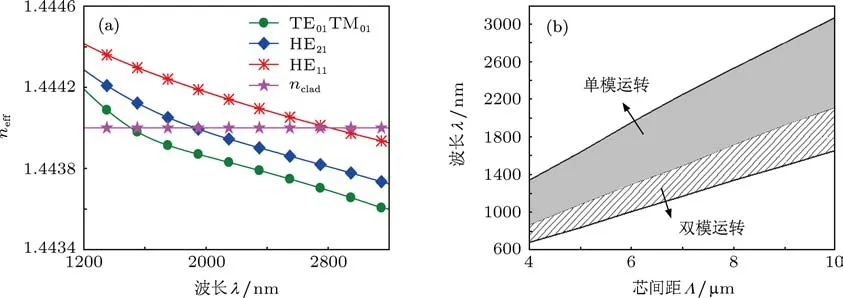
图4 有效折射率n eff随波长λ的变化及单模、双模运转范围 (a)有效折射率n eff随波长λ的变化;(b)单模、双模运转范围随芯间距Λ的变化

4 结构参数对光纤特性的影响

用来表征MC-DM-LMAF的结构参量有三个:纤芯与包层的折射率差∆,芯间距Λ,相对孔径大小f=d/Λ.下面分别研究各参量对MC-DM-LMAF的有效折射率neff及基模有效面积Aeff的影响.

首先假设纤芯与包层的折射率差∆=0.3%,固定相对孔径大小 f=0.2,0.3,0.4,0.6,0.8,1.0,研究芯间距Λ对MC-DM-LMAF有效折射率neff的影响.计算了有效折射率neff随Λ的变化关系,如图5所示.可见,在相同 f时模式neff随Λ的增加而增大,在相同Λ时neff随 f的增加而增大.在相同f和Λ下,基模neff大于二阶模neff,而二阶模HE21模的neff大于二阶模TE01,TM01模的neff.这与19芯无空气孔的结构不同,说明合理设计Λ及 f等参量,可使得TE01,TM01模截止,实现双模传输,减少了二阶模数目.随着Λ的进一步减小,HE21模甚至也可以截止,实现单模传输.图中不同的 f对应的TE01,TM01模截止时的Λ大小并不相同,这说明为了减少二阶模数目,不同的结构参量存在最佳的组合值.不同的 f对应的单模、双模传输的Λ值如表1所示.可见随着 f的增大,Λ值变小.这是由于随着 f,Λ的增大neff会增大,为了使得TE01,TM01模截止,必须使其neff小于包层折射率,因此在增大 f时需减小Λ的值,以保证TE01,TM01模的neff始终小于包层折射率.

图5 双空气孔MC-DM-LMAF有效折射率n eff随芯间距Λ的变化曲线 (a)—(f)分别表示相对孔径大小 f=0.2,0.3,0.4,0.6,0.8,1.0时有效折射率n eff随芯间距Λ的变化关系

表1 不同相对孔径大小 f对应的最佳芯间距Λ值

为了研究双空气孔MC-DM-LMAF各结构参量对基模有效面积的影响,计算了双模传输时不同f下基模有效面积Aeff随芯间距Λ的变化曲线,如图6所示.图中不同 f下基模Aeff随着Λ的增加先缓慢下降然后上升,下降部分是由于随着Λ减小基模接近截止,因而Aeff增大.当基模远离截止时,随着Λ增加Aeff增大,且 f越小Aeff越大.这是由于随着Λ增加,纤芯的等效尺寸增大,从而Aeff增大.f越小,说明每个纤芯的尺寸越小,整个纤芯的等效折射率越小,光功率更多地分布于包层中,使得Aeff增大.从图6中可以看出,当 f=0.2,Λ=17.2µm时,Aeff最大,约为3512µm2.

下面研究纤芯与包层折射率差∆对光纤有效折射率neff及基模有效面积Aeff的影响.固定相对孔径大小 f和芯间距Λ,计算了三组不同 f和Λ下,neff随∆的变化曲线,如图7所示.可见,随着∆的增加neff逐渐增加,并且在相同∆下,说明合理设计∆也能达到双模或者单模传输.在不同 f,Λ下,TE01,TM01模截止时的∆并不相同,如表2所示.可见随着 f,Λ的增加∆变小.这是由于随着 f,Λ或∆增加neff会增大.为了使得在增大 f,Λ时需减小∆,以保证TE01,TM01模的neff始终小于包层折射率.

图6 不同相对孔径大小 f下基模有效面积A eff随芯间距Λ的变化曲线

图7 MC-DM-LMAF有效折射率n eff随纤芯与包层的折射率差∆的变化曲线 (a)f=0.4,Λ=9µm;(b)f=0.4,Λ=10µm;(c)f=0.6,Λ=9µm

表2 不同 f,Λ对应的最佳∆值

图8分析了光纤中基模有效面积Aeff在不同f和Λ下随折射率差∆的变化关系.可见,随着∆的增加Aeff减小.这与传统光纤是类似的,即∆越大,纤芯折射率就越大,使得光功率较多的分布于纤芯中,因而Aeff越小.基模有效面积最高约为2700µm2.这里只给出了三种 f,Λ的情况,通过合理设计 f,Λ及∆的值,基模Aeff可以达到更高,满足大容量、高功率传输等实际应用的需求.

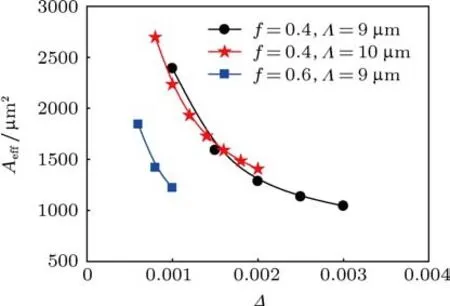
图8 不同 f和Λ下基模有效面积A eff随折射率差∆的变化曲线

5 基模弯曲损耗特性分析

当光纤发生弯曲时,光纤形变导致的光纤几何结构及折射率差∆的改变,使其传输特性受到影响.假设光纤沿+x方向弯曲,其横截面等效折射率分布可以表示为[12]

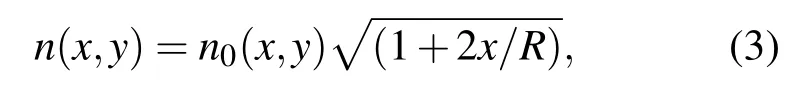
其中,n0(x,y)为光纤初始折射率分布,R为光纤弯曲半径.

当光纤外层涂以低折射率涂覆层时,常用的涂覆为低折射率环氧树脂,其折射率为1.36,计算得其弯曲损耗非常小,可以忽略不计.说明这种光纤在实际制作中可以涂低折涂覆,以实现大有效面积的同时减小弯曲损耗.当光纤外层为高折射率涂覆时,常用的是紫外固化聚合物材料,其折射率为1.5,计算了不同弯曲半径下基模弯曲损耗及模场面积的变化关系,如图9所示.其中FM-x,FM-y分别代表基模的两个偏振态.可以看出,随着弯曲半径的增大,弯曲损耗及模场面积呈指数单调递减.基模两个偏振态在弯曲半径R小于0.2 m时,其弯曲损耗不同.当R为0.14 m时,FM-x的弯曲损耗约为54 dB/m,基模Aeff约为1337µm2,而FM-y的弯曲损耗约为10 dB/m,基模Aeff约为1450µm2,这是由于在x轴方向引入双空气孔的缘故.当R为0.2 m时,FM-x的弯曲损耗约为1.75 dB/m,FM-y的弯曲损耗约为0.45 dB/m,比普通阶跃型大模场光纤要小得多,其基模Aeff约为1070µm2.随着弯曲半径的增大,当R大于0.3 m时,FM-x与FM-y的弯曲损耗接近一致.只要保持弯曲半径大于0.38 m,弯曲损耗就可以小于0.1 dB/m,基模Aeff可以保持在1047µm2左右.对比文献[8],这种光纤结构的基模有效面积大大提高,而弯曲损耗却并没有增加很多,这是由于左右两侧空气孔的限制,使光纤基模模场不易泄漏到光纤包层区域,从而保证了光纤的大模场低弯曲损耗特性,光纤基模模场被很好地限制在了纤芯内部.

图9 (a)光纤基模弯曲损耗;(b)有效面积随弯曲半径的变化曲线

图10 弯曲半径为(a)0.18 m;(b)0.38 m;(c)0.58 m时的基模模场分布图

图10 是光纤弯曲半径为0.18,0.38,0.58 m时光纤基模x偏振态的模场分布图.随着弯曲半径的减小,光纤形变量增大,光纤基模模场逐渐偏离纤芯,向包层区扩散,使得光纤模场面积增大.

由于双空气孔的增加,使得光纤模场形状变成类矩形,在实际应用中若只用于大容量传输,或与相同类型的有源光纤相连接,其模场形状对实际应用并无影响,只需利用保偏熔接机对准熔接即可.若与普通光纤熔接,则应考虑损耗问题.这是由于普通光纤的模场形状大多为圆形类高斯型,当与其熔接时模场会有不匹配的问题.

6 结论

本文提出了一种新型双空气孔多芯-双模-大模场面积光纤结构,计算了其模场分布、基模有效面积及弯曲损耗特性,分析了各结构参量对有效折射率及基模有效面积的影响.提出了一种新的定义—–双模传输.研究发现,这种结构可以在二阶模数目减少为两个的同时实现大模场面积传输,基模有效面积约为1044µm2.调整结构参量甚至可以达到单模传输.光纤外层涂高折涂覆时,弯曲损耗比普通阶跃型大模场光纤要小得多.合理设计各结构参量,可使基模有效面积达到3512µm2甚至更高,从而满足光通信领域中大容量、高功率传输等实际应用的需求.这种光纤不需要复杂的包层结构,只需利用光子晶体光纤的制作工艺—–管棒堆积法即可,制作方法比一般大模场光纤更简单.这种结构不仅适用于无源光纤的大容量传输,而且可用来制作有源光纤,用于大功率光纤放大器及激光器中.

[1]Qian D,Huang M,Ip E,Huang Y,Shao Y,Hu J,Wang T 2011 Optical Fiber Communication Conference(OFC)Los Angeles,USA,March 6,2011 pPDPB5

[2]Akihide S,Hiroji M,Takayuki K,Masamichi F,Kengo H,Eiji Y,Yutaka M,Munehiro M,Masato M,Hiroshi Y,Yohei S,Hiroyuki I 2010 Optical Fiber Communication Conference(OFC)San Diego,USA,March 21,2010 pPDPB7

[3]Cai J X,Cai Y,Davidson C,Lucero A,Zhang H,Foursa D,Sinkin O,Patterson W,Pilipetskii A,Mohs G,Bergano N 2011 National Fiber Optic Engineers Conference(NFOEC)Los Angeles,USA,March 6,2011 pPDPB4

[4]Masanori K,Kunimasa S,Yasuo K 2009 IEICE Electron.Express 6 98

[5]Fini J M,Zhu B,Taunay T F,Yan M F 2010 Opt.Express 18 15122

[6]Tetsuya H,Toshiki T,Osamu S,Takashi S,Eisuke S 2011 Opt.Express 19 16576

[7]Xia C,Bai N,Ozdur I,Zhou X,Li G 2011 Opt.Express 19 16653

[8]Moritz M V,Marwan A A,Andreas V,Thomas G 2009 Opt.Lett.34 2876

[9]Fini J M 2011 Opt.Express 19 4042

[10]Zhu B,Taunay T,Fishteyn M,Liu X,Chandrasekhar S,Yan M,Fini J,Monberg E,Dimarcello F 2011 Optical Fiber Communication Conference(OFC)Los Angeles,USA,March 6,2011 pPDPB7

[11]Yaman F,Bai N,Zhu B,Wang T,Li G 2010 Opt.Express 18 13250

[12]Baggett JC,Monro T M,Furusawa K,Finazzi V,Richardson D J 2003 Opt.Commun.227 317