基于磁流体填充微结构光纤的温度特性研究*

2013-12-12苗银萍姚建铨

物理学报 2013年4期

关键词：磁流体包层纤芯

苗银萍姚建铨

1)(天津理工大学电子信息工程学院,天津薄膜电子与通信器件重点实验室,天津 300084)

2)(天津大学激光与光电子研究所,天津大学精仪学院,天津 300072)

(2012年7月27日收到;2012年9月8日收到修改稿)

1 引言

微结构光纤(microstructured optical fiber,MOF),又称光子晶体光纤(photonic crystal fiber,PCF),是一种在横截面方向上由紧密排列的波长量级空气孔构成的微结构包层的新型光纤[1].微结构光纤包层的空气孔可以看成一系列功能材料的反应器,为填充各种功能材料提供了空间和自由度,大大拓展了微结构光纤的应用.若将具有电光、热光、磁光、声光和非线性等特性的功能材料填充到特殊设计的MOF中,能够通过施加外场改变功能材料的物理特性,实现微结构光纤传导机制和特性的调谐和控制,进而能够实现基于电、热、光、磁、声等外场操控的可调谐新型光纤光子功能器件.目前,研究人员根据液晶具有良好的电光、热光等特性制备了电调谐光纤光子器件[2−6],通过填充高折射率聚合物,不仅可以对其温度调谐,还可以改变光纤的传导机制等[7,8];Kawanishi等[9]对空芯光子带隙光纤的纤芯大空气孔中填充了PbSe纳米晶体量子点材料,利用1535 nm处10 mW的抽运光实现了1554 nm处的受激辐射;石墨烯的可饱和吸收特性也常常被用于光纤激光器的锁模应用之中[10];科学家还将半导体芯片嵌入微结构光纤中,制造出一种具有高速光电功能的新型光纤[11];Du等[12]将金纳米线选择性填充到高双折射微结构光纤的包层空气孔中,实现了不同偏振方向的波长滤波特性;等等.上述研究表明通过合理设计微结构光纤的结构和选择合适的填充材料可以获得许多新的特性,能够实现各种新型光纤器件.2006年Psaltis等[13]提出微流体波导器件的技术后,微流体光子器件以其可调、可控、可重组等独特的优点引起人们的极大关注,其中,以磁流体为代表的微流体材料应运而生.

磁流体是一种光学性质随外界环境改变的新型纳米功能材料,一般是由纳米级的强磁性颗粒高度弥散于某种载液之中形成的稳定胶体.磁流体既具有固态磁性物质的磁性,又有着液态物质的流动性.理论和实验研究证明,该材料的复杂多变的微结构使其具有各种优异的可调谐光学性质,也为新型光子器件的设计提供了极大的可能.研究人员已经利用磁流体独特的热光效应和磁光效应制作了高性能可调谐光子器件,如光调制器、光开关、波分复用器、可调谐光栅、可调谐滤波器等[14−17].最近将其填充到MOF中,分析了其磁光效应对光纤传导特性的影响并实现了对光谱的调谐[18−21].然而在实际应用中与布朗热运动有关的热光效应尤为重要[22−26].当温度升高或降低时,Fe3O4颗粒的分布与排列发生变化,从而导致液体的光学特性随之变化.磁流体的热光系数约为−2.4×10−4/°C[27],比光纤的二氧化硅材料的热光系数(+8×10−6/°C)高出两个数量级.两者之间较大的热光系数差异,为磁流体与光纤的结合创造了条件,使其可作为具有特殊热光效应的功能材料用于全光纤光子器件等领域.

本文基于磁流体的热光效应,将其与MOF有机地结合起来,并对填充的MOF的光谱特性和温度敏感性进行了研究.结果表明由于磁流体本身特性,填充后该材料没有改变光子晶体光纤的传导机制,依然为折射率引导型;在波长为600—1700 nm之间透射功率和长波边缘的光谱特性对温度非常敏感,温度敏感度达到0.06 dB/°C,且由于磁流体载液与表面活性剂对温度的不同敏感性,实现了对透射谱的单边调谐.因此,将其作为热光可调谐器件以及温度传感器等光纤光子器件将具有很大的应用潜力.该研究可为探索新型全光纤光子器件的新技术和新结构提供有效的方法.

2 实验

研究中所使用的光纤为长飞公司提供的六角形空气孔MOF,其包层由五层三角栅格周期排布的空气孔组成,在纤芯处缺失一个空气孔引入缺陷而形成石英纤芯,其中,空气孔直径为3.67µm,孔间距为6.36µm,纤芯直径为8.8µm,光纤的横截面如图1所示.纤芯由二氧化硅构成,折射率为1.462914,空气孔的出现降低了包层的平均折射率,因此光纤的纤芯折射率高于包层折射率,在导光机制上属于折射率引导型微结构光纤.

利用化学共沉法配制的水基Fe3O4溶液作为填充的磁流体,它由直径约为10 nm的Fe3O4磁性颗粒、包裹于其上的表面活性剂以及溶剂水组成,浓度为1 mg/mL,磁饱和强度为0.96 emu/g,纳米颗粒的透射电子显微镜(TEM)结果如图2所示.纳米量级的颗粒直径使得Fe3O4磁性颗粒可通过布朗运动均一稳定地分散开来,从而使它们对溶液的整体磁性反应起作用,表面活性剂用于防止铁磁颗粒由于范德华力和磁力作用而发生凝聚.配制好的磁流体的折射率约为1.34,低于所要填充的六角形MOF的纤芯折射率1.462914,因此光纤填充磁流体后,不改变原来的导光机制.在没有外加磁场的情况下,磁流体表现出各向同性的光学特性.

图1 六角形空气孔光子晶体光纤横截面

图2 水基Fe3 O4磁流体TEM

本研究采用低压抽入的方式将磁流体填充到MOF的包层空气孔中,填充速度与磁流体的黏滞度、光纤空气孔的大小以及填充时气压差的大小有关,实验中得到的平均填充速度约为1 cm/min,填充长度由填充时间决定.由于填充和未填充的光纤区域,其侧面对光的反射效果不同,因此在显微镜下能够清晰看到功能材料的填充位置,如图3所示.然后将填充后的微结构光纤的两端与单模光纤熔接起来,总体损耗约为10 dB.

图3 空气孔微结构光纤填充后显微镜下侧面图

3 磁流体填充微结构光纤的透射谱分析

3.1 磁流体填充微结构光纤的透射谱

将两端熔有单模光纤的磁流体填充微结构光纤的一端接超连续光源(超连续光源光谱如图4所示),一端接入光谱仪(光谱仪为ANDO ELECTRIC公司生产的AQ6317B型).为了排除光源波动对实验结果的影响,将输出光谱对光源原光谱做减法处理,以获得不受光源影响的相对的光纤透过率曲线.磁流体填充长度约为5 cm的六角形空气孔微结构光纤在室温下的透射谱如图5所示.在1460 nm处,可观察到一个明显的吸收峰,这是由Fe3O4纳米颗粒、表面活性剂和载液三者吸收峰的叠加引起的.

图4 超连续光源光谱图

图5 室温下磁流体填充长度5 cm的微结构光纤透射谱

3.2 磁流体填充长度和浓度对微结构光纤透射谱的影响

图6 填充长度和磁流体的浓度对光纤透射谱的影响 (a)不同填充长度下的透射谱;(b)填充不同浓度磁流体时的透射谱

对填充不同长度、不同浓度磁流体的MOF透射谱进行了比较,如图6所示.图6(a)中的两个透射谱填充的磁流体浓度相同,填充长度不同,分别为5和10 cm.实验结果表明,填充后的光纤的吸收峰位置不受填充长度的影响,填充长度越长,吸收峰越深,这是因为光与磁流体的作用区域越长,在磁流体中损耗的光能便越多.图6(b)对填充不同浓度的微结构光纤的透射谱进行对比,填充时间均为5 min.其中“强”谱线所填充的磁流体浓度约为“弱”谱线的20倍.同样,磁流体的浓度也不会影响吸收峰的位置.理论上,磁流体浓度越大,对光的吸收越多,造成的吸收损耗也就越大.但在填充时间相同的情况下,浓溶液由于具有较大的黏滞系数,导致其填充的长度较短,因此在透射谱中浓溶液表现出较低的透射损耗.

4 磁流体填充微结构光纤的温度传感特性分析与讨论

由于磁流体具有较高的热光系数,填充磁流体将大大提高MOF的温度灵敏度.将其置于温控箱中研究该光纤的温度传感特性,实验装置如图7所示.为了避免弯曲带来的实验误差,MOF的填充部位被固定在有机玻璃板上.温度传感特性选定波长测量范围为1100—1600 nm,温度变化范围为27°C—98°C,填充长度约为5 cm.

图8给出了不同温度下光纤透射谱的变化情况.从图8中可以看出,随着温度的上升,透射谱中磁流体吸收峰深度逐渐变浅,而吸收峰波长保持不变.当纤芯传导的光与磁流体填充区域存在模场交叠时,光与液体将会发生相互作用,部分光能量会被磁流体吸收而产生损耗,表现为透射谱中的吸收峰.磁流体溶液中实现吸收的物质包括三部分:Fe3O4磁性颗粒、表面活性剂以及载液.该吸收峰是由三者各自对光吸收峰的叠加而形成.由于这三种物质的吸收谱形状、对光的吸收作用随温度的变化不同,因此叠加后的吸收谱在温度变化的过程中,左右两个边沿表现出不同的温度响应.如图8所示,吸收峰左边缘基本保持不变,而长波边缘透过率随温度的升高单调增大.

图7 磁流体填充微结构光纤温度传感实验装置

图8 磁流体填充微结构光纤透射谱随温度的变化

磁流体对光能的吸收除了与填充材料本身特性有关外,在很大程度上还依赖于光纤截面上光场与磁流体区域的交叠面积,两者之间的交叠面积越大,光能和磁流体的相互作用就越充分,磁流体对光能的吸收也就越多.在填充后的MOF中,磁流体位于空气孔中,位置固定,交叠面积完全取决于光纤纤芯中的光场模场面积,只有当纤芯中的模场足够大以致扩散到空气孔区域,才有可能产生光能的吸收损耗.而光场的模场面积与光纤本身的导光性能有关,这里,光纤仍属于折射率引导型,纤芯对光场的束缚能力直接决定于光纤纤芯与包层之间的折射率差.该差值越大,纤芯对光场的束缚能力越强,光能被牢牢束缚在纤芯中,模场面积也就越小,从而使光场与磁流体区域的交叠面积减小;反之,差值越小,光场与磁流体区域交叠面积越大.温度对构成光纤的二氧化硅材料以及填充在光纤包层空气孔中的磁流体的折射率均有调节作用,但调节幅度却大大不同,二氧化硅材料的热光系数比磁流体的热光系数小两个数量级,也就是说,当改变环境温度时,光纤材料折射率的变化程度要远远小于磁流体,因此在分析过程中,可以只考虑磁流体给整个光纤导光性能带来的影响,光纤本身作用可忽略不计.由于磁流体的热光系数为负值,因此,当温度上升时,其折射率数值减小,从而使整个包层的平均折射率降低,纤芯与包层之间的折射率差增大.增大的折射率差会加强光纤对纤芯模式的约束能力,模场面积减小,与此同时,光场和磁流体填充区域的交叠面积也随之减小,磁流体对输入光的吸收损耗降低.

表1给出了通过Comsol multiphysics软件对不同温度下,纤芯中传导的基模在吸收峰1460 nm处的有效折射率和损耗的理论计算值,我们对20°C,70°C,120°C,520°C等较大的温度变化情况进行了计算.结果表明,随着环境温度的上升,光纤的损耗在逐步减小,这说明光纤对光场的束缚能力不断增强,与上述分析相符合.尤其是作为纤芯模式的基模,其有效折射率也会受到包层磁流体折射率的影响,当磁流体的折射率随温度的上升而降低时,基模的有效折射率也在减小,这进一步说明基模并没有完全禁锢在纤芯当中,而是部分扩散到了填充区域,这也正是损耗产生的原因.

表1 不同温度下的光纤基模有效折射率和损耗

根据温度实验结果,图9给出了透射谱在吸收峰值1458 nm处透过率随温度的变化规律.从图9中可以看出,透过率(或磁流体吸收损耗)和温度之间成一次函数关系,灵敏度为0.045 dB/°C,直线拟合表达式为

其中,P为透过率,T为温度,单位分别为dB和°C,线性度0.999.该温度实验结果经过了若干次的重复实验,具有可靠的重复性.

为了进一步探究磁流体填充长度对其温度特性的影响,研究中也制作了填充长度约为10 cm的MOF.图6(a)中表明,不同的填充长度仅影响光纤的整体损耗,不影响光纤透射谱的谱形以及磁流体吸收峰的峰值波长.磁流体填充长度增加后,光与磁流体的交互作用区域更大,对光的吸收更多,因此,在光谱上表现出填充长度越长磁流体吸收峰越深的规律.

图9 磁流体填充微结构光纤透过率与温度的关系

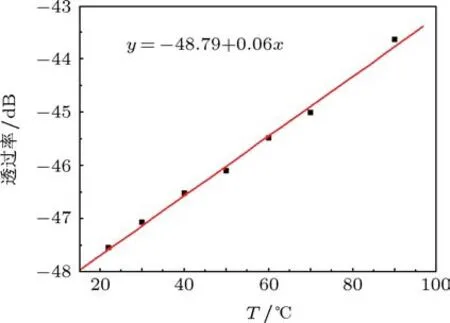
图10 磁流体填充微结构光纤透过率与温度的关系

该填充长度的光纤具有与前者相似的温度特性,光纤的透过率和温度之间具有较高的线性关系,如图10所示,一次函数拟合表达式为

其线性度为0.996.该微结构光纤的温度灵敏度达到0.06 dB/°C,高于之前填充长度5 cm的微结构光纤的灵敏度0.045 dB/°C,可见,填充长度越长,相当于参与通过温控调谐包层折射率的功能材料越多,因此,温度灵敏度越高.

5 结论

本文基于微结构光纤横向结构的高度可集成特性,利用普通毛细作用的填充方法将纳米磁流体材料完全填充到折射率引导的微结构光纤的包层空气孔中,并分析了其传导特性及温度敏感特性.其中填充的长度分别为5和10 cm,并将两端与普通单模光纤进行熔接,损耗约为10 dB.该液体填充后不改变光子晶体光纤的传导机制.基于磁流体载液与表面活性剂对温度的不同敏感性,结果表明在波长为1100—1700 nm之间透射功率和长波边缘的光谱特性对温度非常敏感,温度敏感性达到0.045 dB/°C,该研究将微结构光纤与磁流体材料有机地结合起来,并利用填充材料自身的热光特性,实现了对透射谱的单边调谐,将其作为热光可调谐器件、滤波器等相关可调谐光子器件在光通信、光传感等领域将具有很大的应用潜力.基于材料填充微结构光纤的研究可为探索新型全光纤光子器件的新技术和新结构提供有效的方法.该研究可为探索新型光纤光子器件的新技术和新结构提供有效的方法.

[1]Birks T A,Knight J C,Russell St P J 1997 Opt.Lett.22 961

[2]Lee C,Chen C,Kao C,Yu C,Yeh S,Cheng W,Lin T 2010 Opt.Express 18 2814

[3]Wei L,Alkeskjold T T,Bjarklev A 2010 Opt.Lett.35 1608

[4]Wang Y P,Jin W,Jin L,Tan X L,Bartelt H,Ecke W,Moerl K,Schroeder K,Spittel R,Willsch R,Kobelke J,Rothhardt M,Shan L,Brueckner S 2009 Opt.Lett.34 3683

[5]Steinvurzel P,Moore E D,M¨agi E C,Eggleton B J 2006 Opt.Lett.31 2103

[6]Kerbage C,Hale A,Yablon A,Windeler R S,Eggleton B J 2001 Appl.Phys.Lett.79 3191

[7]Bise R T,Windeler R S,Kranz K S,Kerbage C,Eggleton B J,Trevor D J 2002 Proceedings of the Optical Fiber Communications Conference Anaheim,USA,March 17–22,2002 ThK3

[8]Larsen T,Bjarklev A,Hermann D 2003 Opt.Express 11 2589

[9]Kawanishi S,Komukai T 2007 Lasers and Electro-Optics Baltimore,USA,May 6–11,2007 p4453012

[10]Choi S Y,Cho D K,Song Y W 2012 Opt.Express 20 5652

[11]Rongrui H,Pier J A S,Anna C P,Noel H,Justin R S,Mahesh K,Venkatraman G,John V B 2012 Nature Photonics 6 174

[12]Du Y,Li S G,Liu S 2012 Chin.Phys.B 21 94219

[13]Psaltis D,Quake S R,Yang C 2006 Nature 442 381

[14]Huang Y W,Hu S T,Yang S Y,Horng H E,Hung J C,Hong C Y,Yang H C,Chao C H,Lin C F 2004 Opt.Lett.29 1867

[15]Horng H E,Chieh JJ,Chao Y H,Yang S Y,Hong C Y,Yang H C 2005 Opt.Lett.30 543

[16]Pu S,Chen X,Chen Y,Xu Y,Liao W,Chen L,Xia Y 2006 J.Appl.Phys.99 093516

[17]Trigt C 1997 J.Opt.Soc.Am.A 14 741

[18]Thakur H V,Nalawade S M,Gupta S,Kitture R,Kale S N 2011 Appl.Phys.Lett.99 161101

[19]Candiani A,Konstantaki M,Margulis W 2010 Opt.Express 18 24654