基于线段操作的多边形求交算法研究

鲍其胜，王 庆，何立恒

(1.南京市测绘勘察研究院有限公司，江苏南京210005;2.南京林业大学土木工程学院，江苏南京210037)

两个多边形求交是计算几何的基本问题之一，应用十分广泛。地图制图中的图面要素压盖处理、地理信息系统中不同类别多边形拓扑叠加分析、计算机辅助设计中的文字、图块消隐等都直接或间接地用到多边形求交［1-3］。在进行土方计算时，需要将计算边界之外的格网删剪掉，实际也是多边形求交。边界外框是由边界点坐标系列中(Xmin，Ymin)为左下角、(Xmax，Ymax)为右上角的矩形，计算边界包含于边界外框内。对边界范围内的区域计算，以计算边界外框循环得到的格网跟计算边界有相交、包含和分离3种关系。为了摒弃计算边界范围外的网形，需要进行所构网形与边界的相互关系判别并求交，得到边界内的网形。

一、几个关系判别算法

1.多边形相互关系判别

本文所讨论的多边形是在同一水平面或投影到同一水平面上的简单多边形，多边形相互关系判别如图1所示。将多边形看做是封闭的线实体，通过求线实体的交点个数来判断两个多边形的相互关系。若没有交点，则为包含或分离(非包含);若有交点，则为交叉关系。包含和分离关系的判定实质是点与多边形的关系判定，若顶点都在计算边界范围内，则是包含关系;若顶点都不在计算边界内，则是分离关系。

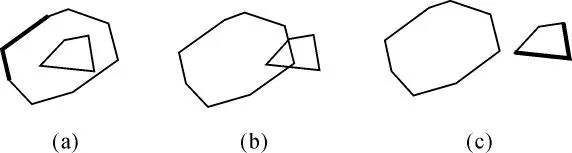
图1 多边形相互关系示意图

2.点和多边形相互关系判别

在点与多边形相互关系判定中，采用射线交点法进行判定［4-5］。以待判定点为起点作任意射线，通过射线与多边形边界交点的奇偶性来确定，若交点数为奇数，则点在多边形内;若交点数为偶数，则在多边形外。通常射线由一段超出多边形范围的水平线段代替，此线段的一端点为待判定点，另一端点则是水平向右或向左的多边形范围外任一点，如图2所示。但图3是交点为多边形顶点的情况，此法则失效。因此，在判定之前，要明确点是否在多边形的边界上。图3中，图3(a)有1个交点，图3(b)有3个交点，图3(c)有4个交点，图3(d)有2个交点，仅以交点的奇偶数进行判别，图3(b)、图3(d)与事实不符。因此，在实际计算交点个数时，要特别判定交点是否为多边形的一个顶点或在多边形线段上。因此，设定一原则，多边形以交点为线段一端点的两连续线段位于射线左右来制定，位于两侧的为1个交点，位于同侧或线上的为0个交点或2个交点。

图2 点和多边形相互关系示意图

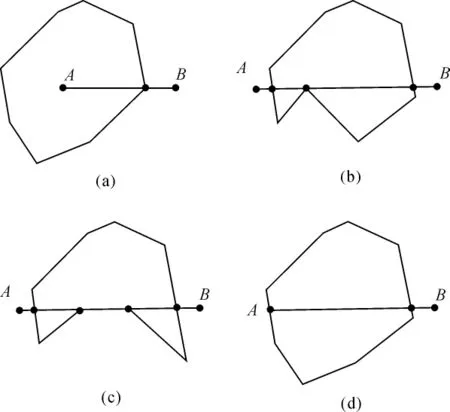
图3 点在多边形内外判定交点几种特殊情况

二、求交叉关系算法与实现

1.算法思路

国内外研究人员对多边形求交作了深入研究。杨维芳［6］给出两数组记录交点后，对数组遍历求交;朱爱军等［7］在交点序列基础上扩充成节点序列，通过遍历序列求交;杜爽等［8］在交点结构中记录与交点相关的节点信息，如出入状态、交点位置等来求解;宋立明等［9］采用双向链表数据结构，对两简单多边形的顶点及交点进行插入存储，通过遍历两个顶点、交点混合表来达到求交目的。上述研究的核心都是求出多边形交点，然后进一步对点操作，本文则另辟蹊径，在求出多边形交点后，对由多边形节点和交点组成的子线段进行操作，判断所构成的子线段是否属于公共线段，以构成公共线段集，遍历公共线段，连接成闭合多边形求交。

2.算法过程

图4有两个多边形M、N，求交叉公共多边形需分步进行。

1)选择多边形并判定两多边形的相互关系。将平面M作为目标多边形，平面N作为源多边形。利用交点个数判断两多边形的相互关系，若相交，继续下一步;若分离，结束计算;若包含，留下被包含图形后结束计算。

2)求交点。选取目标多边形M中线段M1M2与源多边形N的每条线段求交点，若线段M1M2与源多边形N边界有交点，将所有交点去掉重复点后，连同从目标多边形所选定线段M1M2的端点按此线段的一定方向排序，如图4所示，M1、P1、…、Pn、M2为排序的系列点。其中，M1、M2为目标多边形的线段端点;P1、…、Pn为线段M1M2与源多边形N的所有交点。

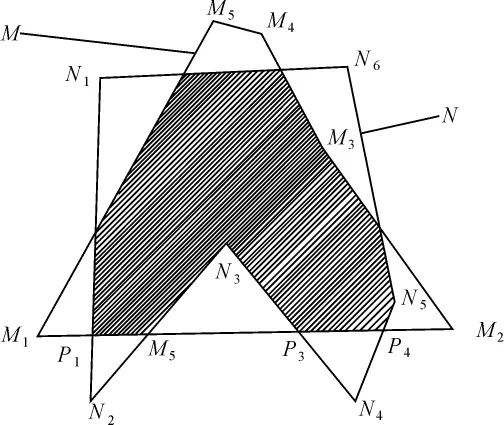
图4 求公共面

两线段p1p2和q1q2交点一般为图5几种情形，本算法中的交点个数分别为：图5(a)为J一点，图5(b)为p2一点，图5(c)为p2(或q1)一点，图5(d)为p2和q1两点，图5(e)为p1和p2两点，图5(f)为q1(或p1)和q2(或p2)两点。

图5 线段交点关系图

3)找公共线段。将端点和交点依顺序两两作子线段，即 M1P1、P1P2、…、PnM2为依次连接的线段，求各线段的中点，根据点在多边形内外判定方法判断中点与源多边形N的相互关系，若线段的中点在源多边形内或在源多边形边界上，则此线段也在源多边形内或在源多边形边界上，此线段即为公共线段，将此线段及线段的两个端点坐标记录在数据选择集中，直至所有两两点连成的线段判定完毕。图4中线段P1P2和P3P4即为公共线段。

4)选取构成目标多边形M的下一个线段，重复步骤2)和步骤3)，直至构成目标多边形M的所有线段与源多边形N求交点计算完毕，然后判断各相邻点连成的线段是否在源多边形内或边界上，若在源多边形内或边界上，即为公共线段并记录至公共数据选择集中。

5)将目标多边形和源多边形对调，原源多边形作为目标多边形，原目标多边形作为源多边形，重复步骤2)～步骤4)。进行步骤3)操作时，若线段的中点在源多边形内，记录至公共线段;若线段的中点在源多边形边界上，因目标多边形和源多边形对调前已记录，对调后将不再记录，避免重复。

6)遍历公共线段，构建两多边形交集。从公共线段数据选择集中取出任一线段，根据此线段端点坐标，在公共线段数据选择集中找与其首尾相连的线段，将它们连接起来，依次找出与连接图形端点相同的其他线段并连接，组成封闭多边形。在寻找过程中，选中的线段就从公共线段数据选择集中删掉。

7)若组成一个封闭多边形后，公共线段数据集中还有线段，重复步骤6)，直至公共线段数据集中没有线段，此时构成的所有封闭多边形即为所求的两多边形交集。

三、算法分析比较

1)本算法是在求交点后，组成子线段进行判断并求交，判断过程中已考虑重边或重点等问题。杨维芳［6］使用数组只能表示一个交点，对重边有两个交点的不能表示;朱爱军、杜爽等［7-8］采用交点序列或出入状态判别，过程复杂，尤其对重边、重点要单独考虑，显得繁琐;宋立明等［9］采用了双向链表数据结构，没有解决重边或重点问题。

2)上述已有算法的记录方式都有两组数组、序列或链表，探测对象是节点，探测方向都是在两组存储数据中转换。本算法采用由节点和交点组成的子线段为探测对象，形成一组公共线段集，遍历公共线段数据集求交，探测对象及探测方法包罗了重边或重点的情况。

3)从算法的时间上比较，求交点与已有算法基本一致;在探测每一线段及交点时，已有算法只对交点操作，本算法探测节点和交点组成的子线段，每条边多一次探测，总共多出两多边形边数总和;在遍历时间上，本算法只对公共线段数据集遍历，明显比已有算法要短;总体时间与已有算法相当。

4)在存储单元上，本算法存储的是公共线段，已有算法存储的是节点和交点，本算法远优于已有算法。

5)本算法在进行子线段探测时，只需改变探测条件，即可实现两多边形的求差和求并。

四、结束语

本算法过程简单、思路严谨，考虑到地图的复杂性和特殊性，运算结果精度和图形输出质量高。若算法基于AutoCAD平台来实现，利用二次开发工具VBA中object.IntersectWith函数的返回值求交点个数及交点坐标，使得计算过程更简单，运行效率更高。连线利用AutoCAD中的数据选择集，在数据存储空间上和搜寻时间上效率又一步得到提高。

求公共面算法主要是针对计算机地图制图、地理信息系统、计算机辅助设计等领域中多边形求交，即着重于地图上多边形的交集运算。本算法易于编程实现，计算工作量小，求交效率高，已成功应用在土方计算软件开发中，在计算机图形和地理空间信息等方面可以广泛应用。

［1］谢忠，魏东琦，吴亮，等.简单矢量数据多边形裁剪问题的图模型［J］.测绘学报，2009，38(4)：369-374.

［2］刘勇奎，高云，黄有群.一个有效的多边形裁剪算法［J］.软件学报，2003，14(4)：845-856.

［3］彭杰，刘南，唐远彬，等.一种基于交点排序的高效多边形裁剪算法［J］.浙江大学学报：理学版，2012，39(1)：107-111，122.

［4］董秀山，刘润涛.判断点与简单多边形位置关系的新算法［J］.计算机工程与应用，2009，45(2)：185-186.

［5］陈瑞卿，周健，虞烈.一种判断点与多边形关系的快速算法［J］.西安交通大学学报，2007，14(1)：59-63.

［6］杨维芳.两个复杂多边形求交的矢量算法［J］.兰州铁道学院学报：自然科学版，2002，21(1)：108-110.

［7］朱爱军，邓安福，魏艳军，等.以节点操作确定两任意实心多边形交集的方法［J］.重庆大学学报：自然科学版，2004，34(12)：56-59.

［8］杜爽，陈成永.以节点操作实现多边形求交的算法［J］.测绘通报，2007(10)：21-24.

［9］宋立明，闫浩文，王邦松，等.两个简单多边形求交的算法［J］.测绘与空间地理信息，2011，34(1)：258-260.

［10］张帆.AutoCAD VBA二次开发教程［M］.北京：清华大学出版社，2006.