三维场景建模中地物与地形匹配方法研究

江 禹，李永树，鲁 恒，张帅毅

(西南交通大学地理信息工程中心，四川成都610031)

一、引 言

传统的GIS通常以二维方式展现空间数据，而二维GIS本质上是抽象的地图符号系统，不能给人以自然界的真实感受。随着GIS理论与技术、虚拟现实、计算机图形学等技术的不断发展，越来越多的GIS系统开始通过构建三维场景来表现和模拟现实环境，弥补了二维GIS的不足，如虚拟城市、数字校园和虚拟战场等。

目前，二维数据构建三维场景的方法大致分为：基于纹理的方法和基于几何的方法。基于纹理的方法是将纹理数据(如数字正射影像)映射到地形，这种方法适合于大范围粗略构建三维场景，但本质上是一种二维的方法，无法精确表达三维地物，且真实感不足［1］;基于几何的可视化方法是将三维地物模型集成到地形表面，为满足真实感、沉浸感的要求，三维场景中的地物(如房屋、道路等)不仅要如实地表现其几何形状和基本特征，而且还要和三维地形实现完美匹配，以满足用户视觉和心理学的要求［2］。然而在实际应用中，三维模型采取地物与地形分离建模的方式，对于地物的三维模型，其地物的XY坐标序列是严格地按照地理坐标获取，其高程Z是地物的真实高程;对于地形模型，无论采用不规则三角网模型(TIN)还是规则格网模型(RSG)，构建的地形与现实地形还存在一定偏差，且在构建地形过程中没有考虑地物地表特征(如房屋基座水平等)的约束信息［3］。因此，按照这种分离建模后将地物与地形集成的方法，其结果可能出现地物与地形不匹配的现象。以房屋为例，可能出现房屋悬在空中或者陷入地表等情况，如图1所示。为了使地物与地形一致，在三维场景建模中就需要考虑地物与地形的匹配问题。

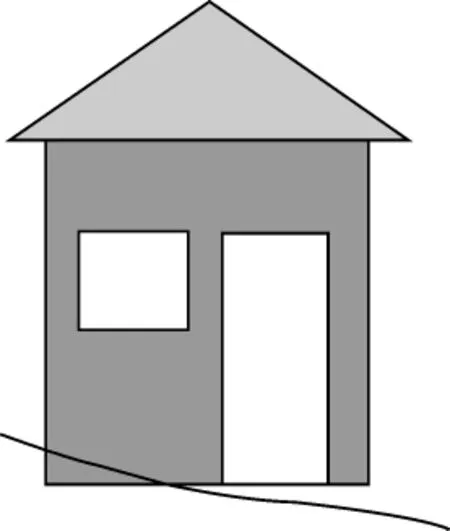
图1 房屋与地形不匹配现象

二、地物与地形匹配的两种策略

根据地物与地形的关系，可以将地物划分为两大类：一类是独立于地形的地物，它们与地形是相对位置的关系，如树木、路灯等;另一类是依赖于地形的地物，这类地物与地形密不可分，如房屋、河流、道路等。因为这两类地物的性质不同，所以采取的匹配策略也不同［4］。

1.独立于地形的地物模型与地形的匹配策略

这类地物从几何形态上可以看作是点状模型，它与地形的关系主要是空间位置关系。这种情况应采取地物适应地形的思路，只要做到空间位置配准即可。这种匹配方法的实现比较简单，主要通过调整地物的位置和姿态，或者延伸地物基座填充与地形之间的空隙，实现其与地形的匹配，如图2(a)所示。但这种匹配策略仅限于可以将地物看作点状模型的情况，在精密三维场景建模中适用范围有限，本文不作深入探讨。

2.依赖于地形的地物模型与地形的匹配策略

这类地物在几何形态上呈现为面状，与地形的起伏走向关系密切。对于此类地物与地形的匹配，应该充分考虑到地物对地形的影响，采取地形适应地物的思路，如图2(b)所示，改造局部地形以适应房屋。近年来，国内外学者针对地物与地形匹配的解决方法，采用的也主要是地形适应地物的思路。刘宁、王光霞分别在文献［4］和文献［5］中提出了利用多边形裁剪算法进行地物与地形匹配，该算法主要应用于道路与地形的匹配，对于房屋与地形的匹配算法较复杂，且该算法针对的是规则格网模型;蒲浩、郑顺义分别在文献［6］和文献［7］中将三维地物基座作为约束线和约束点添加到TIN中，通过约束Delaunay三角网的构建实现地物与地形的无缝匹配，但约束线和约束点的插入可能导致地形局部突变。

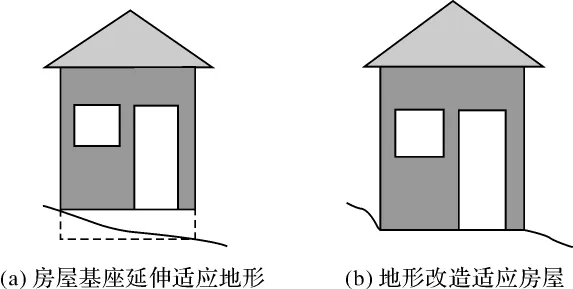
图2 地物与地形匹配的两种策略

针对以上问题，本文根据TIN模型，采取地形适应地物的思路，提出了一种改进的地物与地形匹配方法。在地形模型构建完成后对TIN进行部分重构，实现地物与地形的无缝匹配，同时对匹配后可能出现的地形突变情况进行了地形的局部修正，此种方法主要适用于精密三维场景建模中面状地物(如房屋)与地形的匹配。

三、改进的地物与地形匹配方法

在表现数字地面模型时，TIN比RSG更能反映原始地形的细节，特别是当地形包含大量地物特征线时，TIN能更好地顾及这些特征，从而更精确合理地表达地表形态［8］。目前，业界公认Delaunay提出的构建TIN的算法较优，它尽可能地避免了病态三角形的出现。利用Delaunay三角网中每个三角形外接圆都不包含点集中的其他任意点这个特性，就可以直接构成Delaunay三角网［9］。

1.考虑地物特征的Delaunay三角网重构

(1)地物特征的提取

地物特征提取是为了将地物特征看作约束条件插入地形，实现地物地形融为一体，所以只需提取地物与地形相接部分的特征即可。以房屋与地形的匹配为例，地物特征就是房屋基座多边形的所有边和顶点在平面二维Delaunay三角网上的投影，房屋的高程取基座的实测高程或房屋基座在TIN上投影所围成多边形的平均高程。

(2)嵌入地物特征点约束

某房屋的基座在Delaunay三角网中的投影为多边形 Polygon，横跨多个三角形，地形特征点集(Polygon的顶点集合)Nodes={A，B，C，D，E，F}，地形特征线集 Edges={AB，BC，CD，DE，EF，FA}，包含在房屋基座内部的三角网顶点集P={11}，基座多边形的三角网凸包为顶点集 Box={6，7，8，9，10}，参与重构(与凸包Box相邻接)的三角网范围为顶点集 Extent={0，1，2，3，4，5}，称为重构范围，如图3(a)所示，原始TIN如图3(b)所示。Delaunay三角网重构步骤如下：

1)分解重构范围内的三角网。删除多边形Polygon内部的顶点集P及其关联边，删除与凸包顶点集Box相关联的边。

2)插入地物特征点。删除地物特征线集Edges，保留地物特征点集Nodes。

3)重构集的合并。将地物特征点集Nodes和凸包顶点集 Box合并成Delaunay三角网重构集Points，即 Points=Nodes∪Box∪Extent。

4)将重构范围Extent作为初始多边形，依据Delaunay三角网生成的点采用逐点插入法，对重构集Points中的点逐点插入形成Delaunay三角网。

重构后的三角网不能保证地物特征线一定是Delaunay三角形的边，如图3(c)所示。地物特征线BC、CD不是三角形的边，需要在Delaunay三角网重构后将地物特征线作为约束线嵌入Delaunay三角网中，嵌入后如图3(d)所示。

(3)嵌入地物特征线约束

地形中嵌入地物特征线是通过约束Delaunay三角网(CTD)实现的，具体的算法有许多种。本文采用Bernal和Sloan的对角线交换循环算法，其基本原理是：首先不考虑约束条件构建初始Delaunay三角网;其次检查约束边所经过的所有三角形，这些三角形形成的区域称为影响域，影响域中每条三角形的边称为对角线;然后从约束边的起始点出发，如果约束边在影响域内与对角线相交则交换对角线(交换对角线后的三角形不是Delaunay三角形)，否则不作处理，按照此规则循环处理每一个影响域;最终使起始点和目标点相连(图4所示)，使得一条约束边嵌入到三角网中，对每条需要嵌入的地物特征线作上述对角线交换处理，直至所有地物特征线嵌入到三角网中。

图3 考虑地物特征线的Delaunay三角网重构

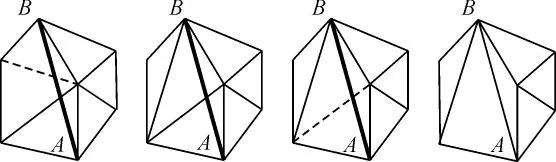
图4 对角线交换循环算法示意图

通过考虑地物特征的Delaunay三角网重构，将地物特征点和特征线嵌入地形，可使得房屋基座多边形内部的高程一致，从而实现地物与地形的无缝匹配。但这种方法会导致地形突变，可能会在地物周围产生明显的“悬崖”或者“台阶”的现象，破坏地形的平滑性，从而使三维场景的真实感削弱。特别是地形变化比较剧烈的情况下，三角网比较密集，这种现象尤为明显，所以需要在嵌入地物特征后对地物周围一定范围内的地形进行局部修正。

2.局部地形修正

所谓地物与地形不匹配实质上是地物高程与地形高程存在差异［9］，考虑地物特征的Delaunay三角网重构通过对地物特征点增加高程改正值，使得地物在基座范围内水平。局部地形修正是将地物特征点的高程改正值扩展为一个修正函数，不仅修改地物特征点的高程，而且对周围的地形进行修正。修正函数表示该点高程变化对周围地形的影响，改正值的大小取决于修正模型的选择。将高程改正值与地形原始高程叠加，产生修正后的地形，就可以在保证地物与地形在完全匹配的前提下使地形自然过渡，如图5所示。

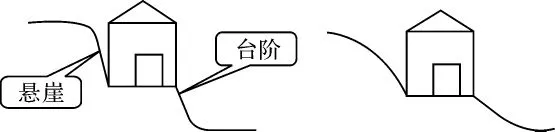
图5 局部地形修正前后示意图

(1)修正模型的确定

一般来说，距离越远，受地物特征点高程变化影响越弱，高程改正值越小;反之则高程改正值越大。满足该特性的任意函数模型都可以考虑作为修正模型。为了实现地形的平滑过渡，本文采用高斯函数模型作为修正模型［10］，其定义为

式中，f(x，y)表示第i个地物特征点在坐标(x，y)处的高程改正值;d为地物特征点到地形影响点的平面距离;hi为第i个地物特征点高程改正值，其值等于地物高程与地形高程之差;exp(-d2/2kh2i)的值从1平滑过渡到0;k为常量，用于控制高斯函数的形状，调节衰减速度，可以根据地形变化的剧烈程度取合适的值。按照该模型确定的修正函数，在地物特征点处的距离d为0，高程改正值最大为hi，随着距离的增加，高程改正值递减，逐渐趋近于0。

(2)地形影响点高程改正值的计算

以地物特征点i为圆心、R为半径搜索周围的TIN节点，在搜索圆Oi内的TIN节点都被确定为受地形特征点i影响的地形影响点，其集合记为Ai。对于Ai内的每个地形影响点，根据式(2)计算出该地形影响点因地物特征点i的插入而产生的高程改正值。

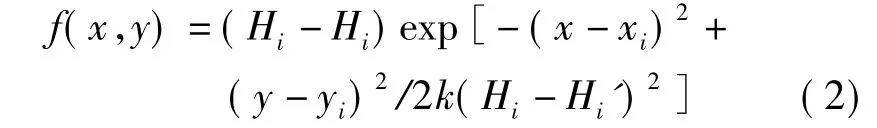
(3)地物特征点影响范围的确定

根据高斯函数的特性，高程改正值随着距离的增加无限逼近于0，意味着对整个地形而言，每个TIN节点都是其地形影响点，地形影响范围为整个定义域。根据高斯函数的分布特性可知，当d＞3khi时高程改正值已经非常接近于0，因此，可以设定地物特征点的影响范围为3khi，即搜索圆的半径R为3khi。通过确定影响范围，将地形的修正限制在一定的范围内，使得算法的运算量减少。

(4)搜索圆相交情况的处理

如图6所示，假设地形影响点p2位于同一地物A的地物特征点i和j的交集之处，与地物特征点i和j的距离分别为di2和dj2，将p2划归到离地物特征点较近的集合，如式(3)所示。

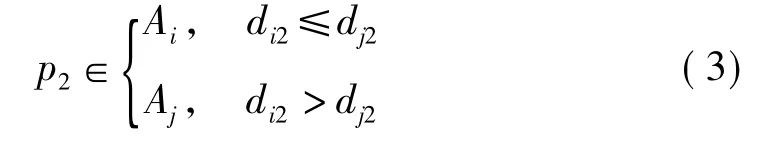
同理，可推导出多个搜索圆相交的情况，即地形影响点受距离最近的地物特征点影响。假设地形特征点i属于地物A，地形特征点j属于地物B，则地形影响点p2的高程改正值受两个地物特征点共同影响，取两地物在该点的修正函数值的平均值。同理，可将其推广至多个地物的地形特征点搜索圆相交的情况。

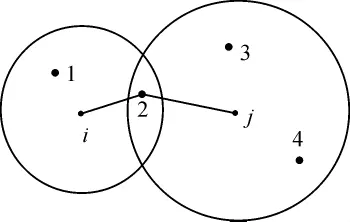
图6 搜索圆相交情况

通过以上步骤确定了每个地形影响点的高程改正值后，将各个地形影响点的高程值加上高程改正值，得到局部修改后的地形。修正后的地形不仅保证了地物与地形的完全匹配，而且过渡自然。局部地形的修正使得在高于原始地形的地物特征点周围生成平滑的山坡，在低于原始地形的地物特征点周围生成平滑凹地，避免了明显的“悬崖”和“台阶”现象，削弱了地形突变影响。

四、实 例

以四川省某地区房屋与地形匹配为例，地形数据来源于低空无人机影像空中三角测量提取的等高线信息，利用等高线的三维坐标序列经处理生成Delaunay三角网。地物特征线和特征点的二维平面信息来源于大比例尺的无人机数字正射影像。地物特征线和特征点的高程值取房屋基座在TIN上投影的平均高程。

以C#.NET和ArcGIS为开发平台，利用本文方法处理TIN模型，进行地形改造，最终的结果在ArcMap中以等高线的形式显示，如图7所示，等高距为2 m。为了使试验结果对比明显，图7中的地形高程进行了2倍拉伸，其中，图7(a)为原始地形，用以做结果对比;图7(b)为考虑地物特征线的Delaunay三角网重构后的地形，其房屋基座范围已经水平，可以实现与房屋的无缝匹配，但房屋基座附近等高线密集，产生了地形突变现象;图7(c)是在图7(b)的基础上利用高斯模型进行局部地形修正后的结果，房屋周围的地形突变现象得到了缓解，地形过渡自然。

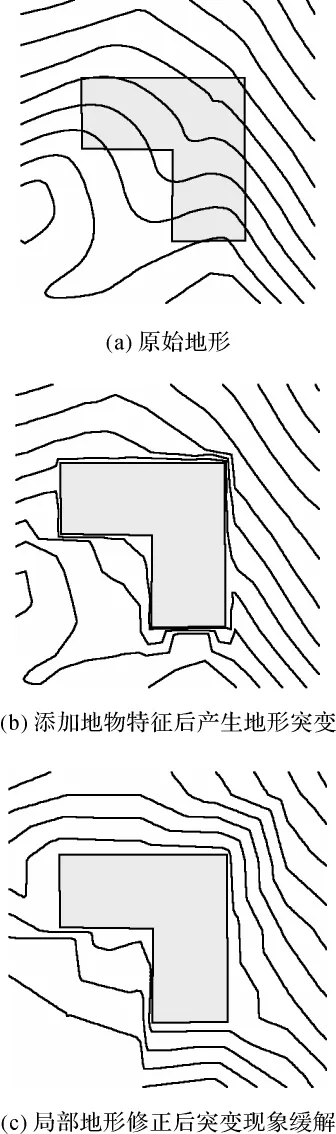
图7 实例验证结果

五、结束语

本文提出了一种改进的地物与地形匹配的方法，能够满足目视条件下对三维场景真实感和沉浸感的要求，并且具有一定的通用性。该方法较好地解决了面状地物(房屋、水体等)与地形的无缝匹配问题，并且在一定程度上解决了地形突变问题。匹配后的地形过渡自然，避免了部分地物与地形匹配过程方法中出现的“悬崖”和“台阶”现象发生。

［1］KERSTING O，DÖLLNER J.Interactive 3D Visualization of Vector Data in GIS［C］∥Proceedings of the 10th ACM International Symposium on Advances in Geographic Information Systems.USA：McLean，2002：107-112.

［2］宋汉辰，魏迎梅，吴玲达.三维对象模型与地形匹配的方法研究［J］.计算机辅助设计与图形学学报，2003，15(9)：1167-171.

［3］张辉，唐新明，吴侃.基于地理坐标框架下的地物与地形匹配解决方案研究［J］.测绘科学，2007，32(2)：90-92.

［4］刘宁，许敏.虚拟地形建模中的地物与地形匹配的算法研究［J］.测绘学院学报，2004，21(3)：215-218.

［5］王光霞，刘宁，万刚.虚拟地形环境中道路与地形模型融合算法研究及精度评价［J］.测绘学报，2005，34(4)：337-342.

［6］蒲浩，宋占峰，詹振炎.基于约束Delaunay三角剖分的道路三维建模方法［J］.华中科技大学学报：自然科学版，2005，33(6)：111-113.

［7］郑顺义，蒲浩，张祖勋，等.道路设计结果的三维实时动态浏览与漫游［J］.测绘通报，2004(7)：32-36.

［8］史文中.三维空间信息系统模型与算法［M］.北京：电子工业出版，2007.

［9］姚霄飞.基于Delaunay三角网的大比例尺地形改造［D］.郑州：信息工程大学.2008.

［10］康来.大规模 GIS数据三维可视化关键技术研究［D］.长沙：国防科学技术大学，2008.