T－1 型绝对重力仪的系统原理与测试结果

胡华，伍康，李刚，李哲，王力军

(中国计量科学研究院－清华大学精密测量联合实验室，清华大学精密仪器系，北京100084)

0 引言

精确的绝对重力值(g，常用值9.81 ms2)对大地测量、地球物理和精密计量具有十分重要的意义。通过重复观测绝对重力值以监测重力场的变化，可以为大地测量、地球物理、环境与灾害监测提供重要依据。近年来，重力测量在现代精密计量领域的地位日益突出，例如用于重新定义“千克”的瓦特功率天平实验，以及测定万有引力常数等。目前，由美国Micro －g 公司研制的一系列绝对重力仪在国际上占主导地位，其中性能水平最高的是FG5 型绝对重力仪［1－2］，测量不确定度达到微伽量级(1μGal = 10－8ms2)。

近年来，随着全球各国日益重视地学观测研究，许多国家的测绘、计量部门已采购FG5 型绝对重力仪，并将其作为绝对重力测量的“标准”仪器。2009 年9月，国际计量局在巴黎举办了第8 届国际绝对重力仪比对(该比对活动每4 年举行一次，主要目的在于确立国际重力计量的基标准和溯源体系，并检验不同的测量仪器之间是否存在较大的系统偏差)，共有来自全球各国的30 余台绝对重力仪参加，其中绝大部分是Micro－g 公司的系列产品，只有三台是自主研发的仪器，包括德国的MPG －2 型绝对重力仪［3］，意大利的IMGC－2 型绝对重力仪［4］，以及法国的原子干涉重力仪［5］。由于参加比对的仪器类型比较单一，使得潜在的系统误差难以被发现。因此，国际计量局明确表态，鼓励更多的基于不同原理和技术方案的新型绝对重力仪参加国际比对，以利于探索当前绝对重力测量领域尚未明确的系统测量误差［6－7］。

由于高精度绝对重力仪综合了精密机械、激光测量、时频测量、真空技术、隔振控制等多学科技术，自主研发难度较大。国内已有若干单位开展相关研究工作，但仍有一些关键技术问题较难突破，原理样机的总体性能水平不高［8－10］。除了采用经典的自由落体方案，国内也开展了基于原子干涉的绝对重力测量研究［11－12］，主要侧重于基础物理理论分析与实验验证，且原子干涉重力仪的系统复杂，体积庞大，距离实际应用还有较长的时间。

1995 年以来，国家测绘局、中国地震局、中科院测地所等单位先后引进了若干台FG5 型绝对重力仪，用于开展各自领域的高精度绝对重力测量任务［13－15］。然而，购买FG5 型绝对重力仪不仅价格昂贵(一台仪器约450 万人民币)，在仪器维修等方面存在许多问题和不便，重力测量数据的可靠性和溯源问题也无法保障。随着我国的“2000 国家重力基本网”和“中国地壳运动观测网络”的建成，对高精度绝对重力测量的需求日益增加［16］，全国只有数台FG5 型绝对重力仪远不能满足实际应用需求，迫切需要自主研制面向实际应用的高精度绝对重力仪，解决该类仪器只能高价进口导致的诸多问题。

近年来，清华大学在绝对重力测量的关键技术研究方面取得突破，自主研制完成T －1 型高精度绝对重力仪原理样机，主要面向实验室环境下的高精度绝对重力观测。2011 年以来，T－1 型绝对重力仪在国内若干重力测点进行了实验测试，均取得了微伽量级的高精度观测结果［17］。本文将简要介绍该仪器的系统原理和测试结果。

1 系统原理

T－1 型绝对重力仪采用自由落体方案，其基本原理是通过激光干涉测量技术，精确测量某物体在高真空度环境下的自由落体运动轨迹，根据测量所得的时间和位移数据，通过数学多项式拟合的方法，计算下落物体的运动加速度，即绝对重力加速度值。与现有的绝对重力仪相比，T －1 型绝对重力仪在多项关键技术方面进行了重大改进和创新。现有技术方案主要存在以下三方面的不足:

1)精密机械设计与运动控制技术，用于实现可重复的、稳定的自由落体运动。在现有的绝对重力仪中，真空腔内的下落物体被放置在一个支撑托盘上，支撑托盘固定在竖直方向安装的直线导轨的滑块上，支撑托盘和滑块可以沿导轨上下运动。支撑托盘通过机械传动系统，与真空腔外的马达传动系统连接。为了实现下落物体的自由落体运动，首先通过控制马达传动系统，将支撑托盘和放置在其上面的下落物体运送到真空腔的顶部位置;然后反向转动马达传动系统，使支撑托盘开始加速往下运动，其加速度略大于重力加速度，此时下落物体与支撑托盘分离，从而实现下落物体的自由落体运动。在真空腔的底部位置，通过控制马达传动系统，使支撑托盘减速运动，直至下落物体与支撑托盘接触，最后一起停留在真空腔的底部位置。因此，该马达传动系统可以重复实现下落物体的自由落体运动。

但是，现有的自由落体装置通过马达的高速转动来实现下落物体的自由落体运动，马达传动系统一直处于工作状态，导致自由落体装置在测量进行期间产生较强的振动，由于重力测量系统对于装置本身的振动非常敏感，因此这种系统会影响到重力测量结果的准确度。

2)激光干涉测量技术，用于精密测量下落物体的自由落体运动轨迹。通常采用改进型的马赫－泽德尔激光干涉测量装置，激光束进入干涉测量装置后通过分光镜，一部分激光作为测量光束，射向真空腔内的下落物体，下落物体内安装了回射棱镜，将测量光束反射回来;另一部分激光作为参考光束，射向一个放置在隔振平台上的回射棱镜，将参考光束反射回来。反射回来的测量光束和参考光束通过另一个分光镜实现合光，即可实现激光干涉测量，干涉条纹的数量与下落物体运动的位移成正比。在激光干涉测量装置中，需要精确调整测量光束的方向，使其与重力加速度方向即绝对竖直方向平行。

现有的激光干涉测量装置中，通常采用望远镜瞄准的方法来调整测量光束的竖直方向。但是，该方法需要使用多个光学器件和复杂的光路设计，这导致增加了系统的复杂度，并且容易产生操作误差。

3)高速信号采集与数据处理技术，用于处理激光干涉测量信号，通过特定算法得到重力加速度值。在现有的技术方案中，通常采用过零检测器和时间间隔分析仪获取激光干涉条纹信号的过零点特征。为了获取下落物体的自由落体运动特征，首先将激光干涉条纹信号通过一个过零检测器，检测干涉条纹信号的过零点;然后将过零点信号输入时间间隔分析仪，测量过零点之间的时间间隔。根据激光干涉测量原理，干涉条纹信号的两个相邻过零点对应着四分之一激光波长的运动位移，因此可以得到自由落体运动轨迹的时间和位移数据，通过进一步的数学多项式拟合，即可计算重力加速度的数值。

但是，现有技术方案中的过零检测器和时间间隔分析仪的电路系统可能引入非线性的相位噪声，这种利用硬件电路的方法获取激光干涉条纹信号的过零点特征，可能引入非线性的相位噪声，导致测量结果产生一定的偏差。

T－1 型绝对重力仪的设计综合考虑了以上现有技术方案的不足，提出并实现了若干关键技术的创新:

1)在T－1 型绝对重力仪中，通过采用弹性的下落构件悬挂方法，代替马达快速运转的传统方法，实现下落物体的自由落体运动，从而降低马达传动系统对自由落体装置的振动影响，提高重力测量的准确度。

2)在T－1 型绝对重力仪中，采用了新设计的小型化激光干涉测量装置，带有集成的光束垂直度精确调节功能，使得测量光束的校准更加简单精确，从而提高绝对重力测量的准确度，同时简化了系统结构以及操作步骤。

3)采用了新型的信号采集与处理技术，通过高速数据采集卡将激光干涉测量信号传输到计算机进行数字化处理，精确计算重力加速度数值，避免采用复杂的硬件电路进行信号处理，提高重力测量的准确度，简化了系统结构。

T－1 型绝对重力仪的主要组成部分如图1 所示，主要包括自由落体装置、激光干涉测量装置、隔振平台、信号采集与处理装置等。图2 中显示了绝对重力测量系统的具体结构图。

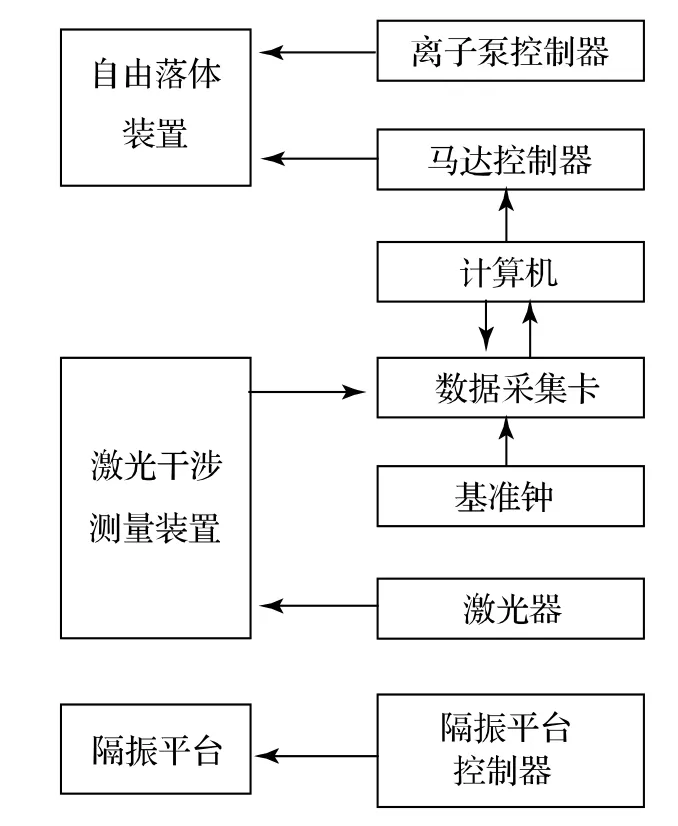
图1 绝对重力测量系统的主要组成部分

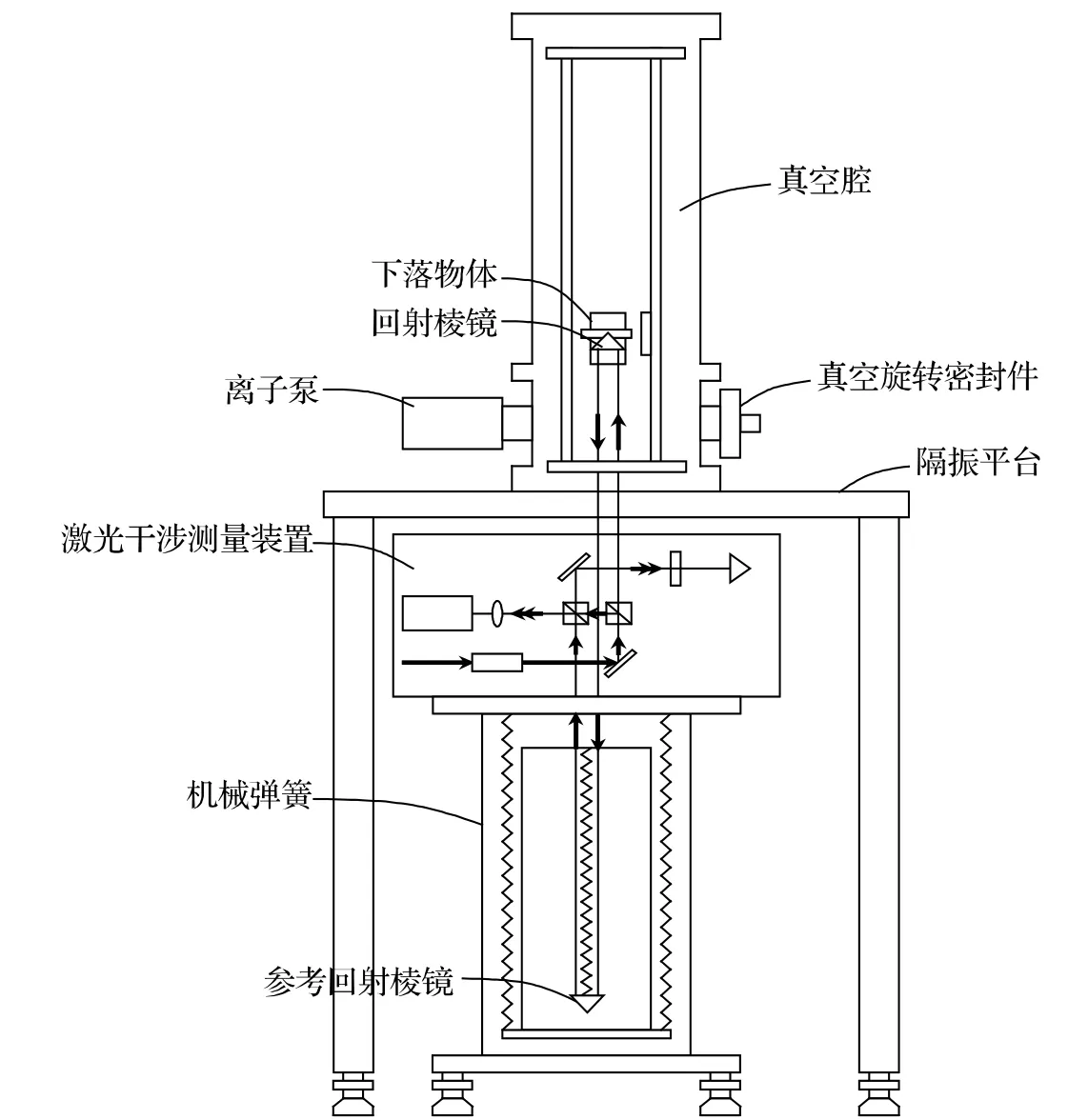
图2 绝对重力测量系统的具体结构图

自由落体装置用于实现物体的自由落体运动，其主要包括下述部件:真空腔;设置在真空腔内部的一系列机械运动装置，用于可重复的、稳定的实现下落物体的自由落体运动。在下落物体内部安装有回射棱镜，用于将来自激光干涉测量装置的测量光束反射回去。真空腔连接到离子泵，其用于保持真空腔内的高真空度，离子泵与真空腔之间通过标准的真空法兰连接，以保证连接的密封性。真空腔还设置有真空旋转密封件，其用于密封连接真空腔内的自由落体运动装置和真空腔外的马达。马达在外部计算机的控制下按一定的速度和方向转动，以控制下落物体的自由落体运动。

激光干涉测量装置用于测量下落物体作自由落体运动的位移，以计算其重力加速度值。该装置包括反射镜、分光镜、透镜和将激光干涉条纹转换为电信号的光电探测器等器件。激光干涉条纹信号反映了自由落体运动的位移、速度特征，该信号经过计算机软件算法处理，即可得到重力加速度的数值。激光干涉测量装置连接到一数据采集卡，其获取所述激光干涉条纹信号并传输给外部计算机进行处理。数据采集卡连接到铷原子钟，其为数据采集提供标准的时钟参考信号。

隔振平台设置在所述激光干涉测量装置和地之间，其用于隔离地面振动对测量的影响。如图2 所示，隔振平台中悬挂有参考回射棱镜，用于与激光干涉测量装置配合组成光路，将下落物体的回射棱镜反射的测量激光反射到激光干涉测量装置。此外，隔振平台还包括机械弹簧和精密控制系统。隔振平台通常可以实现超过20 s 的本征振荡周期，具有较好的隔离地面振动的效果。

2 测试结果

2011 年至今，T－1 型绝对重力仪在清华大学和中国计量科学研究院昌平重力精测实验室进行了多次重力观测，并参加了2011 年在卢森堡举行的欧洲绝对重力仪比对，均取得了微伽量级的高精度测量结果。

图3 是2012 年11 月T－1 型绝对重力仪在中国计量科学研究院昌平重力精测实验室的测量结果，测量结果的均值方差为0.4μCal。图中所示重力值已减去均值。采用分组测量，每组16 次下落，各组间隔30 min。图中的误差图标记为重力测量数据，实线为地球固体潮汐引起的重力变化理论曲线。误差图的高度为组内g 值测量结果均值的标准差，根据公式(1)计算。

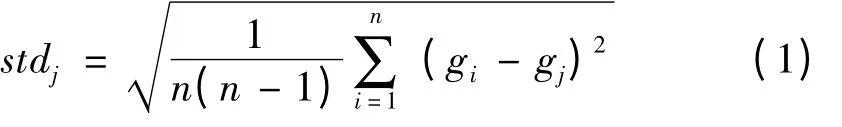
式中:n 为组内的g 值测量次数;gi为第i 次自由落体对应的g 值测量结果;gj为组内g 值测量结果均值(即组内所有gi的平均值)。

从图3 可以看出，各组内g 值测量结果的离散度极小，并且各组的测量结果与固体潮理论曲线具有很好的一致性。经固体潮修正后的g 值测量结果均值的标准差为0.4 μGal，已经达到优于微伽量级的精度。

图3 测量结果

2011 年11 月，T －1 型绝对重力仪前往卢森堡参加欧洲绝对重力仪比对任务，取得良好观测结果。共有来自全球各国的二十多台绝对重力仪参加此次比对，其中只有3 台仪器是自主研制的，包括T －1 型绝对重力仪，法国天文台的原子干涉重力仪CAG －01，以及意大利的上抛－下落式绝对重力仪IMGC －02。如图4所示，T－1 型绝对重力仪的测量结果与参考值相吻合，两者相差量在系统自评估的合成标准不确定度范围内(6μCal)，实际检验了仪器系统的可靠性和测量准确度［18］。值得注意的是，在本次比对中，不同的FG5 型绝对重力仪之间的测值差异最大可达到10μCal以上(FG5 －233 与FG5 －102)，这表明现有的重力测量仪器可能存在较大的尚未探明的系统误差，仍需进一步研究分析。

图4 2011 年欧洲绝对重力仪比对结果

3 结论与展望

T－1 型绝对重力仪为自主研制的高精度、可搬运式绝对重力测量装置，采用新型的自由落体装置、激光干涉测量技术和信号处理技术，可实现微伽量级不确定度的精密重力测量。经过进一步改进与工程化设计，该仪器有望在国内多个领域发挥重要应用。特别是在力学领域，高精度绝对重力仪能够满足国内测力、测压、扭矩等元器件及仪器仪表生产商对精确重力测量的要求。

［1］Faller J E. Thirty years of progress in absolute gravimetry:a scientific capability implemented by technological advances［J］.Metrologia，2002，39，425 －8.［2］Niebauer T M，Sasagawa G S，Faller J E，et al. A new generation of absolute gravimeters［J］. Metrologia，1995，32，159 －80.

［3］Hu H，Svitlov S，Rothleitner C，et al. Improvements of the MPG － 2 transportable absolute ballistic gravimeter ［J］ .Metrologia，2010，47，575 －582.

［4］D’Agostino G，Desogus S，Germak A，et al. The new IMGC－02 transportable absolute gravimeter:measurement apparatus and applications in geophysics and volcanology［J］. Annals of Geophysics，2008，51 (1)，39 －49.

［5］Bodart Q，Merlet S，Malossi N，et al. A cold atom pyramidal gravimeter with a single laser beam［J］. Applied Physics Letters，2010，96，134101.

［6］Jiang Z，Pálinká? V，Arias F E. The 8th International Comparison of Absolute Gravimeters 2009:the first Key Comparison(CCM.G－K1)in the field of absolute gravimetry. Metrologia，2012，49，666 －684.

［7］ Jiang Z，Francis O，Vitushkin L. Final report on the Seventh International Comparison of Absolute Gravimeters (ICAG 2005)［J］. Metrologia，2011，48，246 －260.

［8］吴书清，吉望西，刘达伦，等. 重力仪数值计算及不确定度评定方法［J］.. 计量学报，2009，30 (3)，212 －215.

［9］张为民，王勇，周旭华. 我国绝对重力观测技术应用研究与展望［J］. 地球物理学进展，2008，23 (1)，69 －72.

［10］吴琼，郭有光，滕云田，等. 重力仪设计中的一种新型落体控制方式［J］. 地球物理学进展，2011，4 (2)，443 －449.

［11］Zhou L，Xiong Z Y，Yang W，et al. Measurement of local gravity via a cold atom interferometer ［J］ . Chin. Phys.Lett.，2011，28 (1)，013701.

［12］Zhou M K，Hu Z K，Duan X C，et al. Performance of a coldatom gravimeter with an active vibration isolator［J］. Physical Review A，2012，86，43630.

［13］邢乐林，刘冬至，李建成，等. FG5 绝对重力仪观测比对［J］. 测绘信息与工程，2008，33 (1)，25 －27.

［14］刘冬至，邢乐林，徐如刚，等. FG5 /232 绝对重力仪的试验观测结果［J］. 大地测量与地球动力学，2007，27(2)，114 －118.

［15］张为民，王勇，詹金刚，等. 1996 －2003 年中国大陆高精度绝对重力观测［J］. 地球物理学进展，2005，20 (1)，204 －210.

［16］张为民，王勇，詹金刚，等. 中国地壳运动观测网络中的绝对重力测定［J］. 武汉大学学报，2004，29 (3)，227－230.

［17］胡华，伍康，申磊，等. 新型高精度绝对重力仪［J］. 物理学报，2012，61，099101 －1 －8.

［18］Francis O，Klein G，Baumann H，et al. Final report of the regional key comparison EURAMET.M.G－K1:European Comparison of Absolute Gravimeters ECAG － 2011. Metrologia，2012，49 (1A)，07014.