引信头锥摆动角对火箭弹气动特性及控制能力影响*

王朋飞，曹红松，刘务平，刘 莎，解宁波，沈冠军

(1中北大学机电工程学院，太原 030051;2国营791厂，重庆 401336)

0 引言

为了提高现有库存尾翼火箭弹的打击精度和杀伤效能，在无控火箭弹上加装简易的制导和控制组件转换成弹道修正火箭弹，实现精确打击的能力，已成为各国发展的主要方向。实现二维弹道修正采用的修正执行机构主要有微型脉冲推力火箭、燃气射流控制发动机和空气动力鸭舵。前一种现已经成功应用于精确制导弹药上，但其结构复杂，只能提供次数有限、推力恒定的离散式修正，而且受空间尺寸的限制很难在引信上使用;后一种在修正弹上也已得到应用，但在二维弹道修正引信方面的应用还不成熟[1]。

引信头锥摆动火箭弹通过电机驱动引信摆动，从而为火箭弹弹道修正提供所需的气动力和力矩，这种方法可以大批量改造现有库存火箭弹的射击精度[1]。文中通过方便、有效的仿真软件Flow simulation对引信头锥摆动火箭弹进行外流场气动仿真，分析了引信摆动角对火箭弹的气动特性的影响;并利用仿真得到的气动参数对火箭弹二维修正能力进行了仿真研究。

1 引信头锥摆动时火箭弹的受力分析

相对于常规火箭弹，引信头锥摆动火箭弹将产生附加的气动力和力矩，受力如图1所示。图中α为攻角，α1为引信头锥摆动角，Rx、Ry、Mz为火箭弹攻角引起的气动阻力、升力、俯仰力矩，Mω为俯仰阻尼力矩，Rx1、Ry1、Mz1为由引信头锥摆动角引起的附加气动阻力、升力、俯仰力矩[2]。

图1 引信头锥摆动时火箭弹的受力图

2 外流场仿真模型建立

2.1 火箭弹外流场仿真模型

利用Solidworks软件中的Flow simulation插件进行外流场分析。仿真模型为直径d=122mm的低旋火箭弹，全长为 23.68d，弹头部长为3.1d，弹头部与圆柱部通过卡门曲线连接，头部为半球形。为了能够更加准确的模拟流场，消除流场区域边界的干扰现象，建立的流场区域为一个长为15d，宽高为20d的长方体。为了提高仿真的精度和减小仿真时间，对弹体周围的网格进行细化，外部由较稀疏的网格构成。计算区域的纵向对称平面的网格模型如图2。

图2 纵向对称平面弹体周围的网格模型

仿真条件:Flow simulation采用离散与时间相关的Navier-Stokes方程组，并基于计算网格来求解该方程组[3]，采用默认的湍流模型，材料选择理想气体模型，弹体壁面条件选为绝热，对所要得到的参数(阻力系数、升力系数和俯仰力矩系数)进行选取并将其解算值的收敛作为仿真结束的条件。

2.2 外流场力学模型

流体流动要受物理守恒定律的支配，基本的守恒定律包括:质量守恒定律、动量守恒定律、能量守恒定律。流体动力学控制方程就是这些守恒定律的数学描述[4]。

1)质量守恒方程

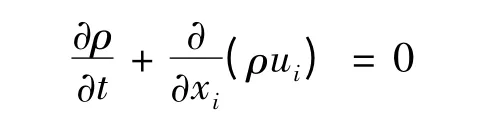
质量方程又称连续方程，该方程是质量守恒方程的一般形式，它适用于可压流动和不可压流动。

2)动量守恒方程

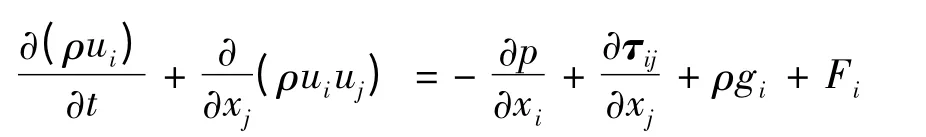
动量守恒方程又叫运动方程，式中p是静压，τij为应力张量，ρgi和Fi分别为i方向上的重力体积力和外部体积力。

3)能量守恒方程

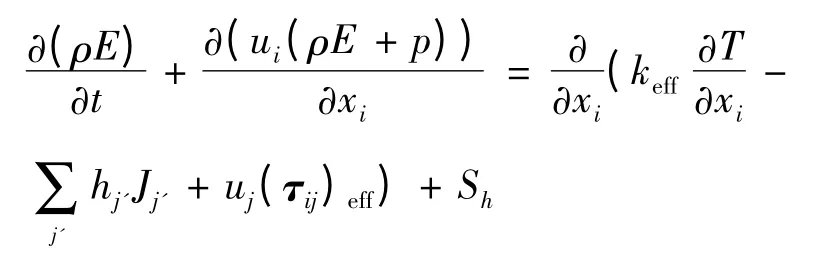
式中:keff是有效热传导系数;Jj'是组分j'的扩散流量。

2.3 模型的验证

图3是火箭弹被动段无引信头锥摆动角和攻角时阻力系数仿真结果与工程算法(该方法已经很成熟)得到的数据对比图。由图可知，仿真结果与工程算法所得到的数据在各个马赫数下整体吻合较好，在1.8Ma到2.5Ma相差较大，但最大误差不超过11%，表明仿真结果是可信的。

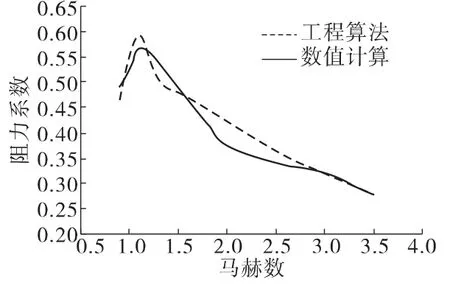
图3 阻力系数对比

3 摆动角对气动特性的影响

3.1 摆动角对头部流场特性的影响

图4、图5分别为Ma=1.5，引信头锥摆动角为8°时，纵向对称平面上的压力和密度等势线图。由图可知，引信头锥摆动角引起火箭弹头部上下区域流场不对称，下表面区域附近的压力、密度明显比上表面区域附近高[5]，这种不对称使火箭弹头部产生一个附加气动力，此气动力对火箭弹质心将产生气动力矩。因此，可通过控制引信头锥摆动角的大小和方向，调整火箭弹的飞行姿态，实现火箭弹的二维弹道修正。

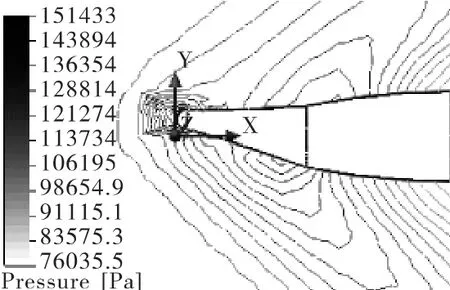
图4 摆动角为8°时的压力等势线图

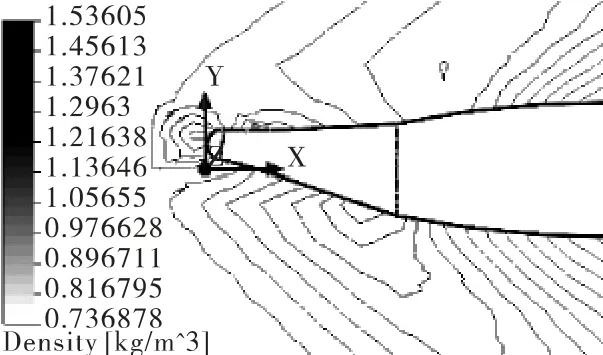
图5 摆动角为8°时的密度等势线图

3.2 摆动角对气动参数的影响

针对火箭弹在0°攻角，引信头锥摆动角为0°、4°、8°、12°时仿真得到的全弹阻力系数、升力系数和俯仰力矩系数随马赫数的变化曲线，如图6～图8。

由图6知，跨音速段，在同一马赫数下，全弹阻力系数随引信头锥摆动角的变化不明显;超音速段，全弹阻力系数随引信头锥摆动角的增大有较小的增加，这是由于在超音速飞行的火箭弹将产生激波阻力，引信头锥摆动角越大产生的激波阻力也越大。

由图7、图8知，在相同马赫数下，升力系数和俯仰力矩系数随引信头锥摆动角的增大都有显著增加，且幅度也越大。

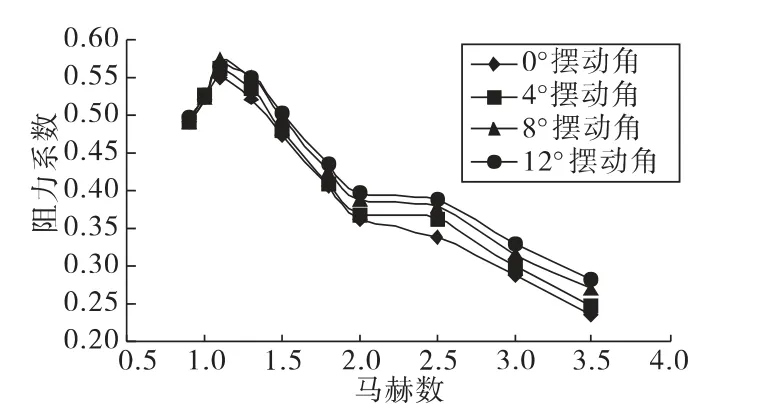
图6 阻力系数随摆动角变化曲线

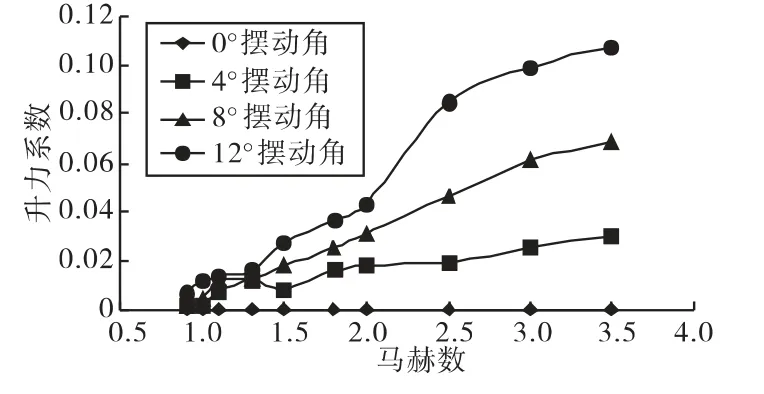
图7 升力系数随摆动角变化曲线

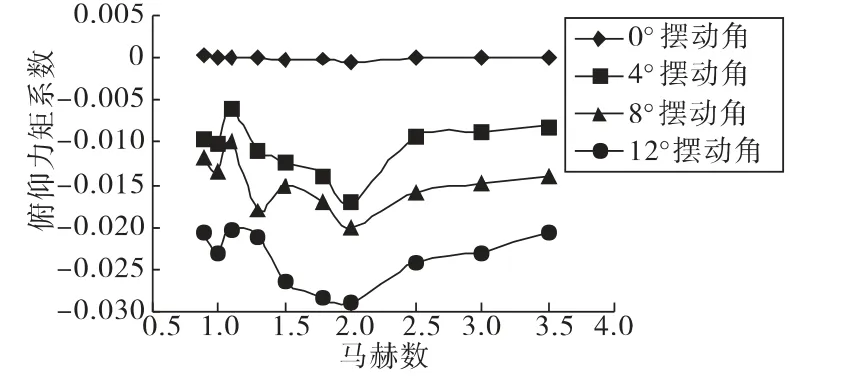
图8 俯仰力矩系数随摆动角变化曲线

4 控制能力分析

火箭弹散布一般较大，对于射程为40km的火箭弹，要求横向和纵向的修正距离约为1300m、1000m。无控时火箭弹的弹道参数如下:射角55°，初始转速31.4rad/s，射程 40210.3m，飞行时间 122.01s，弹道顶点时间 55.21s。

图9 纵、横向修正距离随摆动角的变换曲线

图10 射程－飞行高度随摆动角变化曲线

假设过弹道顶点后(56s)起控，射角为55°条件下，纵向和横向修正距离随引信头锥摆动角的变化曲线如图9所示。过弹道顶点后，射程－飞行高度随引信头锥摆动角变化曲线如图10所示。

由图9、图10可知，纵向和横向修正距离随引信头锥摆动角(绝对值)的增大而增大。横向向左向右的修正距离基本相等，纵向向前的修正距离明显比向后的修正距离少。

纵向修正时，8°、12°摆动角下攻角随时间的变化曲线如图11、图12。由图知，火箭弹的攻角在初始位置和起控位置都出现了波动，初始位置的波动主要是由起始扰动引起的，起控位置的波动是由于引信头锥摆动角改变了火箭弹的整体外形，引起全弹攻角的变化，且摆动角越大起控位置攻角变化越大，影响火箭弹的稳定性飞行。因此，在满足修正能力的前提下，要减小引信头锥摆动角的度数对稳定性飞行的影响。

图11 摆动角为8°时，攻角随时间变化曲线

图12 摆动角为12°时，攻角随时间变化曲线

5 结论

仿真结果表明，引信头锥摆动角的存在，引起火箭弹头部在纵向对称平面内下区域流场的压力、密度明显大于上区域流场，产生附加的升力和俯仰力矩，并使全弹的升力系数和俯仰力矩系数随着引信头锥摆动角的增大而显著增加;外弹道仿真表明，引信头锥摆动角所提供的气动力和力矩通过对火箭弹姿态的控制，可以进行二维弹道修正，并能达到横向和纵向的修正要求，仿真结果对改进弹道修正火箭弹设计能起到参考作用。

[1]王梦龙，王华，韩晶.基于引信头锥摆动的火箭弹弹道修正方法[J].探测与控制学报，2011，33(4):23 －25.

[2]魏方海，王志军，吴国东.控制火箭弹头部偏角的弹道修正技术[J].弹箭与制导学报，2006，26(2):928－930.

[3]DS Solidworks Company.Solidworks Flow Simulation 教程[M].杭州新迪数字工程系统公司，译.北京:机械工业出版社，2011.

[4]王福军.计算流体动力学分析——CFD软件原理与应用[M].北京:清华大学出社，2004.

[5]Guo Jianguo，He Yuanjun，Zhou jun.Modeling and simulation research of missile with deflectable nose[C]//Intellgent Computing and Intelligent Systems，ICIS2009，IEEE International Conference，2009:86－88.