生产率、资本回报率和增长率的良性互动——“中国奇迹”的一种新解释

陈培钦，华中科技大学 经济学院，湖北 武汉430074

引 言

改革以来，中国经济高速发展，取得了举世瞩目的成就。国民生产总值年均增长率达到9．9%，造就了“中国奇迹”。现有文献主要从制度变迁和人力资本等角度对“中国奇迹”进行解释［1］［2］29-48［3］5-25，而对于资本形成的重要性认识不足。甚至有一些学者认为，中国这种主要靠要素投入的增长模式是不可持续的，是“纸老虎”，最终经济增长将从“奥林匹亚山的神殿拉回到德塞利平原上”［4］641-680，故从这一角度而言，所谓的“中国奇迹”，是一种粗放型的增长，只是短暂的繁荣，而非一个长期的成功模式［5］1220-1261［6］12-23［7］190-197。

然而，这一观点依赖于两个隐含的假定，一是我国的高投资缺乏微观基础，二是高投资必然导致粗放型的增长。但是，根据Bai 和CCER的测算，我国的资本回报率并不低，因而我国的高投资是有其合理的微观基础的［8］61-88［9］723-758;并且，改革以来我国的生产率呈现不断增长的趋势［10］3-10［11］339-351［12］32-39，甚至 有学者 的测算 表明TFP 的年均增长达到6．8%［10］，因此也没有理由认为“中国奇迹”就是粗放型的增长。

特别是，根据“干中学”模型，资本形成可以通过边干边学提高生产率水平，而生产率水平的提升又会促进经济增长，从而依靠要素投入的增长是可以持续的［13］155-173［14］。那么，如果“干中学”效应在我国存在，则是否存在这样一种机制解释“中国奇迹”，即高的生产率和增长率促进了我国的资本回报率上升［15］15-21［16］47-54，导致较高的投资［17］3-24，而高投资一方面通过“干中学”效应，促进了我国生产率的上升，另一方面直接导致了经济的快速增长［18］［19］1-14［20］777-808［21］432-452［22］141-174。另外，生产率的提高和GDP 的上升又是相互促进的:一方面，生产率的增加是经济长期增长的最重要驱动［23］312-320;另一方面，GDP 增长带来的需求规模的扩张可以带动生产率的提升。这是因为，需求扩张使市场规模扩大，进一步导致创新加快，采用更先进的技术，促进生产率提高［24］1049-1090［25］［26］44-56;同时，市场规模扩大导致竞争加剧，企业间的优胜劣汰使得资源更加有效地配置，从而提高生产率［27］1181-1222［28］295-316。这些因素的相互作用如图1 所示:

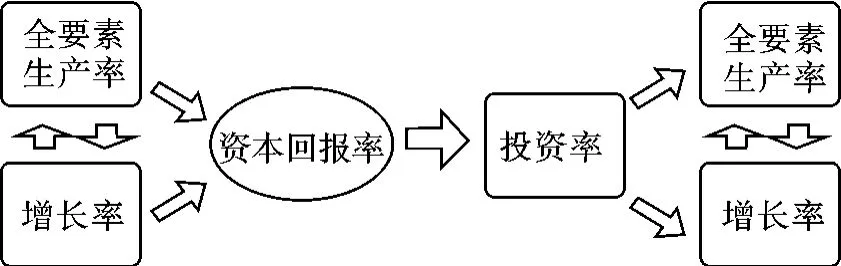
图1 生产率、增长率、利润率、投资率的相互作用

如果图1 所描述的是正确的、真实的，那么就为改革以来的“中国奇迹”提供了一个从资本回报率方面分析的新视角。特别是，在图1 所描述的这样一种增长方式下，中国经济的增长不仅是可持续的，而且进入了一种良性循环，实现百年复兴之梦是可以期待的。

注意到，如上文所述，对于上述猜想的各个主要环节，已经分别有文献进行了证实，而“干中学”效应和生产率的增长，在Romer 提出理论模型后，虽然影响巨大，但实证研究不多①据笔者所知，只有少数文献考察了干中学和生产率的关系，如刘细良、苏艳(2007)、傅东平(2009)、余官胜(2009)。，并且也缺乏文献对上述“中国模式”予以把握和说明。有鉴于此，本文将采用面板向量自回归(PVAR)的方法对上述猜想进行论证。我们认为，采用该方法具有以下几个优点。

第一，系统地考察了生产率、增长率、资本回报率和投资率四者的关系。这四个变量对于一国的增长无疑都有非常重要的意义，特别对于中国，投资率有着更为重要的作用。然而，在以往的研究中，往往只涉及其中某一方面，而缺乏一个系统的研究。通过利用PVAR 方法，我们得以将这四个变量放在一个模型中，进而考察其相互关系，并从资本回报率的视角对我国的增长之谜进行一个全新的解读。

第二，由于这四个变量之间相互作用的关系较为复杂，往往两个变量之间有着互为因果的关系，如生产率和增长率之间可能存在相互促进的关系，因而传统研究中依靠回归分析的方法可能会因为存在内生性而造成不一致的估计结果，影响结论的可靠性。并且，传统的回归方法难以将变量之间的相互联系区分开，特别是当几个变量之间存在非线性关系的时候。而PVAR 方法不需要事前对各个变量之间的因果关系进行假定，从而克服了以往研究的缺点。进一步，可以利用面板Granger 因果关系检验对各个变量之间的因果关系进行一个大致的推断;可以利用正交化脉冲响应函数将这各个变量的效果完全区分，借以考察当其他变量不变的情况下，一个变量对另一个变量冲击的反应。

第三，在现有文献的基础上，进一步证实生产率和增长率对资本回报率的促进作用。已有部分文献证实了这两者对资本回报率的提升作用，但是，这类文献非常之少，并且这些文献基本是一种静态的视角，如黄伟力利用简单的时间序列数据［15］15-21，黄先海等用一个生产函数的分解框架进行了论证［16］47-54。本文利用PVAR 方法，从动态的视角进一步发现了生产率和增长率确实对资本回报率有正向作用，从而进一步丰富了已有文献。

第四，如前文所述，自从Romer 提出“干中学”模型后，尽管其理论影响很大，但相对缺乏系统的中国经验的研究。本文的研究试图弥补这一缺陷。

本文的余下部分安排如下:第一部分说明“干中学”效应和PVAR 方法的模型，以及相应的估计方法和数据处理;第二部分介绍经验结果;第三部分进一步考虑在加入资源品价格变化之后对模型结论的影响;最后进行总结。

一、模型、方法和数据

1．“干中学”效应

在新古典增长理论的框架中，长期人均收入的增长取决于外生的生产率。这样一来，“增长模型最重要的决定因素居然不包含在模型之中，显然是不能令人满意的”［29］，于是，Romer 基于Arrow 的思想提出了将生产率进步内生化的干中学模型［14］。其基本思想是，在生产活动中，人们会不断考虑改进生产的方式和流程，从而创造出新方法，获得生产率的提升。因此，生产率的进步不是有意研发的产物，而是资本积累的一个副产品。并且，个人在生产过程中获得的知识，会通过外溢作用导致整体经济生产率水平的提升。具体的，考虑如下的简单情形:

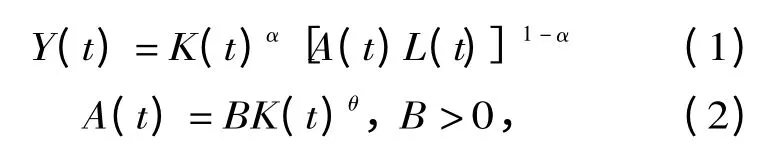
其中，Y、K、L分别代表总产出、资本和劳动，A表示“知识”或者生产率，B和θ 是参数。从上面两个方程中可以看出，投资行为或者资本积累的过程，不但增加当期的产出，还会通过“干中学”效应获得副产品，即生产率的提高。从这一角度而言，高投资和高积累未必是洪水猛兽，单纯依靠投资也能实现经济的长期增长。

2．面板向量自回归模型和估计方法

在接下来的分析中，本文使用面板向量自回归方法。对应于每一个省份i和时间t，模型如下:

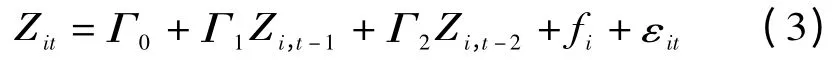
其中，Zit为一个五变量的向量Zit=(ktl，tfp，cr，itk，g);ktl表示资本劳动比，用来度量资本深化程度，放在模型中是作为影响资本回报率因素的一个控制变量;tfp表示全要素生产率的进步;cr表示资本回报率;itk代表投资对资本存量的比例，这样处理的原因是由于各省份经济规模相差很大，投资的规模相差也很大，这里参考文献的做法，将投资利用资本存量数据进行处理［30］190-210［31］313-350;而最后一个变量g代表增长率。也就是说，在上述模型(3)中，我们考虑了影响资本回报率的几个最为重要的因素，即生产率、增长率、投资率和资本深化程度。

考虑到不同省份具有特异性，而这一特异性可能和滞后的解释变量Zi，t-1相关，导致系数估计偏误，我们在模型中加入了允许异质性的个体效应fi。由于方程含有被解释变量的滞后项，无法简单进行组内均值差分，我们采用Helmert 方法进行处理［32］29-51。该方法只去除每一个变量的前向均值，可以有效地避免固定效应偏误。对于处理后的方程，我们采用系统GMM 的方法进行估计。

在接下来的分析中，由于我们要用到正交化脉冲响应函数，因而向量Zit中变量的顺序是重要的①这是因为，脉冲响应函数描述的是，当其他冲击(shock)保持不变时，系统中其他变量对该系统中某一个变量的革新(innovation)的反应。然而，由于在我们的模型中，生产率、增长率、利润率、投资率等变量有着千丝万缕的联系，因而很难保持其他变量的冲击不变，也就是说，残差向量的方差协方差矩阵不是正交(orthogonal)的。为了解决这一问题，需要借助乔里斯基分解(Choleski decomposition)将残差的方差协方差矩阵变成阶梯形的。但是，这一分解过程对变量进入模型的顺序不是中性的。事实上，该分解方法倾向于将两个变量的相关部分归结给首先进入模型的变量，因此，设置变量进入模型的顺序是重要的。参见Hamilton(1994)和David C．Lay(2010)。。一般而言，外生的变量应该首先进入模型。就我们分析的目的而言，资本劳动比仅仅是作为资本回报率的控制变量，因而最先放入模型;现代经济周期理论一般认为，外在冲击主要来源于生产率的冲击［33］，因此，生产率放在第二位。由于生产率的变动会影响资本回报率，所以资本回报率第三位进入模型。资本回报率变动导致投资率变动，投资率的变动进一步影响了增长率，因此这两个变量依次在第四、第五位进入模型②可能有人会提出质疑，即经济增长率是否应该在生产率之后就进入模型，原因是上文中图1 表明，生产率的提高会引起增长率上升，而增长率导致资本回报率的提高。但是，我们认为，在我国的背景下，GDP 的增长率更多的是投资带来的，因此将增长率放在后面。并且，一般来说，生产率冲击产生之后，投资作为一个最具波动性的变量，一般反应先于增长率。。

3．指标选取和数据来源

上述指标中，增长率g的度量采用不变价GDP 的对数取差分得到，即gt=lnGDPt-lnGDPt-1，其中，GDP 的平减指数采用司春林等的方法算出［34］46-54。资本回报率的计算，借鉴大多数文献的做法，基于Bai 的方法计算［8］，其公式为:

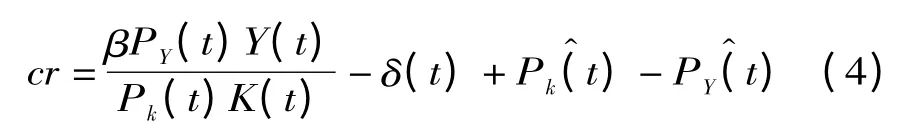
(4)式中，cr为资本回报率，Y(t)和K(t)表示第t期的实际产出和资本存量，δ(t)表示折旧率，β为产出中的资本份额，而Pk(t)-PY(t)代表资本品价格相对于产成品价格的变动。(4)式中的分子可以看成是资本品投入所带来的收入，而分母则表示资本的现价存量。我们发现，改革以来，我国各省资本品价格和产成品价格波动差异较大，为了避免资本品价格和产成品价格剧烈波动对资本回报率估算结果的影响，在实际计算中，我们不考虑资本品价格相对于产成品价格变动的部分(这部分可以对应于财务管理中的“资本利得”)。另外，在Bai的计算中，资本收入份额的计算采用的是收入法GDP中扣除劳动者收入的部分，也就是说，将生产税净额全部计入资本收入［8］。但是，近年来研究劳动份额的文献指出，生产税净额是在劳动和资本之间的“楔子”，政府对资本征收的生产税会转嫁到劳动者身上。因此，在计算资本份额时，我们依照Gamme 和Rupert 的观点将生产税净额在资本和劳动之间进行了分配［35］92-105。另外，注意到我国在2004年和2009年对收入法GDP 中劳动者报酬的统计口径发生了两次调整，我们依照周明海等的方法对其进行了处理，从而获得的资本回报率数据是前后一致可比的［36］35-45。

生产率的度量方面，以往的文献多采用基于Malmquist 指数的DEA 方法或者Battese 等提出的方法进行测度。然而，前者没有考虑产出中随机扰动的部分，而后者没有考虑到各个产出单元中的固定效应对产出的影响，因而受到 了 Greene 以 及 Wang 和 Ho 的 批评［37］7-32［38］286-296。本文采用基于固定效应的面板随机前沿模型估计生产率中的技术效率①该估计采用王泓仁教授提供的stata 程序实现。在生产函数方程的估计中，我们采用超越对数生产函数进行估计，考虑了劳动和资本两个投入。在无效率方程的估计中，我们借鉴已有文献的做法，考虑了出口占GDP 的比重、政府支出占GDP 的比重、国有企业比重和第一产业比重四个指标作为影响无效率项的变量。具体的估计结果由于篇幅限制不再列出，有兴趣的读者可以向作者索要。，从而解决了以往估计方法中没有考虑固定效应参数导致的偏误问题。

本文的所有数据均来自新中国六十年统计资料汇编和各省的统计年鉴，其中，资本存量和资本品价格指数的数据采用单豪杰的数据［39］17-31，并按其方法进行了补充。考虑到数据的可得性和连续性，参考多数文献的做法，将重庆并入四川，将海南和西藏从样本中删除，最终进行分析的是28 个省市1978-2010年的资料。

二、经验结果分析

1．PVAR 估计

由于PVAR 要求模型中的变量都是平稳的，因此在正式分析之前，首先要进行数据的平稳性检验。这里分别利用五种不同的面板单位根检验，检验的结果如表1 所示。

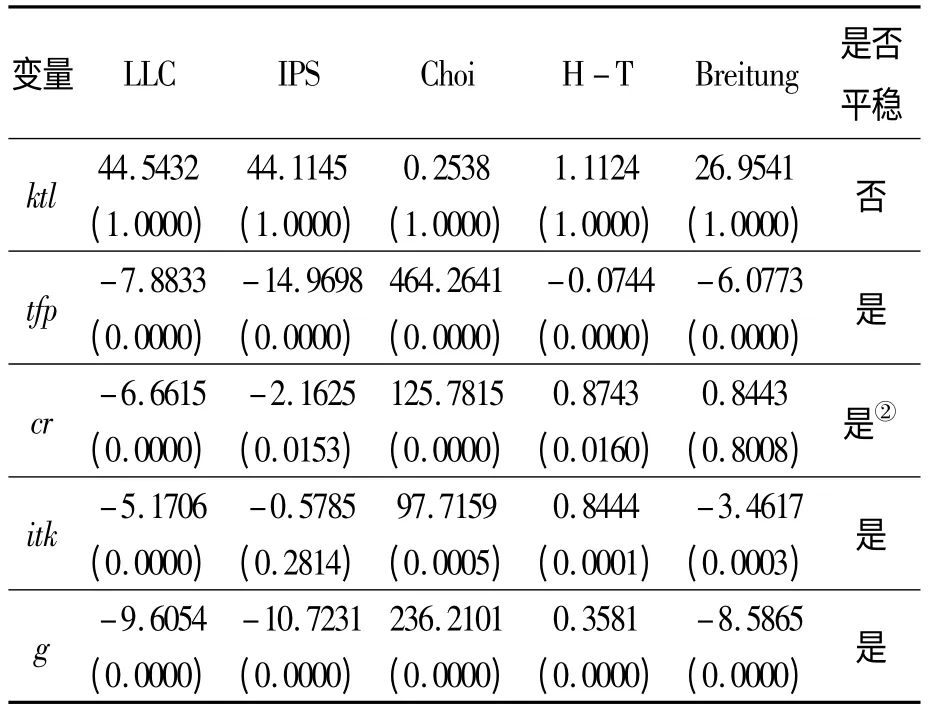
表1 面板数据的单位根检验

从表1 中可以发现，除了人均资本存量ktl是不平稳的外，其他变量都是平稳的。由于经济变量大多是I(1)过程，因而在下面分析中，我们将ktl取一阶差分③差分后的变量经过多变量ADF 检验发现是平稳的。。

表2 滞后阶数的选取

关于滞后阶数的选取，如表2 所示，BIC 建议选用2 阶滞后，而AIC 和HQIC 建议选用4阶滞后。由于我们的变量较多，如果采用4 阶滞后，需要估计的参数过多(有55 个参数)，可能会降低估计结果的准确性。另一方面，AIC和HQIC 倾向于选择一个较为“丰满”的模型，而BIC 对增加解释变量的惩罚更严厉，选择的模型比较精简。综合上述因素考虑，我们选择2 阶滞后模型，估计的结果如表3 所示。

表3 PVAR 估计结果

2．脉冲响应函数分析

由于VAR 估计是乏理论(Atheoretic)的，所以对于模型的参数估计值，通常并不分析其经济意义。因此，我们对于上述估计结果也不进行过多的分析，而是转为考虑脉冲响应函数。脉冲响应函数反映的是某一变量的一单位革新(innovation)对模型中其他变量的影响。就我们的目的而言，分析脉冲响应函数需要估计其置信区间。这里置信区间的构造方法是采用Monte Carlo 模拟方法①具体的构造方法参见Love and Zicchino(2006)，这里为了结果的稳健性，将蒙特卡洛模拟进行了2 000次。，脉冲响应函数的结果如图2 所示。

我们发现，正交化脉冲响应函数的估计结果很好的证实了本文开头提出的假说。从图中可以看出，第一，我国生产率和增长率的进步促进了我国的资本回报率提高。生产率的一单位冲击在第一期对资本回报率有一个显著的正向影响，并且该效果持续的时间较长，一直到第4期以后才开始不显著。增长率的冲击对资本回报率也有正向的影响，虽然持续的时间较生产率略短。考虑到改革以来我国增长率和生产率保持了非常快的进步，因而增长率和生产率是促进我国资本回报率提升的重要因素。

第二，资本回报率的提高可以显著促进投资的增加。图2 中资本回报率的一单位正向冲击对投资有着长期的持续正向影响，且该影响一直到6 期仍然显著异于零，且有扩大的趋势。这说明我国的投资对利润率的变动还是较为敏感的。同时，我国的高投资很大程度上是受资本回报率驱使的，投资是有其微观基础的，高投资是否一定低效率仍需要进一步的研究。

第三，我国的投资具有一定的“干中学”效应，高投资可以导致生产率的提高。从图2 中可以看出，投资的一单位冲击可以导致生产率在前两期产生一个正向的变动，这说明投资能在一定程度上促进知识的习得，从而是有利于生产率的。虽然我们的结果表明这一“干中学”效应较小，并且持续的时间也不长，但考虑到我国投资规模很大，因此这一效应还是很可观的。

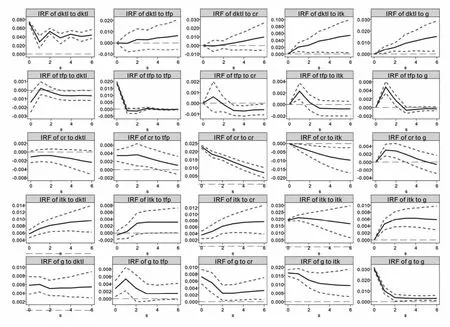
图2 生产率、利润率、投资率和增长率的相互作用

第四，生产率和增长率之间具有相互促进作用。生产率促进增长率的提高已是学界共识，而增长率对生产率的拉动作用，与上文中提到的从需求角度研究生产率的文献结果一致。从直接效应上看，需求规模的扩张，一方面导致要素的使用效率提高，另一方面导致企业扩大生产规模，从而有助于规模经济的发挥;再者，需求的扩张导致更多的投资进入市场，导致竞争加剧，加速优胜劣汰，从而可以导致生产率的提升。从间接效应看，需求规模的扩大会导致研发支出扩张、人力资本投资增加，并且影响国际技术溢出，从而提升全要素生产率［40］。

上述分析表明，引言中关于“中国奇迹”原因的猜想，即生产率、利润率、投资率、增长率相互作用的模式是存在的。但是，脉冲响应函数只能说明每一个变量对冲击的反应，并不能说明变量之间的先后关系。为了对上述问题进行进一步考察，我们考虑格兰杰因果关系检验，其结果如表4 所示。

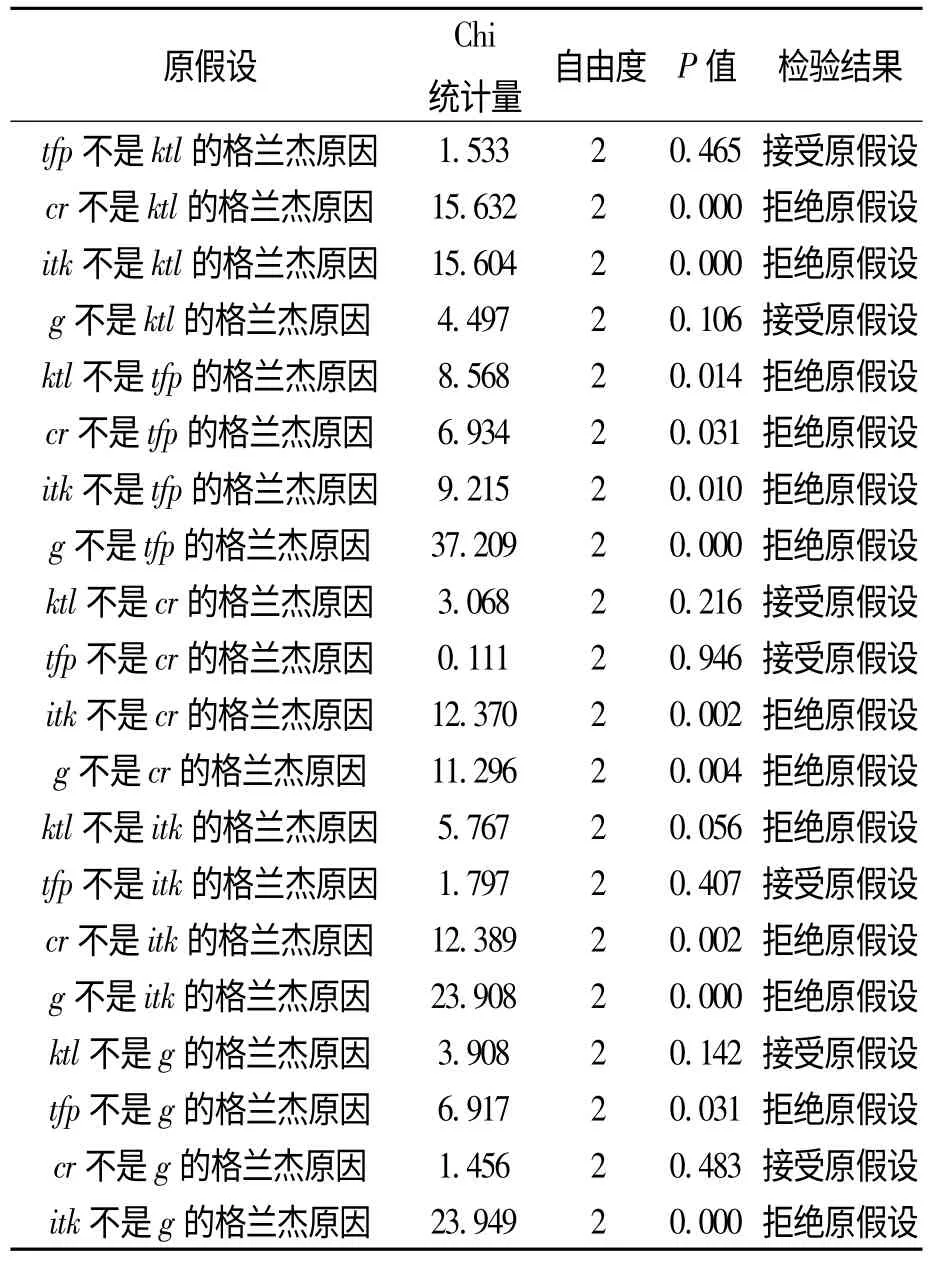
表4 格兰杰因果关系检验

从表4 中可以发现，增长率和生产率互为格兰杰因果关系，这说明了图1 中第一步的关系是存在的。另外，利润率构成了投资率的格兰杰原因，这说明图1 中第三步的关系也是成立的。进一步，投资率构成了生产率和增长率的格兰杰原因，这说明了图1 中第四步关系是正确的。也就是，投资在很大程度上直接促进了国民收入的增长，又在一定程度上通过“干中学”效应提升了生产率水平。

这里有一个和前面脉冲响应分析不一致的地方就是，虽然发现增长率构成了我国资本回报率的格兰杰原因，但是生产率是资本回报率格兰杰原因的假定却没有得到数据的支持，但是，考虑到已有的文献都证明了生产率对资本回报率有显著影响［15］15-21［16］47-54，因此我们仍认为这一关系是成立的。

三、考虑了资源品价格后的经验结果

在上面的分析中，我们已经证明了我国的“生产率—利润率—投资率—增长率”模式，但是，上述分析似乎存在一些缺陷。注意到改革以来，我国生产中采用的各种要素成本不断上升，特别是煤、石油等资源类价格上涨较快，幅度较大，超过了产成品价格的上涨幅度。这些成本因素的上升不仅对资本回报率可能发生影响，同时对生产率和增长率可能也会发生影响①傅东平(2009)发现，不同要素成本的提高对生产率的影响不同。资源类价格提高会使生产率下降，而资本品价格上涨导致TFP的升高，同时，工资对生产率影响不显著。。

因此，为了检验上文中结论的稳健性，我们在下面的分析中加入资源品价格指数代表的成本因素，进行六变量的脉冲响应分析。考虑数据的可得性，资源品价格指数使用原材料、燃料和动力购进价格指数进行替代。此时的六变量的正交化脉冲响应函数如图3 所示②由于PVAR 模型估计的系数意义不大，此处我们不再报告PVAR 估计的结果。。可以发现，考虑了资源品价格的变动并不会对先前的结论造成实质性的影响，上文中“生产率—利润率—投资率—增长率”的良性循环仍然成立。新加入的变量即资源品价格的一个正向冲击确实会导致资本回报率的显著下降，并且资本品价格的上升会导致投资的减少，这与直觉相一致。与傅东平的研究结论不同的是［40］，我们发现，资源品价格的上升对生产率的影响不显著。这可能是由于我们的资源品价格是作为各种要素成本的一个总体概况，而不同要素成本的上升对生产率影响的方向不同，从而相互抵消的缘故。

另外，考虑到我们此处测度全要素生产率的方法较为前沿，以往的研究较少采用，我们也利用Solow 方法测算的全要素生产率进行了重新检验，发现结论基本一致，只是生产率和投资增长对经济增长的作用更持久①在Solow 测算方法下，这一作用维持到10 期以后仍存在。，并且发现，资本深化对生产率具有显著正向影响②这里不再列出结果，有兴趣的读者可以向作者索要。。因此可以认为，我们的结论是较为稳健的。

图3 考虑了资源品价格指数后的脉冲响应函数图

四、总结

正确解读“中国奇迹”的原因，不仅是改革以来我国社会主义建设经验的回顾和总结，也是今后发展的展望和指导。但是，现有文献对“中国奇迹”的解释，低估了资本形成的作用，甚至认为依靠高投资的“中国奇迹”是不可持续的。有鉴于此，本文借助面板VAR 的方法，利用我国28 个省市1978-2010年的面板数据，从资本回报率的视角对中国奇迹提出了一个新的解释。本文发现，中国奇迹可能是生产率、利润率、投资率和增长率良性互动的结果。具体而言，改革以来，我国生产率提高和国民收入的提高相互促进，并共同提升了资本回报率。在高资本回报率的驱动下，投资增长旺盛，一方面直接带动了经济的快速增长和国民收入的提高;另一方面在一定程度上通过“干中学”效应促进了我国生产率的提升。而生产率的提高和国民收入的提高又一次相互促进，从而形成了一个良性循环。

需要说明的是，我国得以保持上述良性循环的重要原因在于较高的资本回报率，而较高的资本回报率又来源于生产率的快速提升。虽然在我们的研究中，投资可以通过“干中学”效应在一定程度上提升生产率水平，但是这种作用对生产率的提升毕竟有限，从而对资本回报率的提升作用也有限;另一方面，投资的增长会导致资本深化，从而降低资本回报率。因此，要保持我国目前这种“生产率—利润率—投资率—增长率”的良性循环，关键要在不断提高生产率水平上下功夫。改革之初，农村实行的家庭联产承包责任制改革和城市实行的工业改革，从制度层面上大大提升了生产率水平。近年来，加入世贸组织、国企改革和金融体制改革，又一次对我国生产率水平给予了一个正向的外生冲击。从这个意义上说，“改革是中国最大的红利”，今后要保持“中国奇迹”，就要加大改革力度，从而解放生产力;同时，要不断鼓励创新，增加教育投入，提高人力资本水平，从而促进生产率的不断进步，保证生产率、利润率、投资率和增长率的良性循环。

［1］Lin J Y，Cai F，Li Z．The China miracle:Development strategy and economic reform，Hongkong:Chinese University Press，2003．

［2］Charles A，Fontana G，Srivastava A．“India，China and the East Asian Miracle:a human capital development path to high growth rates and declining inequalities”，Cambridge Journal of Regions，Economy and Society．2011，4(1)．

［3］Y Xu．“The Expansion of Peasant Rationality:An Analysis of the Creators of the“China Miracle”—Challenging Existing Theories and Proposing New Analytical Approaches”，Social Sciences in China，2011，32(1)．

［4］Young A．“The tyranny of numbers:confronting the statistical realities of the East Asian growth experience”，The Quarterly Journal of Economics，1995，110(3)．

［5］Young A．“Gold into Base Metals:Productivity Growth in the People’s Republic of China during the Reform Period”，Journal of Political Economy，2003，111(6)．

［6］经济增长前沿课题组:《高投资、宏观成本与经济增长的持续性》，载《经济研究》2005年第10 期。

［7］郭其友、芦丽静:《经济持续增长动力的转变——消费主导型增长的国际经验与借鉴》，载《中山大学学报(社会科学版)》2009年第2 期。

［8］Bai C E，Hsieh C T，Qian Y．“The Return to Capital in China”，Bookings Papers on Economic Activity，2006，37(2)．

［9］CCER:《我国资本回报率估测(1978—2006)——新一轮投资增长和经济景气微观基础》，载《经济学(季刊)》2007年第3 期。

［10］涂正革、肖耿:《中国经济的高增长能否持续:基于企业生产率动态变化的分析》，载《世界经济》2006年第2 期。

［11］Brandt L，Van Biesebroeck J，Zhang Y．“Creative accounting or creative destruction?Firm-level productivity growth in Chinese manufacturing”，Journal of Development Economic，2012，97(2)．

［12］肖林兴:《中国全要素生产率的估计与分解——DEA-Malmquist 方法适用性研究及应用》，载《贵州财经学院学报》2013年第1 期。

［13］Arrow K J．“The economic implications of learning by doing”，The review of economic studies，1962，29(3)．

［14］Romer P．“Endogenous technological change”，National Bureau of Economic Research，1991．

［15］黄伟力:《中国资本利润率的变动趋势及其影响因素》，载《山西财经大学学报》2007年第8 期。

［16］黄先海、杨君、肖明月:《中国资本回报率变动的动因分析——基于资本深化和技术进步的视角》，载《经济理论与经济管理》2011年第11 期。

［17］孙文凯、肖耿、杨秀科:《资本回报率对投资率的影响:中美日对比研究》，载《世界经济》2010年第6 期。

［18］Shane M，Gale H．“China:A study of dynamic growth”，USDA-ERS Outlook Report No，WRS-04-08，2004．

［19］Kuijs L，Wang T．“China＇s pattern of growth:moving to sustainability and reducing inequality”，China ＆World Economy，2006，14(1)．

［20］郑京海、胡鞍钢、Bigsten Arne:《中国的经济增长能否持续—— 一个生产率视角》，载《经济学(季刊)》2008年 第3 期。

［21］Ding S，Knight J．“Can the augmented Solow model explain China＇s remarkable economic growth?A cross-country panel data analysis”，Journal of Comparative Economics，2009，37(3)．

［22］Ding S，Knight J．“Why has China Grown So Fast?The Role of Physical and Human Capital Formation”，Oxford Bulletin of Economics and Statistics，2011，73(2)．

［23］Solow R M．“Technical change and the aggregate production function”，The review of Economics and Statistics，1957，39(3)．

［24］Acemoglu D，Linn J．“Market size in innovation:theory and evidence from the pharmaceutical industry”，The Quarterly Journal of Economics，2004，119(3)．

［25］Lagakos D．Superstores or Mom and Pops?Market Size，Technology Adoption and TFP Differences．Working Paper，UCLA，2008．

［26］陈丰龙、徐康宁:《本土市场规模与中国制造业全要素生产率》，载《中国工业经济》2012年第5 期。

［27］Syverson C．“Market Structure and Productivity:A Concrete Example”， Journal of Political Economy，2004，112(6)．

［28］Melitz M J，Ottaviano G I．“Market size，trade，and productivity”，The Review of Economic Studies，2008，75(1)．

［29］Barro R J，Sala-I-Martin X．Economic growth，2nd．Massachusetts:MIT Press，2003．

［30］Love I，Zicchino L．“Financial development and dynamic investment behavior:Evidence from panel VAR”，The Quarterly Review of Economics and Finance，2006，46(2)．

［31］Mclean R D，Zhang T，Zhao M．“Why does the law matter?Investor protection and its effects on investment，finance，and growth”，The Journal of Finance，2012，67(1)．

［32］Arellano M，Bover O．“Another look at the instrumental variable estimation of error- components models”，Journal of econometrics，1995，68(1)．

［33］Acemoglu D．Introduction to modern economic growth，Princeton University Press，2008．

［34］司春林、王安宇、袁庆丰:《中国IS-LM 模型及其政策含义》，载《管理科学学报》2002年第1 期。

［35］周明海、肖文、姚先国:《中国劳动收入份额的下降:度量与解释的研究进展》，载《世界经济文汇》2010年第6 期。

［36］周明海、肖文、姚先国:《中国经济非均衡增长和国民收入分配失衡》，载《中国工业经济》2010年第6 期。

［37］Greene W．“Fixed and random effects in stochastic frontier models”， Journal of Productivity Analysis，2005，23(1)．

［38］Wang H，Ho C．“Estimating fixed- effect panel stochastic frontier models by model transformation”，Journal of Econometrics，2010，157(2)．

［39］单豪杰:《中国资本存量K 的再估算:1952 ～2006年》，载《数量经济技术经济研究》2008年第10 期。

［40］傅东平:《中国生产率的变化及其影响因素研究》，载《华中科技大学博士论文》2009年版。