基于极大熵理论求解线性互补问题

杨丹丹，韩海山，李 园

(内蒙古民族大学 数学学院，内蒙古 通辽 028043)

基于极大熵理论求解线性互补问题

杨丹丹，韩海山，李 园

(内蒙古民族大学 数学学院，内蒙古 通辽 028043)

给出了线性互补问题的一种解法，在假设A的特征值大于1时，线性互补问题等价转化为绝对值方程问题，利用极大熵函数给出了求解此类绝对值问题的光滑滑迭代算法，并证明了算法是收敛的，数值实验表明此方法的有效性.

线性互补问题；绝对值方程；极大熵；不动点迭代

线性互补问题是运筹学与计算数学的一个交叉研究领域,已经广泛应用于力学、交通、经济、金融、控制等领域中出现的许多数学模型.在20世纪90年代，研究线性互补问题的求解方法已达到了高潮.通过近几十年的发展，人们不仅改进和丰富了线性互补问题的理论和方法的研究，而且还提出了许多有效的算法[1-4]，例如: 多重分裂法、投影法、光滑牛顿法、非光滑牛顿法、松弛法、内点法、非光滑方程法等. 进一步掌握和研究互补问题的各类算法不仅具有理论意义, 而且具有实际意义.

设A∈Rn×n,q∈Rn,线性互补问题是指:求z=(z1,z2,…,zn)∈Rn, 使得:

(1)

简记作LCP(A,q).

1 问题转换

线性互补问题可以等价转化为绝对值方程，即LCP(A,q)⟹AVE,引进变量ω=Az+q将式(1)等价的改写为:

(2)

令ω=|x|-x,z=|x|+x，由于A的特征值大于1，故(A+I)-1存在，从而：

ω=Az+q⟺x=(A+I)-1(I-A)|x|-(A+I)-1q

显然求解LCP(A,q)问题等价于求x∈Rn满足绝对值方程:

x=(A+I)-1(I-A)|x|-(A+I)-1q

(3)

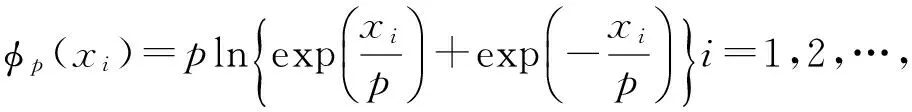
由文献[5]已知φp(xi)具有如下两个性质:

性质1：当p>q时，φp(xi)>φq(xi) ，且当p→0 时，φp(xi)以φ(xi) 为极限；

性质2：∀p>0,0≤φp(xi)-φ(xi)≤pln2.

则公式(3)可以转换为:

x=(A+I)-1(I-A)φp(x)-(A+I)-1q

(4)

其中φp(x)=(φp(x1),φp(x2),…,φp(xn))T.

2 算法及收敛性分析

问题(4)是一个典型的不动点问题，下面给出求解问题(4)的迭代算法.算法步骤如下：

a)任意选取一个初始点x0∈Rn,允许误差ε>0及参数p>0,k:=0;

b)计算xk+1=f(xk)=(A+I)-1(I-A)φp(xk)-(A+I)-1q；

c)若‖xk+1-xk‖≤ε，则停止，得到解x*=xk+1；否则转入步骤b).

迭代公式(4)的Jacobi矩阵为Mk=(A+I)-1(I-A)Λk，其中:

引理1 由算法所产生的序列{x1,x2,x3,…}收敛，且其极限就是问题(4)的解.

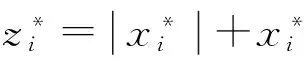
3 数值试验

数值试验运用Matlab 7.0进行编程计算，下面的计算中参数选取如下：ε=1.0e-6，p=0.1或者p=0.01.

例1 求解线性互补问题LCP(A,q)，其中:

调用本文的算法，其中选取n=4,p=0.01，T/s代表迭代时间，单位为秒，选用不同的初值x的结果见表1.

表1 不同初值x0的计算结果

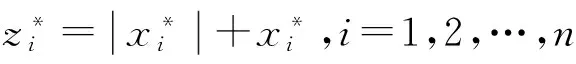
通过上表可以看出本文的迭代法解线性互补问题是十分快速且有效的.

4 结语

本文提出了求解线性互补问题的一种光滑化不动点迭代法，并且证明了该迭代法是收敛的，本算法具有格式简单，存储量小和易于在计算机上实现等优点，为此本文给出的迭代.

[1] Cottle R W,Pang J S,Stone R E.The Linear Complementarity Problems[M].San Diego：Academic Press,CA,1992.

[2] Facchinei F,Pang J S.Finite-dimensional variational inequalities and complementarity problems[M].New York:Vol. I and II. Springer,2003.

[3] 韩继业,修乃华,戚厚铎.非线性互补理论与算法[M].上海:上海科学技术出版社,2006.

[4] 李园,杨丹丹,韩海山.线性互补问题罚函数方法的收敛性分析[J].运筹与管理,2012,21(5):129-134.

[5] LI X S.An efficient method for non-differentiable optimization problem[J].Science in China-Series,1994,24(4):371-377.

[6] 李庆阳，莫孜中，祁力群.非线性方程组的数值解法[M].北京：科学出版社，1999.

SolutionofLinearComplementarityBasedonMaximumEntropyTheory

YANG Dan-dan,HAN Hai-shan,LI Yuan

(College of Mathematics,Inner Mongolia University for Nationalities,Tongliao 028043,China)

In this paper,a method of solution for linear complementary problem is given, under the assumption that the characteristic of the value is greater than 1, the equivalent linear complementary problem into absolute value equation, using the maximum entropy function gives smooth iterative algorithm for solving this kind of absolute value problems ,and proves that the algorithm is convergent and numerical experiments show that the method is effective.

linear complementarity problem; absolute value equation；maximum entropy； fixed point Iterative method

2013-07-29.

内蒙古自然科学基金项目(2011MS0114).

杨丹丹(1984- ),女,硕士生,讲师,主要从事变分不等式与互补问题的研究.

O221.2

A

1008-8423(2013)03-0260-02