一个新的求解线性互补问题的罚函数方法
2013-12-07韩海山杨丹丹
李 园,韩海山,杨丹丹
(内蒙古民族大学 数学学院,内蒙古 通辽 028043)
一个新的求解线性互补问题的罚函数方法
李 园,韩海山,杨丹丹
(内蒙古民族大学 数学学院,内蒙古 通辽 028043)
线性互补问题LCP(A;b)中矩阵A的结构无论对线性互补问题解的存在性、唯一性,还是对算法的收敛性,都有着非常密切的关系.进一步将P-矩阵线性互补问题的非线性罚方程进行推广,证明了线性互补问题的矩阵A在一定假设的基础上,下对角元素均大于等于零时非线性罚方程的解指数次收敛到线性互补问题的解.
运筹学;线性互补问题;P-矩阵;非线性罚方程;收敛
线性互补问题是运筹学的一个重要分支,广泛应用在自然科学、交通控制、管理科学、经济均衡和工程计算等诸多领域,正因为如此,线性互补问题成为数学规划和计算数学中的一个十分热门的研究领域.许多学者对求解线性互补问题的算法进行了深入的研究,提出了许多算法,可归纳为:投影算法、内点法、光滑牛顿法、不动点算法、近似点算法、非光滑牛顿法、矩阵分裂法等[1-4].进一步研究和提出线性互补问题的新型算法不仅具有理论意义,而且也具有重要的实际价值.
本文考虑如下线性互补问题(简记作LCP(A;b)):求向量x=(x1,x2,…,xn)T∈Rn,使得:
Ax-b≤0;x≤0;(Ax-b)Tx=0,
(1)
其中A∈Rn×n;b∈Rn.
令K={y∈Rn|y≤0},则线性互补问题(1)等价于如下的变分不等式问题:求向量x∈K,使得对任意的y∈K,满足:
(y-x)TAx≥(y-x)Tb.
(2)
文献[6]构造了如下关于线性互补问题(1)的非线性罚方程:求xλ∈Rn,使得:
(3)
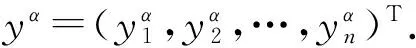
关于线性互补问题(1)的相对应的非线性罚方程(3)的研究,已经取得了如下成果:1984年,Glowinski[4]研究了Rn中变分不等式(2)的形如(3)式的非线性罚方程,证明了在矩阵A对称正定的情况下罚方程的收敛性.2006年,Wang等人[5]将美国期权问题转化成一线性互补问题,利用非线性罚方程(3)对其进行了求解,证明了线性互补问题的矩阵为正定时罚方程的解收敛到互补问题的解.2008年,Yang等人[6]在线性互补问题(1)的矩阵为正定,主对角元素大于零,其余元素均小于等于零的条件下证明了当惩罚因子趋向于无穷大时非线性罚方程(3)的解指数次收敛到线性互补问题的解.同年,Wang等人[7]提出了一个带有扰动项的求解非线性抛物型互补问题的非线性罚方程,但是罚方程的解收敛到互补问题的解仍需正定性假设.鉴于上述罚函数方法的收敛性均依赖于线性互补问题的矩阵的正定性假设.李园等人[8-9]将上述罚函数方法进行了推广,在线性互补问题的矩阵为严格行对角占优的上三角形P-矩阵的条件下证明了非线性罚方程(3)的解指数次收敛到线性互补问题(1)的解.本文进一步将李园等人[9]的P-矩阵线性互补问题的非线性罚方程进行推广,证明了线性互补问题(1)的矩阵A在文献[9]的假设基础上,下对角元素均大于等于零时非线性罚方程(3)的解收敛到线性互补问题(1)的解,并且收敛速率是指数次.
1 预备知识
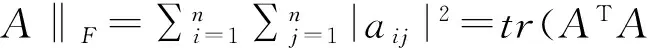
定义1[1]矩阵A=(aij)∈Rn×n是P-矩阵的充要条件是A的所有主子式均大于零.
关于P-矩阵的性质,有如下结论:
引理1[3]A∈Rn×n是P-矩阵的充要条件是:存在一常数c>0,使得对于任意的向量x∈Rn,存在一下标k=k(x),1≤k≤n,满足:
xk(Ax)k≥c‖x‖2.
其中xk表示x的第k个分量,(Ax)k表示Ax的第k个分量.
关于矩阵的F-范数‖·‖F与向量的欧式范数‖·‖的相容性,有如下结论:
引理2[10]设A∈∈Rn×n,x∈∈Rn,则:‖Ax‖≤‖A‖F·‖x‖.
2 非线性罚方程(3)解的性质
本节将讨论非线性罚方程(3)的解的性质,给出非线性罚方程(3)的解收敛于线性互补问题(1)的解的充分条件.首先对线性互补问题(1)中的矩阵A作如下假设:
(A1)A是P-矩阵;

(A3)矩阵A的奇异值均大于1.
在假设(A1)的条件下,线性互补问题(1)有唯一解.根据上面的假设,首先建立下面的定理.
定理1 设x=(u1,u2,…,un)T∈Rn是非线性罚方程(3)的解,若x满足下面条件之一:
(i)xλ的分量均小于等于零;
(ii)xλ仅有一个正分量,其余分量均小于等于零;
(iii)xλ有m(2≤m (4) (5) 证明(i):若xλ的分量均小于等于零,此时[xλ]+=(0,0,…,0)T于是‖[xλ]+‖p=0;‖[xλ]+‖=0,所以式(4)和(5)显然成立;下面仅证明情况(iii),对于情况(ii)可类似证明. (6) A11=I1+L1+U1=L1+(I1+U1)=L1+K1, 其中I1,L1和U1分别是A11的对角、下三角和上三角矩阵,K1=L1+U1,则: (7) 对式(7)应用Hölder不等式,得到: ‖[xλ]+‖2, 于是: c1‖[xλ]+‖2≤[xλ 即: 不等式两端同时开方后,得: 证毕. 由定理1,可以得到下面的收敛性定理. 定理2 设x∈Rn和x∈Rn分别是线性互补问题(1)和非线性罚方程(3)的解,其中x满足定理1的条件.如果rλ=x+[xλ]-=(r1,r2,…,rn)T≤0且对其任意两个不为零的分量ri和rj均有|ri|≥|rj|,则存在一个与n,x,xλ和λ均无关的正数C,使得: (8) 其中[xλ]-=-min{xλ,0},λ和k是式(3)中定义的参数. 证明由前面[xλ]+和[xλ]-的定义,有xλ=[xλ]+-[xλ]+,于是: 随着网络的发达,电子商务渐渐火热起来,这一节日就被商家所利用,以光棍为嚎头制造单身人士要在这一天购物的气氛。2009年淘宝商城的管理层首次将11月11日选用为淘宝购物狂欢节,造就了高达0.5亿元的销售额,从此,“双十一”被越来越多的消费者铭记,“双十一”所产生的销售额逐年攀升。这种从节日到节日的文化转型为“双十一”的成功塑造解决了尤为关键的一步,让众多消费者尤其是作为新世纪知识分子的大学生一代以最快的速度接受并记住。 x-xλ=x+[xλ]--[xλ]+=rλ-[xλ]+, (9) 其中rλ=x+[xλ]-.令υ=x-rλ,由rλ的定义知υ=x-rλ=-[xλ]-≤0,于是υ∈K,在式(2)中令y=υ后,得: (10) (11) 将式(11)和式(12)相加后,有: (12) 而: (13) 将式(9)代入式(13)中,得: (14) 设A=I+L+U=L+(I+U)=L+K,其中I;L和U分别是矩阵A的对角、下三角和上三角矩阵,K=I+U.于是: (15) 根据引理2,不等式(15)的右端: ‖rλ‖·‖A[xλ]+‖≤‖rλ‖·‖A‖F·‖[xλ]+‖ (16) 又由引理1,有: ‖rλ‖2, (17) 其中c2是常数. 由式(15)~(17),得到: c2‖rλ‖2≤‖rλ‖·‖A‖F·‖[xλ]+‖, 所以: (18) 综合式(5),(9),(18)和三角不等式,得: 证毕. 本文进一步将李园等人[9]的P-矩阵线性互补问题的非线性罚方程进行推广,证明了线性互补问题(1)的矩阵A在文献[9]的假设基础上,下对角元素均大于等于零时非线性罚方程(3)的解收敛到线性互补问题(1)的解,并且任然具有指数次的收敛速率,进一步改进了罚函数方法. [1] Cottle R W, Pang J S, Stone R E. The Linear Complementarity Problems[M].Aca-demic Press,San Diego,CA,1992. [2] Facchinei F, Pang J S. Finite-dimensional variational inequalities and complementar-ity problems[M].New York: Springer,2003. [3] 韩继业,修乃华,戚厚铎.非线性互补理论与算法[M].上海:上海科学技术出版社,2006. [4] Glowinski R. Numerical methods for nonlinear variational problems[M].New York:Springer-Verlag,1984. [5] Wang S,Yang X Q,Teo K L.Power penalty method for a linear complementarity problems arising from American option valuation[J].Journal of Optimization Theory and Applications,2006,129(2):227-254. [6] Wang S,Yang X Q.Power penalty method for linear complementarity problems[J].Operations Research Letters,2008,36(2):211-214. [7] Wang S,Huang C S.A power penalty method for solving a nonlinear parabolic complementarity problem[J].Nonlinear Analysis,2008,69(4):1125-1137. [8] Li Y,Han H S,Li Y M,et al.Convergence analysis of power penalty method for three dimensional linear complementarity problems[J].Intelligent Information Management Systems and Technologies,2009,5(3):191-198. [9] 李园,杨丹丹,韩海山.线性互补问题罚函数方法的收敛性分析[J].运筹与管理,2012,21(5):129-134. [10] 张贤达.矩阵分析与应用[M].北京:清华大学出版社,2004. 声明 本刊已许可中国学术期刊(光盘版)电子杂志社在中国知网及其系列数据库产品中,以数字化方式复制、汇编、发行、信息网络传播本刊全文。该著作使用费及相关稿酬,本刊均用作为作者文章发表、出版、推广交流(含信息网络)以及赠送样刊之用途,即不再另行向作者支付。凡作者向本刊提交文章发表之行为即视为同意我刊上述声明。 湖北民族学院学报编辑部 ANewPenalizedMethodforSolvingLinearComplementarityProblems LI Yuan,HAN Hai-shan,YANG Dan-dan (College of Mathematics,Inner Mongolia University for Nationalities,Tongliao 028043,China) The structure of matrix A in the linear complementarity problem LCP(A;b) plays an important role in both the existence, uniqueness of the solution and the convergence of algorithms. In this paper,we further generalize the nonlinear penalized equation for solvingP-matrix LCP(A;b) and prove that the nonlinear penalized equation converges to that of the LCP(A;b) at an exponential rate under the condition that the lower diagonal elements of matrixAare greater than or equal to zero based on Li′s hypothesis. operations research;linear complementarity problem;P-matrix;nonlinear penalized equation;convergence 2013-07-29. 内蒙古自然科学基金项目(2011MS0114). 李园(1985- ),男,讲师,主要从事变分不等式与互补问题的研究. O221.2 A 1008-8423(2013)03-0262-05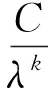
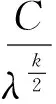

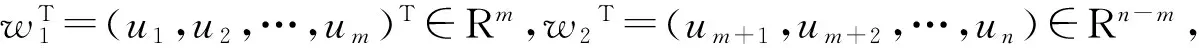
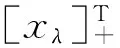


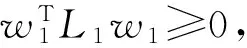
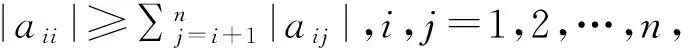

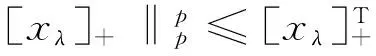
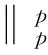
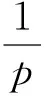
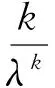
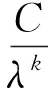

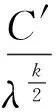


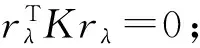
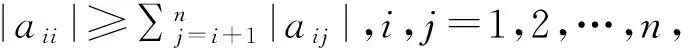


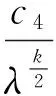
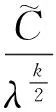
3 结语
