某些对称群关于元素阶的和的刻画

吴 超，刘 静，沈如林

(湖北民族学院 数学系，湖北 恩施 445000)

某些对称群关于元素阶的和的刻画

吴 超，刘 静，沈如林

(湖北民族学院 数学系，湖北 恩施 445000)

设G是有限群，记ψ(G)为群G所有元素阶的和.证明了如果G的阶等于对称群Sn的阶，则有ψ(Sn)≤ψ(G),等号成立当且仅当G≅Sn,这里n=1,2,3,4,5,6.

有限群；元素阶；对称群；Sylow子群

1 引言与引理

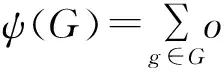
定理1 设G是120阶非对称有限群，那么ψ(S5)<ψ(G)，这里S5为5次对称群.

定理2 设G是720阶非对称有限群，那么ψ(S6)<ψ(G)，这里S6为6次对称群.

首先给出一些引理.

引理1 设M有限群G的正规Hall子群.设x∈G且o(x)=pα(p是素数),那么:

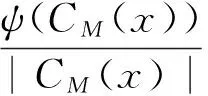
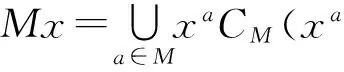
引理2 设G是120阶有限群.如果G含有15阶元，那么ψ(G)>471.

证明首先，假设G中至少含有3个15阶循环子群，那么G中至少含有3φ(15)=24个15阶元，从而G中至多含有95个非15阶元.因此ψ(G)≥24(15)+95(2)+1=551>471.

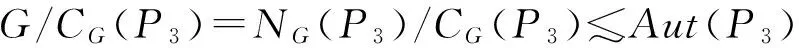
ψ(CG(P3))=ψ(CG(P3)/P3)ψ(P3)≥ψ(5×|4)ψ(P3)>471.

引理3 设G是36阶群，那么ψ(G)≥111.

证明因为|G|=36，所以n3(G)=1或4.

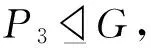
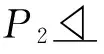
引理4 设G是720阶群.若n5(G)=1或16，那么ψ(G)>3271.

若n5=16，那么|NG(P5)|=45，这里P5∈Syl5(G).因为45阶群是交换群，所以NG(P5)=CG(P5).于是G有正规5-补M且|M|=24·32.由引理1:

这里1≠x∈P5.

2 定理1的证明

不难计算ψ(S5)=471.首先假设G可解.那么G必含有15阶子群，从而G含有15阶元.由引理D，ψ(G)>471，即ψ(G)>ψ(S5).

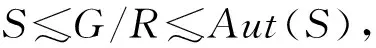
3 定理2的证明

不难计算ψ(S6)=3271.首先假设G可解.从而由文献[4] ，n5(G)=1或16.因此由引理4，ψ(G)>3271，即ψ(G)>ψ(S6).

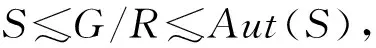
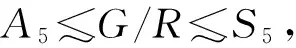
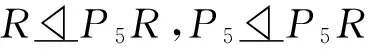
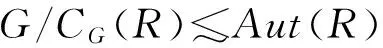
ψ(G)≥6ψ(P5×R)-5ψ(R)=(6ψ(P5)-5)ψ(R)≥(6ψ(P5)-5)ψ(A4)>3271，即ψ(G)>ψ(S6).

4 结语

注意，当n=1,2,3,4时，由文献[7]直接计算知结论成立.上面考虑的群都是很特殊的对称群，如果考虑一般的对称群，问是否还有类似于上面的结果，即有如下猜想：

猜想： 设G是n!阶非对称有限群，那么ψ(Sn)<ψ(G)，这里Sn为n次对称群.

[1] Amir I,Jafarian Amiri S M,Isaacs I M.Sums of element orders in finite groups[J].Commun Algebra,2009,37(9):2978-2980.

[2] Amiri H,Jafarian Amiri S M.Sum of element orders on finite groups of the same order[J].J Algebra Appl,2011,10(2):187-190.

[3] Jafarian Amiri S M.Characterzation ofA5andPSL(2,7) by sum of element orders[J]. International Journal of Group theory,2013,2(2):35-39.

[4] Hall P.A note on soluble groups[J].J London Math Soc,1928,3(2):98-105.

[5] Hall M. On the number of Sylow subgroups of a finite group[J].J Algebra,1967，7:363-371.

[6] Song-liang Chen.36阶群的完全分类[J].烟台师范学院学报,2002,18(4):241-246.

[7] Thomas A D,Wood G V.Group tables[M].United Kingdom:Shiva Publishing Limited,1980.

ACharacterizationofSomeSymmetricGroupsbytheSumofElementOrders

WU Chao,LIU Jing,SHEN Ru-lin

(Department of Mathematics, Hubei University for Nationalities,Enshi 445000,China)

LetGbe a finite group. Writeψ(G) to denote the sum of orders of the elements of G.In this paper, we prove that if the order ofGis equal to the order ofSn, thenψ(Sn)≤ψ(G) andψ(G)=ψ(Sn) if and only ifG≅Sn,wheren=1,2,3,4,5,6.

finite group；order of elements；symmetric group；Sylow subgroup

2013-06-13.

国家自然科学青年基金项目(11201133).

吴超(1988- )，男(土家族)，硕士生，主要从事有限群的研究.

152.1

A

1008-8423(2013)03-0257-03