一类振荡无穷积分的一种数值算法

蒋冰峰，熊小勇，胡艳霞

(湖北民族学院 理学院， 湖北 恩施 445000)

一类振荡无穷积分的一种数值算法

蒋冰峰，熊小勇，胡艳霞

(湖北民族学院 理学院， 湖北 恩施 445000)

振荡函数无穷范围积分的数值计算方法是先求出振荡函数的各级零点，根据被积函数在相邻零点间积分，再把积分结果求和.但是，求和的结果收敛性质非常差.我们采用W外推算法，来加快求和结果的收敛性.我们以一个简单的例子说明W外推算法的有效性.

振荡函数；无穷积分；算法

在科学计算及工程技术应用中，经常会涉及到计算振荡函数的无穷积分，形如[1-3]:

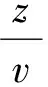
(1)

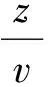
形如式(1)的二维数值积分非常复杂，为了简便性，也不失一般性，先讨论以下一维振荡函数f(x)的无穷积分(a≥0)：

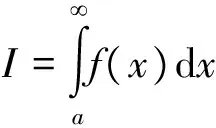
(2)

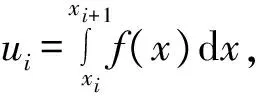
在处理积分或数列的外推方法中，常用的有Euler 变换，ε算法和W变换[4].其中由Sidi建立的W变换[5-7]是非常有效的外推算法[8].在本文中，根据W变换编写外推算法程序，并以一个简单的积分为例，介绍如何应用外推算法计算振荡积分的无穷积分.

1 W变换

根据振荡函数f(x)的一系列零点x1,x2,x3,…，构造如下函数:

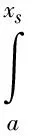
(3)

(4)

(5)

(6)

(7)

其中s,p=0,1,2，….

2 ISE方法求积分流程

以下将用实例来说明如何使用ISE方法求解振荡函数的无穷积分.

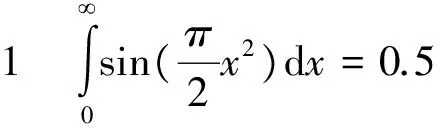
(8)

第一步：由例子可知x0=0，然后根据被积函数求其零点x1,x2,x3,…本例子中，振荡函数为三角函数，其零点非常容易求得.式(1)中的振荡函数J0的零点的求解要复杂得多，但是根据Temme的算法[9-10]，CERNLIB已有现成的算法Dbzejy() 计算各种类型贝塞尔函数的零点[11].

第二步：求被积函数sin(πx2/2)在所有零点间隔[xi,xi+1]的ψ(xi)以及G(xi).出于计算的精确性，此处积分程序可采用Piessens等人[12]自适应算法基础上的子程序Dqag()或Dqng()[13-14].

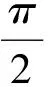
从表1中可以看出，即使是积分上限取到被积函数的第1000个零点，计算结果0.507114061665686同标准结果相比，差距仍然是非常明显，不可忽略的.第二，计算结果在标准值0.5附近振荡，这也反应了被积函数的振荡性质.

第三步：根据ψ(xi)以及G(xi)和W变换算法，编写外推算法子程序.根据ψ(xi)以及G(xi)和外推程序，得到最终结果.

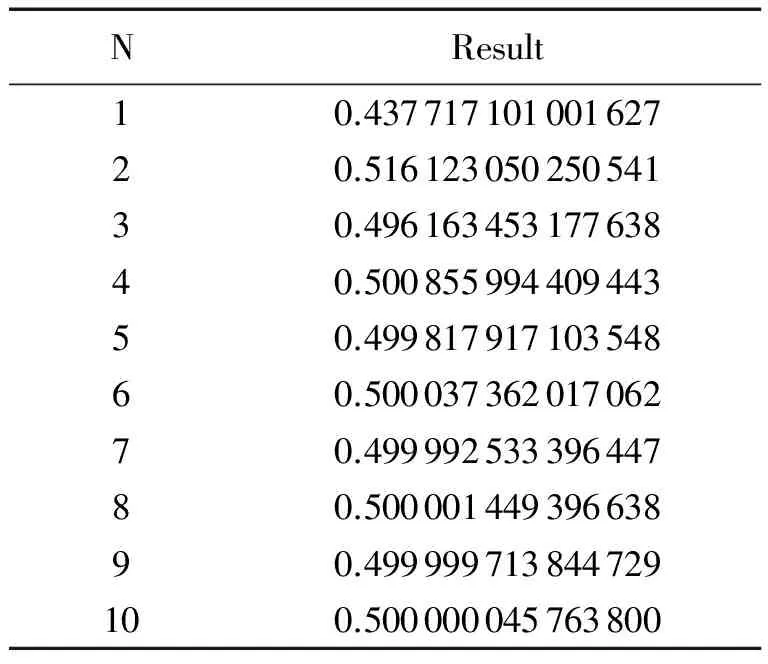
只需要式(8)中前10个零点间隔的积分结果，采用W-transformation外推算法(4)(5)(6)(7)，就可以得到精度非常高的结果，见表2.

表1无外推算法时991-1000个零点积分和结果

Tab.1 Results for partial sums for 991 to 1000 zeros of the integrand without extrapolation

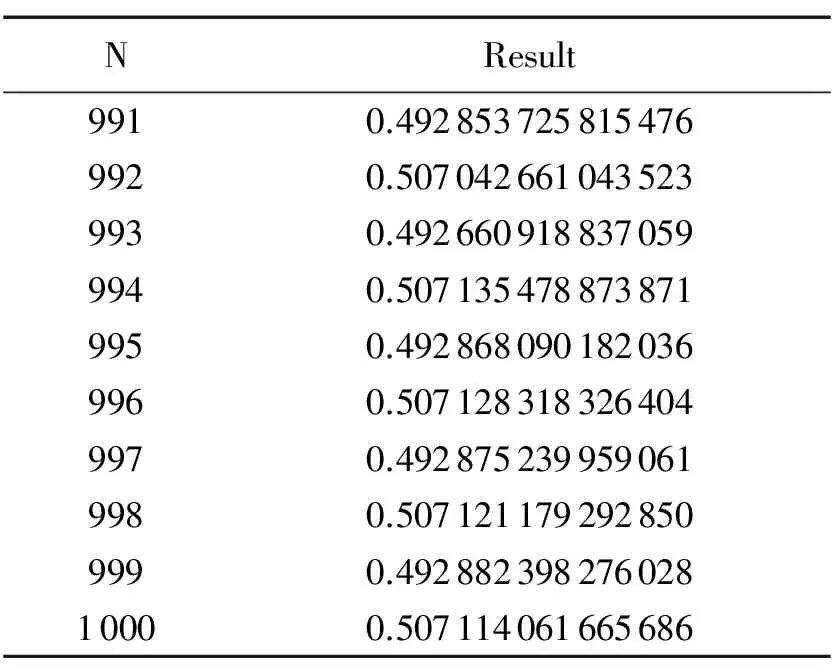
NResult9910．4928537258154769920．5070426610435239930．4926609188370599940．5071354788738719950．4928680901820369960．5071283183264049970．4928752399590619980．5071211792928509990．49288239827602810000．507114061665686

表2 W-transformation所得结果

Tab.2 Results for the first ten zeros of the integrand with W-extrapolation

NResult10．43771710100162720．51612305025054130．49616345317763840．50085599440944350．49981791710354860．50003736201706270．49999253339644780．50000144939663890．499999713844729100．500000045763800

PROGRAM MAIN

double precision a,abserr,b,f,epsabs,epsrel,result,c1,c2,pi,

& psi,hi,i,x,m,n,w,resul

integer ier,neval,lst,limst,lsta,limsta,p,s,n1,l,j,pl,jl,i1,i2,i3

parameter(limst=50)

dimension hi(-1:limst),psi(-1:limst), x(-1:limst),

& m(-1:limst,0:limst)

& ,n(-1:limst,0:limst), w(-1:limst,0:limst)

external f

data pi /3.1415926535 8979323846 2643383279 50 d0/

epsabs=0.0d0

epsrel=1.0d-6

L=Limst-1

x(-1)=0.0d0

**********************************************

****** 算法程序求被积函数的前50个零点

**********************************************

do 10 i1=0, limst

x(i1)=sqrt(2.0d0*(i1+1))

10 continue

IF(lst.le.(-1)) hi(lst)=0.0D0

IF(lst.lt.(-1)) psi(lst)=0.0D0

**********************************************

****** 在相邻零点间被积函数的积分及结果的和

**********************************************

do 20 lst=-1,l

c1=x(lst)

c2=x(lst+1)

call dqng(f,c1,c2,epsabs,epsrel,result,abserr,neval,ier)

Psi(lst)=result

hi(lst+1)=hi(lst)+psi(lst)

write(*,*)lst, psi(lst), hi(lst+1)

20continue

**********************************************

****** 应用外推算法，得到最终结果resul

**********************************************

call mWextra(l,psi,hi,x,m,n,w,resul,epsrel)

write(*,*)resul

stop

end

**********************************************

****** 根据W算法编写的外推算法子程序

**********************************************

subroutine mWextra(L,psi,hi,x,m,n,w,resul,epsrel)

integer l,p,s,j,jl

double precision psi,hi,x,m,n,w,resul,epsrel

dimension psi(-1:l+1),hi(-1:l+1),x(-1:l+1),m(-1:l+1,0:l+1),

& n(-1:l+1,0:l+1),w(-1:l+1,0:l+1)

do 30 s=0,L

m(-1,s)=hi(s)/psi(s)

n(-1,s)=1.0d0/psi(s)

m(0,s)=(m(-1,s)-m(-1,s+1))/(x(s)**(-1)-x(s+1)**(-1))

n(0,s)=(n(-1,s)-n(-1,s+1))/(x(s)**(-1)-x(s+1)**(-1))

write(*,*)s,m(-1,s),n(-1,s)

write(*,*)s,m(0,s),n(0,s)

30 continue

do 40 p=1,l

jl=l-p

do 50 j=0,jl

m(p,j)=(m(p-1,j)-m(p-1,j+1))/(x(j)**(-1)-x(j+p+1)**(-1))

n(p,j)=(n(p-1,j)-n(p-1,j+1))/(x(j)**(-1)-x(j+p+1)**(-1))

50 continue

w(p,0)=m(p,0)/n(p,0)

write(*,*) p, w(p,0)

if(abs(w(p,0)-w(p-1,0)).le.epsrel) then

resul=w(p,0)

write(*,*)"The final result"

write(*,*) p, resul

go to 60

end if

40 continue

if(abs(w(l,0)-w(l-1,0)).gt.epsrel) then

write(*,*)"please enhance the L"

end if

60 return

end

**********************************************

****** 定义被积函数

**********************************************

double precision function f(x)

double precision x

data pi /3.1415926535 8979323846 2643383279 50 d0/

f=sin(pi/2*x**2)

return

end

[1] Jiang B F,Li J R.The polarized charge distribution induced by a fast parton in the viscous quark-gluon plasma[J].J Phys G:Nucl Part Phys,2012,39:1-10.

[2] Jiang B F,Li J R.The wake potential in the viscous quark-gluon plasma[J]. Nucl Phys A, 2011, 856:121-133.

[3] Jiang B F,Li J R Non-abelian effects on wake potential in quark-gluon plasma[J]. Nucl Phys A, 2010,832:100-111.

[4] Davis P J,Rabinowitz P. Methods of Numerical Interaction[M]. London: Acadamic Press,1984.

[5] Sidi A. The numerical evaluation of very oscillatory infinite integrals by extrapolation[J].Math Comput,1982,38:517-529.

[6] Sidi A. A user-friendly extrapolation method for oscillatory infinite integrals[J]. Math Comput,1988,51:249-266.

[7] Sidi A. Practical extrapolation methods[M]. Cambridge: Cambridge Univ Press,2003.

[8] Lucas S K, Stone H A.Evaluating infinite integrals involving Bessel functions of arbitrary order[J].J Comput Appl Math, 1995, 64:217-231.

[9] Temme N M. On the numerical evaluation of the ordinary Bessel function of the second kind[J].J Comput Phys, 1976, 21:343-350.

[10] Temme N M.An algorithm with Algol 60 program for the computation of the zeros of ordinary Bessel functions and those of their derivatives[J].J Comput Phys,1979,32:270-279.

[11] Piessens R， Doncker-Kapenga E De， Uberhuber C W,et al. A subroutine package for automaticintergration[M].Berlin：Spinger，1983.

TheNumericalAlgorithmofInfiniteIntegralsInvolvingaKindofOscillatoryFunction

JIANG Bing-feng,XIONG Xiao-yong,HU Yan-xia

(School of Science,Hubei University for Nationalities,Enshi 445000,China)

The method of evaluating infinite integrals involving oscillatory function is divided into three steps: finding zeros of the oscillatory function, doing integral at its zeros and forming a sequence of partial sums, using extrapolation to accelerate convergence to obtain the final result. In this paper, W-transformation is used to accelerate the convergence of the infinite integral of oscillatory function.

Oscillatory function; infinite integral;aglorithm

2012-11-13.

国家自然科学基金项目(11147012)；湖北民族学院博士启动基金项目(MY2011B002).

蒋冰峰(1977- ),男，博士，讲师，主要从事夸克物质理论研究.

O241.4

A

1008-8423(2013)02-0163-04