求解非连通图旅行商问题的改进遗传算法*
2013-12-07孔令夷
孔令夷
(西安邮电大学 管理工程学院,陕西 西安 710061)
遗传算法 GA(Genetic Algorithm)遵循“适者生存”的规律,通过模仿自然选择而不断搜索最优解。GA的求解过程包括选择(Selection)、交叉(Crossover)、变异(Mutation)操作。由于GA对问题的限制不多,对目标函数的数学特性要求也不严格,因而相比传统的运筹规划方法,在处理复杂问题时显得游刃有余,几乎都能找到最优解。GA的应用非常广泛,适用于处理大多数科学与工程复杂问题,应用价值很高。其中旅行商问题具有高度的计算复杂性,在图论中最具代表性,已被证明是高维非线性完全问题NPC(Non-deterministic Polynomial Complete Problem)[1-2],多年来都是理论界与企业界面临的难题,如何将智能优化算法应用于这一难题的全局优化求解,也成为了众多学者研究的对象[3-4]。
1 问题描述
现实中的旅行商问题一般都会有各种约束或限制,而非连通图就是一个典型的例子,即旅行商要经过的某些目的地(城市)之间存在障碍物,如山川、农田等,不能直接连通,只有通过其他地点间接到达。旅行商经过的所有地点将构成非连通图,如图1所示。

本文的研究目的是寻找最短路径,将旅行商的成本降到最低。该路径经过的所有N个城市,除了起点以外,都要经过且只经过1次,最终回到起点,符合旅行商遍历所有城市实现销售额最大化的实际情形。设有N个城市的集合 C={c1,c2,…,cN},每两个城市之间的距离为 d(ci,cj)∈R+,其中,ci,cj∈C(1≤i,j≤N)
求使目标函数

最 小 的 路 径 序 列{cΠ(1),cΠ(2),…,cΠ(N)}, 其 中 П(1), П(2),…,П(N)是 1,2,…,N的全排列。
2 改进遗传算法设计
求解旅行商问题的传统方法存在明显的缺陷:设计变量少,与现实不相符;假设较多,对目标函数有可微或连续的诸多限制,在求解中会产生非可行解,难以得到全局最优解。传统求解方法不能很好地模拟实际问题的各种复杂情境,尤其在非连通图约束的情况下,运筹规划等传统求解方法更是难以应对,无法客观准确地把实际问题转化为数学模型。相比传统的方法,GA的优势在这种情况下能够较好地显示出来:(1)它并不是直接处理路径中的显性变量,而是对变量编码任意组合成串,即染色体,这才是GA处理的对象,可见其对旅行商问题几乎没有什么限制。(2)在求最优解的过程中,能够接受各种类型的目标函数,体现了GA的普适性。(3)传统求解方法往往是从一个初始解开始,经过多次迭代的过程求得最优解,求解线路单一。而GA不是沿着一条线,而是基于面上的一代种群求解,容易保留更多优良的个体,淘汰较劣个体,几代遗传之后可保证得到全局最优解;GA的择优去劣过程,只以个体的适应度值作为判断,不需要补充更多信息,操作简便;GA基于概率论的知识进行遗传操作,求出具有较高可信度的最优解,且不排除进一步的改善,确保了其灵活性。因此,GA适合于求解高维、大样本、非线性、非结构性的复杂问题[5]。
传统遗传算法 TGA(Traditional Genetic Algorithm)严重依赖于参数设置和交叉变异算子,存在早熟收敛的缺陷。近年来,国内外学者针对不同约束条件下的旅行商问题,纷纷提出了改进遗传算法IGA(Improved Genetic Algorithm)。BIERWIRTH C等在对各类交叉操作实验对比的基础上,提出了优先保留交叉法PPX(Precedence Preservation Crossover),克服了TGA的上述缺陷[6]。MURATA T等通过仿真实验,提出平移变异SCM(Shift Change Mutation),引入局部邻域搜索,确保子代遗传质量并加快算法收敛[7]。
2.1 编码方式
本研究的编码采用基于旅行商需要遍历所有城市的次序,这也是最常用的编码方式,以有限的城市数量作为搜索范围,有助于提高搜索效率。设S=(1,5,4,3,2,6,7),可以看成是从城市1出发,依次经过城市5、4、3、2、6、7,最终回到起点的一个路径。
2.2 初始种群生成
初始种群的质量对后续的优化求解具有关键作用。若按随机方式产生初始种群,将难以保证其满足非连通约束,容易产生很多非可行解,从而降低了TGA的效率。拟将其改为综合随机法与贪心法来生成初始染色体种群。贪心法是指每一步都求局部最优。
2.3 交叉变异操作
基于旅行商遍历城市次序的编码方式,个体内部基因存在先后关系,若在交叉变异操作中破坏了这种自然关系,则有可能产生大量不可行子代个体,造成早熟收敛或冗余迭代[8-9]。因此拟选用PPX和SCM操作。PPX是随机产生的两个父代个体,并产生一个等长的{1,2}随机串。扫描随机串,如果第k位是1,则提取第一个父代染色体最左边的城市号作为子代第k位;如果第k位是2,则提取第二个父代染色体最左边的城市号,然后删除两个父代中的该城市号,重复以上操作,直到随机串被扫描完。PPX与映射、次序或循环交叉相比,可更好地继承优良基因。
SCM操作是指随机选择插入码和插入点,进行平移操作。比如S=(1,5,4,3,2,6,7),若随机选取插入码为6,插入点为 5与 4之间, 则 S′=(1,5,6,4,3,2,7),SCM与对换变异、目标导向变异等相比,更好地保持了基因之间的先后次序,继承了父代的优良性。
2.4 局部邻域搜索
IGA拟引入局部邻域搜索,这是旅行商问题中常用的一种子代择优方法,有助于进一步加快算法的收敛,缩短求最优解的运行时间。其操作内容是:以交叉变异操作产生的子代个体为基体,对每个基因采用右邻基因交换的方法产生新的局部邻域子代个体。例如S′=(1,5,6,4,3,2,7),将基因 2与其右邻的基因 7交换,就能生成一个新个体 S′=(1,5,6,4,3,7,2)。 因此,局部邻域搜索能产生N-1个局部邻域子代个体,从中选择具有最大适应度的邻域个体与基体再做比较,以适应度大者为更新后的子代基体。
2.5 选择操作及适应度函数的建立
选择操作是对生物进化论“适者生存”思想的体现,越优良的个体具有越大的概率进入下一代,种群性能就会随着进化而不断优化。采用轮盘赌法(Roulette Wheel Selection),保证将种群中最优个体随机替换掉下一代的某个体,对于IGA能够不断寻优具有关键作用。
适应度函数是评价个体优劣的指标。由于本文研究的路径问题是最小化路径长度,因此,本研究适应度函数取线性定标,即有:

式中,α为预先设定的常数;N为城市的数目;M为包含所有城市的最小正方形的边长;Td就是根据式(1)计算得出的实际行进路径长度,即目标和数值。
为了避免产生大量非可行解,本研究IGA作如下特殊处理:
为解决这一问题,可通过对非连通城市间距离进行特殊处理,来保证GA的优良特性不会受到影响,而且可以更容易地找到该问题的可行解。如上文所述,城市cp,cq之间存在障碍物,假设个体S包含基因片段(…,cp,cq,…)或者(…,cq,cp, …), 则有:
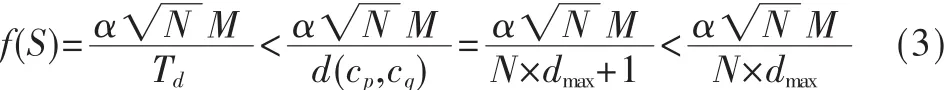
因此,在特殊处理后,若个体S中存在非连通城市相邻,则必会出现其适应度值小于,随着进化历程而逐渐被淘汰,因此就排除了非连通城市相邻的情况。反之,式(4)若成立,则个体S必定为可行解,用反证法可证出,此处从略。

如果用GA求解非连通图旅行商问题,求出最优解的适应度值小于,则可以断定该最优解不成立。
2.6 算法步骤
(1)初始化。设置预定常数、最大迭代次数、交叉概率 Pc、变异概率 Pm等参数。
(2)采用遍历城市排序的编码方法,结合随机选取与贪心法来生成初始种群。
While(迭代次数≤最大迭代次数)do
(3)按Pc概率执行交叉操作,按 Pm概率执行变异操作,再做局部邻域搜索。
(4)根据 f(S),用轮盘赌法执行选择操作,确定子代个体,保证优良个体保留下来。
(5)求得最大适应度值的个体作为最优解。
(6)检验最优解的适应度值是否满足式(4),若满足,则可行;否则为非可行解。
End While
3 算法检验与分析
使用Matlab R2009a分别对文中IGA和TGA进行编程,在2.53 GHz CPU,2.0 GB内存的PC上运行,选取我国31个中心城市的地理数据用于算法检验[10]。设交叉概率 Pc=0.2,变异概率Pm=0.5,最大迭代次数MaxItr=1 000,算法检验结果如表1所示。在求最优解方面,IGA的最满意值为15 383 km,如图2所示。略优于TGA的最满意值15 387 km,如图3所示。说明IGA取得了本例的最优解,达到了算法改进的目的。究其原因,主要是由于TGA在初始种群生成方面产生了大量不可行解和在交叉变异过程中缺失局部邻域择优能力。即正是由于IGA引入局部邻域搜索操作,从而确保了子代个体快速持续地向最优解收敛。

表1 两种算法的检验结果
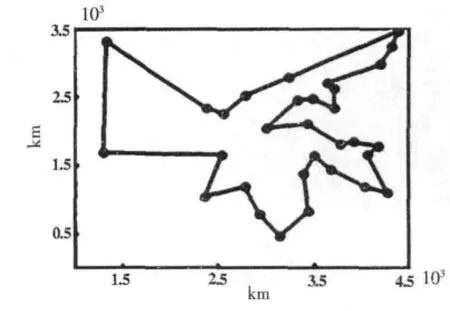
图2 IGA的最满意值

图3 TGA的最满意值
同时,对比两种算法的极差也能看出,IGA的种群离散程度较小,向最优解的集聚性较高,向最优解的收敛性更好。通过分析,不难发现这主要源于以下两点:(1)IGA的初始种群质量优于TGA,其可行染色体比例较高,避免大量不满意染色体生成。(2)IGA的局部搜索提高了子代个体向最优解的收敛性。相比TGA,IGA的求解能力更强、更高效。
针对非连通图旅行商路径问题设计了IGA,采用基于旅行商遍历城市次序的编码方式、执行交叉变异操作以及局部邻域搜索操作,解决了TGA在随机方式下生成大量非可行解的问题,加速染色体向最优解收敛,实际案例验证了其求解的高效性。今后的研究可着眼于最优解为非可行解条件下初始种群的再调整,同时设计能向最优解更快收敛的高效IGA。
[1]YANG J H,WU C G,LEE H P,et al.Solving traveling salesman problems using generalized chromosome genetic algorithm[J].Progress in Natural Science,2008,18(7):887-892.
[2]吴春国.广义染色体遗传算法与迭代式最小二乘支持向量机回归算法研究[D].吉林:吉林大学,2006.
[3]黄永青,梁昌勇,张祥德,等.一种小种群自适应遗传算法研究[J].系统工程理论与实践,2005,25(11):92-97.
[4]郏宣耀,王芳.一种改进的小生境遗传算法[J].重庆邮电学院学报(自然科学版),2005,17(16):721-723.
[5]ZHAO X C,GAO X S.Affinity genetic algorithm[J].Journal of Heuristics,2007,13(2):133-150.
[6]BIERWIRTH C,MATTFELD D,KOPFER H.On permutation representations for scheduling problems[C].Proceedings of the 4th International Conference on Parallel Problem Solving from Nature.Berlin,Germany:Springer,1996:310-318.
[7]MURATA T,ISHIBUCHI H,TANAKA H.Genetic algorithms for flowshop scheduling problem[J].Computers&Industrial Engineering,1996,30(4):1061-1071.
[8]汪民乐,高晓光,刘 刚.遗传算法早熟问题的定量分析及其预防策略[J].系统工程与电子技术,2006,28(8):1249-1251.
[9]陶林波,沈建京,韩强.一种解决早熟收敛的自适应遗传算法设计[J].微计算机信息,2006,22(12):268-270.
[10]康立山,谢云,尤矢勇,等.模拟退火算法[M].北京:科学出版社,1994.
