旋转机械故障信号的去噪源分析

王元生，任兴民，杨永锋，邓旺群

（1.西北工业大学 振动工程研究所，西安 710072；2.中国航空动力机械研究所,湖南 株洲 412002）

振动信号是其机械故障特征识别与诊断的重要信息来源，由于机械结构传递特性的影响，实测信号往往是若干个信号的耦合，单从局部频段波形分析信号难以全面理解信号的构成机理。且传感器所获信号常受到未知噪声干扰，给特征识别与诊断带来很大困难。快速有效的对旋转机械进行故障诊断在工程上具有重要意义。

盲源分离(blind source separation，BSS)技术的研究为旋转机械振动信号的分离和故障特征识别提供了条件。去噪源分离(Denoising source separation，DSS)是盲源分离中新的研究热点，根据信号的统计特性，选择不同的去噪函数，从而实现源信息的分析。国外，SÄRELÄ和Valpola[1]详细说明了DSS基本理论和算法原理，并将其应用于分离CDMA信号和脑磁信号。ALMEIDA等[2]通过DSS中的先验理论去噪处理非线性混合图像。CHEVEIGNÉ[3]研究了新的时间变化的DSS方法并应用于处理脑磁电信号，HE等[4]研究了基于最大后验估计的DSS方法并应用于齿轮箱的工程实际中。国内相关的研究较少，成玮等[5]研究了DSS基于不同去噪函数的源分离算法的分离性能，并将其应用于舰艇舱壁混合信号中提取振源的振动特征信息。汤辉等[6]将DSS应用于多个直扩信号参数估计。在此基础上研究DSS基本理论，通过性能指标及相似系数定量比较了与盲源分离的性能优劣，并将其应用于燃气轮机的故障信号中提取振源的振动特征信息，取得了良好效果。

1 盲源分离（BSS）

1.1 BSS理论

在实际应用中，检测到的旋转机械振动信号往往由多个振源信号混叠在一起，含有噪声信号和干扰信号，因此盲源分离的数学模型可以表示为：

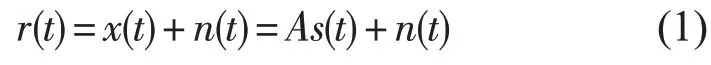
其中，s(t)=[s1(t),...,sn(t)]为n个振源信号构成的n维向量；m×n维矩阵A称为混合矩阵；n(t)为在源信号上叠加的m维噪声干扰信号；r(t)=[r1(t),...,rm(t)]为m维观测数据向量，其元素是各个传感器检测到的旋转机械振动信号。

1.2 Fast ICA

独立分量分析(ICA)是盲源分离的主要方法，它是1997年由芬兰赫尔辛基大学的Hyvärinen等人依据中心极限定理提出的一种固定点算法[7]。之后又对算法进行了简化和改进。作为主要方法Fast ICA依据负熵[8]建立的目标函数为

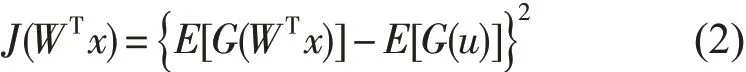
式中，u为一零均值和单位方差的高斯随机向量；G(u)为一任意非二次型函数。

算法的目标就是通过选取W，使负熵J(WTx)最大化，即E[G(WTx)]最大。因此依据式(2)及牛顿迭代原理推导出的Fast ICA基本迭代公式为

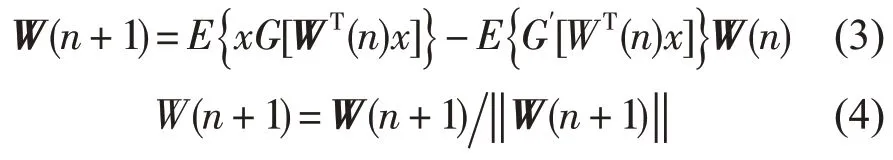
选取初值W，对检测到的振动信号x(t)通过式(3)、式(4)循环迭代至收敛可得到分离矩阵W，进而得到分离量。

2 DSS理论与方法

2.1 DSS理论

期望最大(Expectation maximum，EM)算法[1]是利用最大似然估计方法对信号中丢失的信息进行估计，分成两步骤：(1)在已知的混合信号X和当前估计矩阵A的基础上，通过贝叶斯理论[9]计算源信号S的后验概率；(2)通过新的估计源信号S，更新混合矩阵A。

首先计算概率密度q(S)

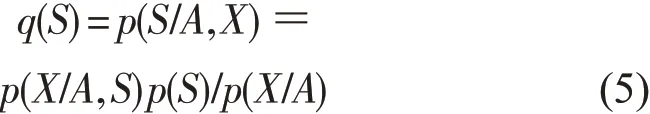
然后寻找混合矩阵新的估计值A

式中后验概率概率密度的协方差为

源信号的噪声估计可写成S=A-1X，

由于对数据的球化和后验概率密度q(s)，因此A-1∞AT，那么源信号的含噪估计为

对于相互独立的源信号，则期望值E[S/X，A]为ATX的函数，即为

那么后验期望可由概率密度分布函数p(S)表示为

式中ε取决于噪声的方差。

通过这种计算方法可得盲源分离的高斯算法，而下面给出的DSS算法将从另外角度去理解去噪函数f(s)。

相对EM算法中的分量被同时求出，在一个相似的推到导算法[7]中，运用预白化的方法逐次提取混合信号的分量，计算如下

在算法中，式(12)计算源信号的噪声估计，W为混合矢量，也为分离矢量；式(13)中通过s+来定义去噪函数；式(14)为重估阶段；式(15)完成归一化。式(13)中去噪函数的选择是DSS[2]的关键。

2.2 谱移动

谱移动技术可以提高DSS算法的收敛速度，定义如下

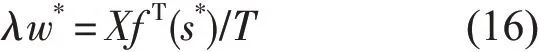
变量S引入函数f(S)中，由于XsT∞W，虽然谱移动不会影响函数固定点，但是影响特征值的速率和加快收敛速度，f(s)从而可被替换为

式中，α(s)和β(s)为信号标量。

由式(16)和式(17)可得出

谱移动通过β(s)来修改特征值的比率，由||[λ1+β(s)]/[λ2+β(s)]|＞|λ1/λ|2可知，这个步骤可以加快收敛的速度。

在采用正切去噪函数[5]中，根据不同源信号，采用两种选择：(1)当源信号为亚高斯时，此时β(s)=0，f(s)=tanh[s(t)]；(2)当源信号为超高斯时，此时β(s)=-1，f(s)=s(t)-tanh[s(t)]。

2.3 评价标准

（1）相似系数

以分离信号yi与源信号sj相关系数作为一个盲分离算法的评价标准。记相似系数εij=ε(yi,sj)，则定义如下

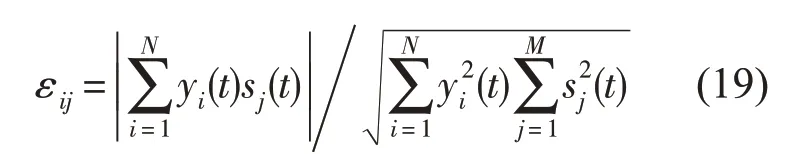
如果εij=1，说明第i个分离输出信号与第j个源信号完全相同，但是由于估计误差不可避免，因此分离完成后的相似系数值只能接近于1；如果相似系数εij趋近于零或者距离较远，则说明分离并未完成。

（2）性能指数

定义一种衡量全局矩阵G对角化程度的度量函数称为PI值(Performance index，PI)

其中gij为全局矩阵G的第i行、第j列元素，n为信号数目。PI(G)值可以合理的从总体上反映全局矩阵G与其常规交互矩阵的近似程度，若G为对角矩阵或其交互矩阵，则其PI(G)值等于零。PI(G)值越小，分离效果越好。

3 仿真分析

旋转机械复合故障信号之间相互耦合，存在振动冲击、碰摩调制和环境噪声等信号。各种信号通过叠加及调制组成复杂信号。传感器的灵敏性，导致环境噪声的影响较大。仿真实验选取四种基本信号S4，S2，S3，S4。设采样频率为1 000 Hz，采样长度为1 000，源信号特征波形生成函数如下

图1为源信号波形及功率谱密度图。图2为混合信号波形图，图3和图4分别为采用DSS理论及盲源分离得到分离后波形及功率谱密度图。

由图3、图4可得，DSS分离后信号与源信号的相关系数最大为0.97，信号的特征得到较好的提取；盲源分离后的信号相关系数最大为0.90，且未能有效的显示源信号的波形信息，分离图形中波形还存在噪声信号。所以，DSS对振动信号噪声抑制效果明显，保留了特征信号，可以较好地从混合的振动信号中分离出激振源信号。

图1 源信号波形及功率谱密度图Fig.1 The original signals and power spectral density(PSD)

PI值越小时说明信号的分离效果越好，实际上当PI值达到10-2时，就表示信号的分离效果已经很好了，由表1可知DSS的信号分离效果更好。

图2 混合信号波形图Fig.2 The mixed signals

图3 DSS分离后波形及功率谱密度图Fig.3 The separated signals and PSD by DSS

表1 性能指标PI值对比Tab.1 The PI value contrast

图4 盲源分离后波形及功率谱密度图Fig.4 The separated signals and PSD by BSS

4 工程应用

燃气轮机[10]是一套结构复杂的旋转机械，其振动信号本质上是各个机械零件振源信号，通过结构传递到表面耦合的复杂混合信号。测试中在某燃气轮机上布置了多个测点，采集了其齿轮箱的振动测试数据为分离对象的多路位移信号(单位为mm)。振动信号通过3个压电加速度传感器采集，分别置于机匣顶部以及输入输出轴承座上。通过检测到机组轴承上的一组故障信号进行分析，采样频率为5 000 Hz，其转子工作转速为10 100 r/min，可以得到如图5所示的源信号图及频谱图，图6和图7分别为采用DSS及盲源分离得到分离后波形及频谱图。

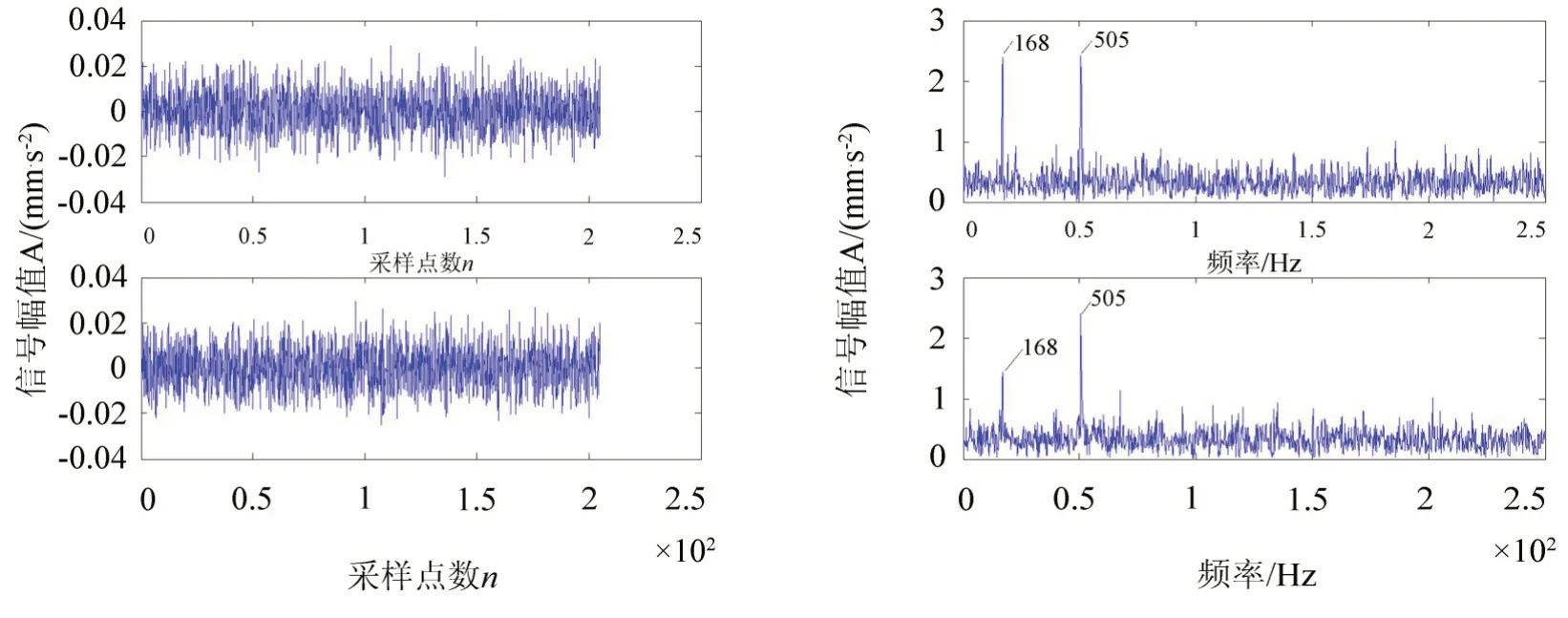
图5 源信号波形及频谱图Fig.5 The original signals and frequency spectrogram

图6 DSS分离后信号波形及频谱图Fig.6 The separated signals and frequency spectrogram by DSS

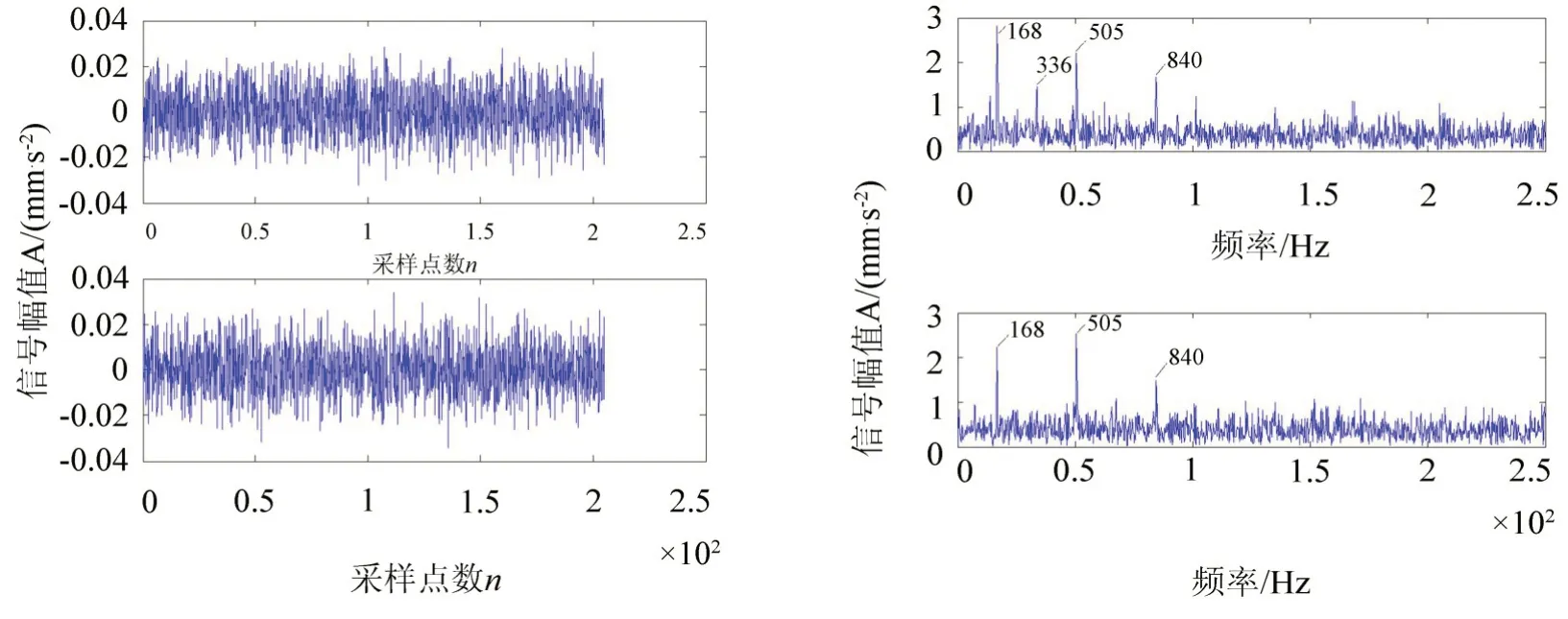
图7 盲源分离后的波形及频谱图Fig.7 The separated signals and frequency spectrogram by BSS

由图5可知，两路信号转子的基频分量都比较突出，可以判断燃气轮机振动过大的主要原因是转子不平衡；图中观测信号中噪声较大，需对信号作进一步分析。

由图6与图7可知，在信号分离之后，转子的振动不仅含有工频信号，还出现了谐波分量、基频、多个倍频等信号，其中3倍频含量很高，可以判断转子出现了可能由局部碰摩引起的异频伪共振现象，与现场监测系统诊断情况[10]相符。转子振动信号中含有大量噪声信号且与特征信号混合在一起，经过去噪源分离后信号降低了噪声和其它随机干扰信号的影响。相比盲分离效果更好，故障诊断的准确性大为提高。

5 结语

分别采用DSS方法和盲源分离方法对仿真信号及某型燃气轮机的故障信号进行分析，并进行分离比较，结果表明：

(1)DSS方法与盲源分离方法相比，DSS方法与源信号的相似系数更高，PI值更小，分离效果更好；

(2)DSS分离方法对旋转机械振源噪声的降低效果良好；有效地提取出转子振动故障信号特征。

[1]SÄRELÄ J，VALPOLA H.Denoising source separation[J].Journal of Machine Learning Research,2005,6:233-272.

[2]ALMEIDA M S C,VALPOLA H,SÄRELÄ J.Separation of nonlinear image mixtures by denoising source Separation[C].Proceedings of the 6th International Conference on Independent Component Analysis and Blind Source Separation，Mar.5-8,Charleston，SC，USA.Berlin,Springer-Verlag,2006:8-16.

[3]CHEVEIGNÉ A.Time-shift denoising source separation[J].Journal of Neuroscience Methods 2010,189:113-120.

[4]HE Q，FENG Z，KONG F.Detection of signal transients using independent component analysis and its application in gearbox condition monitoring[J].Mechanical Systems and Signal Processing,2007,21(5):2056-2071.

[5]成 玮，张周锁，何正嘉.降噪源分离技术及其在机械设备运行信息特征提取中的应用[J].机械工程学报，2010，46(13)：128-134.

[6]汤 辉，王 殊.基于去噪盲分离的多个直扩信号参数估计[J].系统工程与电子技术，2011，33(8)：1722-1726.

[7]HYVARINEN A,HARHUNEN J,OJA E.Independent component analysis[M].New York:John Wiley ＆ Sons Inc,2001.

[8]Chi-Tat Leung,Wan-Chi Siu.A general contrast function based blind source separation method for convolutively mixed independent sources[J].Signal Processing,2007,87(1):107-123.

[9]范 涛，李志农，岳秀廷.基于变分贝叶斯算法和MLP网络的后非线性混合盲源分离方法研究[J].振动与冲击，2010，29(6)：21-24.

[10]凯 旗，任兴民，秦卫阳.燃气轮机发电机组的振动信号监测与分析系统[J].噪声与振动控制，2007，4(2)：40-42.