机械故障诊断的信号处理方法：频域分析

2013-12-05王金福李富才

噪声与振动控制 2013年1期

王金福，李富才

(上海交通大学机械系统与振动国家重点实验室，上海 200240)

频域分析是机械故障诊断中信号处理最重要和最常用的分析方法。工程上所测得的振动信号一般为时域信号，即描述随时间变化的振动信号变化情况。然而由于故障的发生、发展往往引起信号频率结构的变化。例如齿轮箱的齿轮啮合误差，齿面疲劳剥落都会引起周期性的冲击，在时域分析中很难区分，但这些故障在振动信号中就会有对应的频率成分出现。因此，为了通过所测信号了解、观测对象的动态行为，需要分析频域信号。将时域信号变换至频域加以分析的方法，称为频域分析，频谱分析的原理是把复杂的时间历程波形，经傅立叶变换分解为若干单一的谐波分量来研究，以获得信号的频率结构以及各谐波幅值、相位、功率及能量与频率的关系。

1 频域分析

1.1 幅值谱

幅值谱是表征每个频率分量振动幅值大小的频谱图。它是故障诊断中最常用、最直观的分析手段，不平衡相伴生，表现为非线性的振动特征。其振动形式以径向垂直振动为主，激振频率除基频成分外，还伴有高次谐波成分3fr，5fr，7fr及分数谐波成分(0.3～0.5)fr，fr为旋转频率。

幅值谱分析广泛应用于齿轮的故障诊断中。齿轮的振动频谱图的谱线一般有：齿轮的转动频率及其低阶谐频、齿轮的啮合频率及其倍频、啮合频率的边频带和齿轮幅的各阶固有频率等。其中，齿轮副的固有频率是由于齿轮啮合时齿间撞击而引起的齿轮自由衰减振动，它们位于高频区且振幅较小，易被噪声信号淹没。齿轮振动的频谱图包含丰富的信息，不同的振动特点，其相应的谱线发生特定的变化，因而对齿轮各种作状态的频谱进行分析，从中可确定其故障。

不同轴齿轮、局部异常齿轮的时域波形和频谱具有明显的特征[2]，如图1所示。由幅值谱图的变化规律及故障特征频率即可诊断一般性故障类型。

通过对幅值谱的分析可以解决以下问题：

(1)求得振动参数量中的各个频率成分和频率分布的范围；

(2)求出振动参数量中各个频率成分的幅值的大小，从而得到影响设备状态的主要频率值及其对应的幅值大小。

对于特殊的机械设备故障，其幅值谱具有明显的振动频率特征，现场工程师了解这些特征后便可以准确判断机械设备的故障类型，进而进行维修与改善[1]：

(1)转子不平衡：振动的激振频率为单一的旋转频率即工作频率，而无其它倍频成分；

(2)转子不对中：转子不对中是指转子中心与轴承中心不对中或多转子系统中各转子的轴线不对中，其产生原因如下：转子及支座安装不良轴承支座由不均匀膨胀引起变形，地基下沉。

转子不对中相当于在联轴器端输入某种激励，对刚性联轴器及齿轮联轴器，其径向激振频率除旋转频率fr由角度不对中引起外，主要以旋转频率的二倍频或四倍频为主，且伴有高次倍频n·fr(n=6，8……)。轴向振动频谱由基频及其谐波组成，基频具有峰值；

(3)基座或装配松动：基座或装配松动常和转子

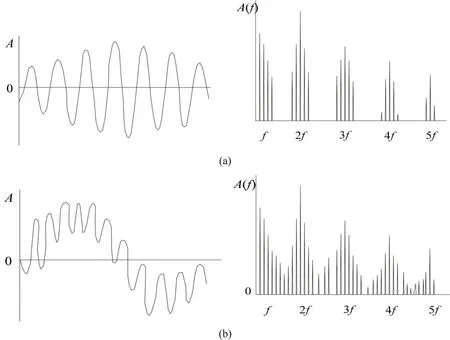
图1 不同故障齿轮时域波形和频谱对比：(a)不同轴齿轮的时域波形和频谱；(b)局部异常齿轮的时域波形和频谱Fig.1 Waveforms and spectrums of different gear faults

频谱分析技术同样广泛应用于具有明显特征的NVH现象（Noise，Vibration and Harshness，噪声、振动、声振粗糙度）的汽车故障诊断[3]，煤气鼓风机、增压鼓风机增速箱振动[4]、发电机转子[5]等旋转机械的故障诊断。对于机械设备的故障诊断，除了必要的设备故障诊断仪器及专家系统等处理软件，工程技术人员还必须掌握相当高的设备故障诊断专业知识，具有丰富的解决机械故障的实践经验，二者结合起来才能及时消除设备故障。总结不同故障的振动信号特征能够为现场工程师提供必要的参考，丰富其经验，保证故障诊断的可靠性。

1.2 功率谱

功率谱反映了随机信号各频率成份功率能量的分布情况，可以揭示信号中隐含的周期性及靠得很近的谱峰等有用信息，应用极其广泛，例如，在语音信号识别、雷达杂波分析、地震勘探信号处理、水声信号处理、系统辨识中非线性系统识别、物理光学中透镜干涉、流体力学的内波分析、太阳黑子活动周期研究等许多领域发挥了重要作用。

对于机械设备各种特征频率的确定是对设备进行故障诊断的基础，当机械设备发生故障时；多般在某些特征频率附近出现明显的峰值，功率谱是反映各频率成分能量分布的关系，更容易得到峰值出现位置处所对应的频率，与设备特征频率进行对比分析，便可得到设备的故障类型。

实际应用中的平稳随机信号通常是有限长的，只能根据有限长信号估计原信号的真实功率谱，这就是功率谱估计。

功率谱估计分为经典谱估计和现代谱估计。经典谱估计是将数据工作区外的未知数据假设为零，相当于数据加窗，主要方法有相关法和周期图法。现代谱估计是通过观测数据估计参数模型再按照求参数模型输出功率的方法估计信号功率谱，主要是针对经典谱估计的分辨率低和方差性能不好等问题提出的，应用最广的是AR参数模型[6]。

功率谱估计中的相关函数法和周期图法所得到的结果是一致的，其特点是离散性大，曲线粗糙，方差较大，但是分辨率较高。现代谱估计方法曲线比经典谱估计方法光滑，其处理结果的方差也要比经典谱估计方法处理的结果小。

当数据长度长，谱分辨率高，现代功率谱估计与经典功率谱估计的选取对分析结果影响不大；对一组冲击数据进行谱估计，由于冲击振动的特点，时间短，所以振动峰值的数据点数很少。用经典功率谱估计，得到的频率分辨很低，容易造成谱形奇变；用现AR参数模型估计，频率分辨率不受数据长短的限制，谱形真实。经典法频率分辨率低，谱线偏移较为严重；现代谱估计的频率分辨率高，精度高，在冲击信号分析处理中的应用广泛。

在工程设计中，根据经验，短数据如冲击谱分析，用经典功率谱估计不合适，采用现代AR模型比较合适，阶次的选取在一般为数据长度的1/6～1/5；长数据如振动谱分析用经典功率谱比较合适[7]。

以功率谱分析法在泵轴承故障监测中的应用[8]为例。

泵既有齿轮的回转运动，又有曲轴连杆的往复运动。这对于把振动检测技术运用到其它机械传动装置的故障监测，将有很好的借鉴作用。泵测点布置遵循最靠近振源、界面最少原则。

啮合频率459 Hz以下有两个谱强度很高的振动179 Hz和300 Hz。按理论计算，在啮频以下只有轴承的特征频率。所以，这两个谱峰应该是小齿轮轴承滚道缺陷所致。

该泵各测点啮频谱强度并不高，但是啮频以下在169～250 Hz有两个谱强度较高的振动，而以3、4两测点为最高，这都与该处小齿轮轴大机壳一侧轴承的特征频率内滚道缺陷237 Hz、外滚道缺陷179 Hz是相一致的。

功率谱分析通常也与其他信号处理方法综合应用于机械设备的故障诊断中，其中经验模态分解（EMD）结合功率谱方法相结合，在轴承故障诊断中，对于滚动体故障、外圈故障等不同的故障类型，在IMF功率谱曲线中，与故障特征频率近似集合的频率处具有明显的峰值，取得了很好的分析效果[9]。

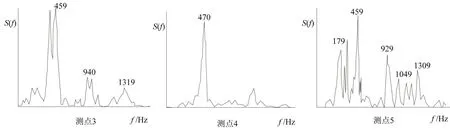
图2 轴承点蚀剥落的典型图谱Fig.2 Spectrum of the corrosive pitting

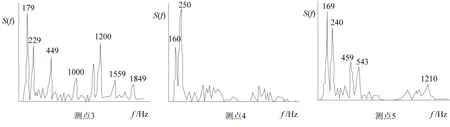
图3 轴承表面凹坑的典型图谱Fig.3 Spectrum of the surface cavity

测量噪声频谱、检验埋没在宽带噪声中的窄带信号，飞行器实测数据的分析，以及用噪声激励法估计线性系统的参数等，都要应用到功率谱估计。因此，随机信号的功率谱估计是当前信号处理中的一个重要的研究课题。在经典功率谱的基础上出现了功率谱熵、矢功率谱很多新的功率谱分析方法，在机械设备故障诊断中同样发挥着不容忽视的作用[10，11]。

1.3 倒频谱

倒谱变换主要有两种分析方法：复倒谱分析和实倒谱分析。复倒谱分析保留了信号的全部信息，能够对信号的回声进行检测；实倒谱分析则在变换过程中保留了信号的频谱幅度信息，摒弃了相位信息，所以不能够对信号进行重建，但是可以利用它来进行重建一个最小相位信号[12]。

倒频谱分析具有极强的信号识别功能，能较好地检测功率谱上的周期成分。通常在功率谱上无法对边频的总体水平做出定量估计，而倒频谱对边频成分具有“概括”能力，能够将原来谱上成簇的边频带谱线简化为单根谱线，可以检测出功率谱中难以辨识的周期性信号[13]。

倒频谱与自相关函数有着密切的关系

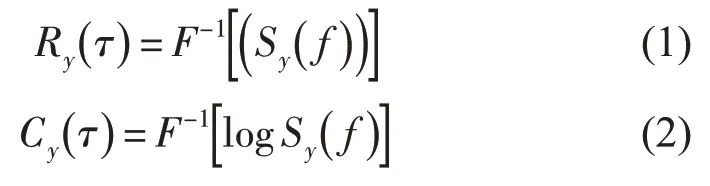
Ry(τ)为信号自相关函数，Cy(τ)为信号倒频谱，Sy(f)为信号的自功率谱。倒频谱与自相关函数的不同之处在于对数加权。对数加权的目的在于使再变换以后的信号能量格外集中，从而使谱线定位准确、幅值突出；可以分开卷积积分，易于识别源信号或系统特性（前者在高倒频区，后者在低倒频区）；对于频域调制信号，频率的边带族成分能较好的分辨出来。这三条正好弥补了常规谱分析的不足之处[14]。

机械设备在故障运行时，故障信息对运行信号起调剂作用，在频谱中形成一系列的边频带。这种边频族，在倒频谱中反映为相应的“倒谱峰”。倒谱峰对应的“倒频率”则代表调剂周期，其倒数则为调剂频率。因此，需要强调的是，“倒频率”仅与频率间距有关，与绝对频率无关。特别是在往复泵的故障诊断过程中，由于其特有的二次不平衡力和不平衡力矩的原因，在功率谱和倒频谱图中，在齿轮啮合频率及其倍频附近可能各存在某一边频成分[15]。

在齿轮箱的故障诊断中，关键是对齿轮的状态检测和故障诊断。齿轮箱工作时所产生的振动信号含有齿轮加工、安装、运行及损伤状态等信息，所以齿轮故障的诊断关键是如何把各种有用的故障信息分离出来。

当齿轮出现故障，故障齿轮的振动信号往往表现为回转频率对啮合频率及其倍频的调制，在谱图上形成以啮合频率为中心，两个等间隔分布的边频带。由于调频和调幅的共同作用，最后形成的频谱表现为以啮合频率及其各次谐波为中心的一系列边频带群，边频带反映了故障源信息，边频带的间隔反映了故障源的频率，幅值的变化反映了故障的程度。因此，齿轮故障诊断实质上是对边频带的识别。特别是在带偏心误差的齿轮中，同时受到由齿轮运动快慢引起的频率调制及由齿而负载波动引起的幅值调制，使频谱更为复杂。利用倒谱分析可把边带信号分离出来，使在功率谱中难以分辨的周期分量在倒谱图中变为离散的线谱，其高度反映了原功率谱中的周期分量的大小，极易识别其变化和特点。因此，倒频谱分析方法在齿轮箱的故障诊断过程中经常应用。

倒频谱分析在齿轮箱故障诊断中的优越性[16]：

(1)倒频谱变换受传输途径的影响很小

振源和传递途径的影响表现为倒频谱的相加。由于振源与传递途径的倒频谱相互差别很大，它们在倒谱中是分开的，很容易区分出来。这一结果也表明用倒频谱来诊断故障信号时，测量位置的选择要求不是很严格；

(2)倒频谱是一种再现的频谱，它能分析出复杂频谱图上的周期结构，分离和提取频谱中的周期成分；

(3)倒频谱变换能在整个功率谱范围内求取边频带的平均间距，因而既不会漏掉边频信号，又能给出非常精确的间距结果。倒频率值的倒数则为故障信号的频率。

对于倒频谱分析方法，以下以电动机齿轮传动箱倒频谱分析为例描述其诊断过程。

当倒频率峰值处对应频率接近齿轮转动频率时，可推断功率谱中的边频带主要由对应转轴调制而成，说明故障发生在齿轮上，可能发生磨损、点蚀、剥落等故障；当出现轴频及其转动频率的倍频时，说明对应轴可能有不对中或不平衡故障，当倒频率峰值处对应轴承内圈转动频率时表明轴承内圈存在故障。

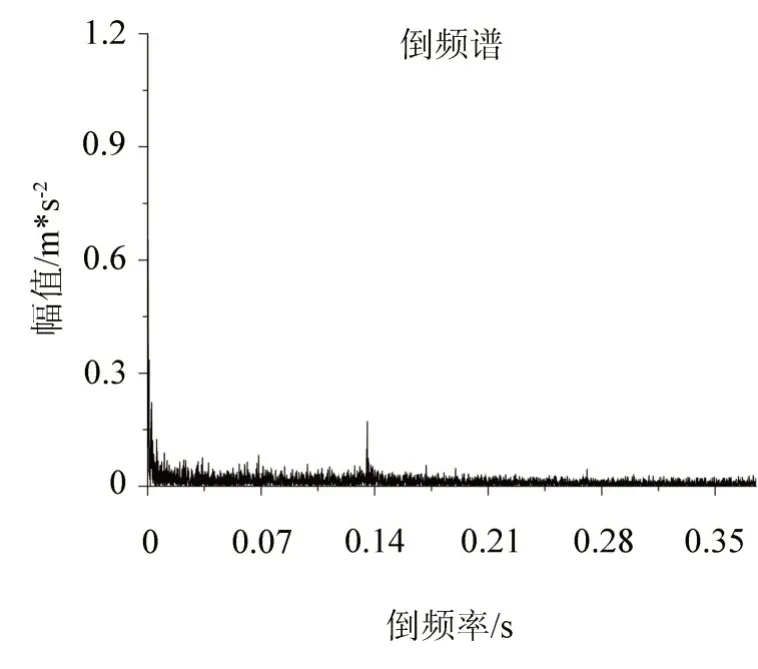
图4 电动机正常状态下振动信号的倒频谱Fig.4 Cepstrum of electric motor in normal condition

以下再以电动机齿轮箱倒频谱分析结果为例。

图5中在181.2 ms处出现峰值，对应频率f=1/τ=1 000/181.2=5.52 Hz，与轴承内圈转动频率十分接近，可推断故障发生在轴承内圈位置。

应用倒频谱进行齿轮故障诊断，首先计算齿轮传动箱的轴频、啮合频率等特征频率，计算倒频谱图中出现倒频率峰值位置所对应频率，与特征频率进行比较，确定故障类型与位置。

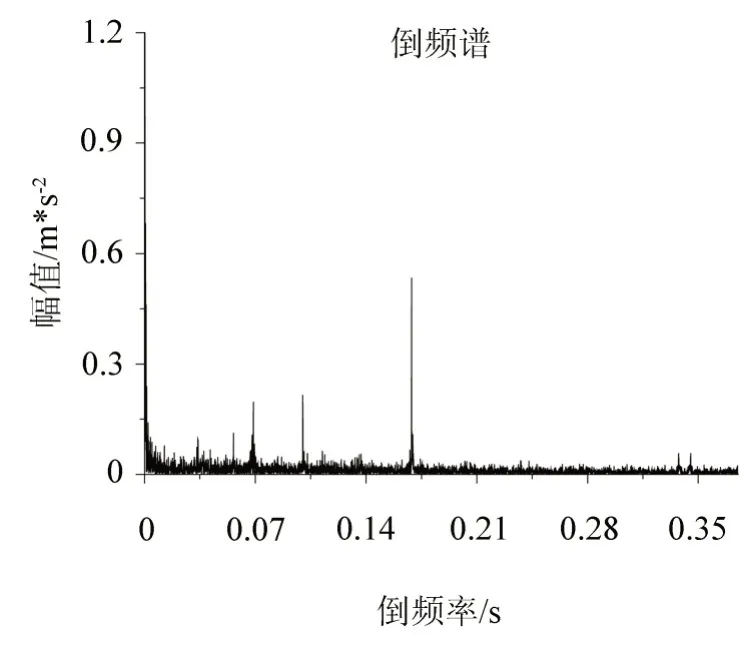
图5 电动机轴承内圈出现故障时振动信号倒频谱Fig.5 Cepstrum of inner circle fault

倒频谱分析广泛应用于液压泵早期故障诊断、航空发动机的各类旋转机械的故障中[17]。

在对液压泵进行早期故障诊断的过程中，由于振动信号的倒频谱对轴向柱塞泵发生早期松靴故障（轻微松靴故障）敏感[18]，通过对正常泵与故障泵振动信号倒频谱的对比分析可发现，故障泵在转轴基倒频率的二次谐波上的幅值明显大于正常泵的幅值。

对于转子不平衡、半速涡动及油膜振荡、转子不对中、共振、部件松动、转子与定子摩擦、转子结构缺陷与裂纹、轴承缺陷等故障都反映在振动信号谱图的相应频率分量上，即都有其特殊的故障征兆。这些征兆有1/3倍频、1/2倍频、工频、2倍频、3倍频等[19]。

在倒频谱的谱线中有些找不到对应目标的，则有可能产生构件动特性因素，要彻底了解它们，应对结构做模态分析。另外，用倒频谱分析法诊断出的故障现象，并不等于这些故障已达到不可允许的程度，某些情况下它们只反映了有关部件制造或安装的标准不高而已，因此，我们也可以用倒谱来检验产品质量，制定检验标准[20]。

倒频谱分析方法还可以与小波分解、频谱细化技术、希尔伯特变换解包络等其他信号处理方法相结合达到故障诊断的目的。例如，故障特征频率较低时，先利用小波分解将检测信号频率细分到不同频段中消除干扰；然后采用倒频谱分析方法将故障特征信号变换为单根的峰值谱线，根据峰值谱线的时间周期，求得故障特征频率，并确定各故障类型[21－23]。

1.4 细化谱

由于计算机只能对有限多个样本进行运算，FFT和谱分析也只能在有限区间内进行，这就不可避免地存在由于时域截断产生的能量泄漏，使谱峰值变小精度降低，即经FFT得到的离散频谱其幅值相位和频率都可能产生较大的误差，从理论上分析，加矩形窗时单谐波频率的最大误差可达36.4%，即使加其它窗时，也不能完全消除此影响，如加Hanning窗时，只进行幅值恢复时的最大误差仍高达15.3%，相位误差高达90 rad。因此，频谱分析的结果在许多领域只能定性而不能精确的定量分析和解决问题，大大限制了该技术的工程应用[24]。

频谱的细化分析技术就是对感兴趣的重点频率区域进行放大，得到较高的频率分辨率，得到更加精确地频谱幅值，相位和频率。频率细化的方法很多，常用有ZFFT(复调制细化)分析方法和相位补偿ZFFT方法[25，26]。

应用细化谱分析技术，多建立在在分析幅值谱、了解信号的频率组成的基础上，为了得到更加精确的幅值、相位等信息，对感兴趣的频率区间进行频谱的细化，从而更加准确的判断故障类型与故障发生程度的大小。

以下再举仿真信号

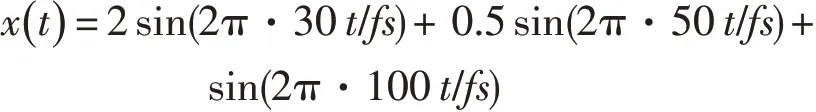
的分析为例

由图6(a)得出信号包含30 Hz的频率成分，选取10 Hz～40 Hz为细化区间，得到细化谱图6(b)，可以看出图6(b)中30 Hz的频率成分的频率和幅值在细化谱中得到了更加精确的值。对于机械设备的故障诊断，现场工程师可利用同样方法得到振动信号的细化谱，为判断故障类型和故障程度大小提供更为准确的依据。

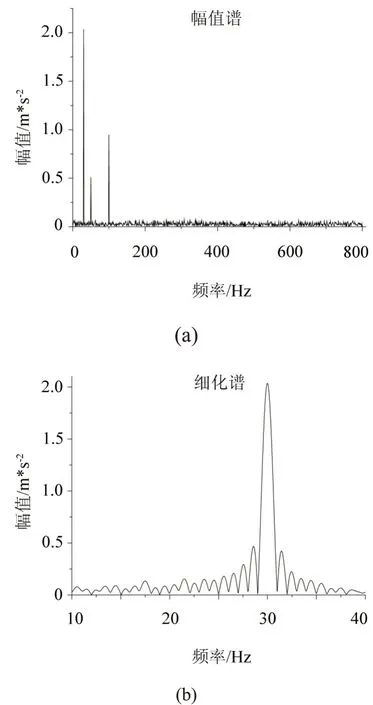
图6 仿真信号的细化谱 (a)仿真信号幅值谱；(b)10 Hz～40 Hz区间内的细化谱Fig.6 Thinning spectrum of analogue flow signal

1.5 希尔伯特解调

一个实信号x(t)的希尔伯特变换定义为

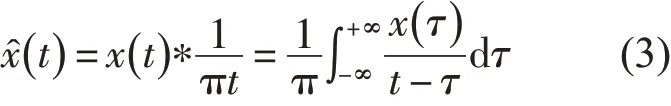
于是得到x(t)的解析信号

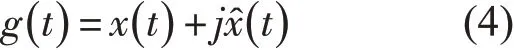
g(t)的幅值

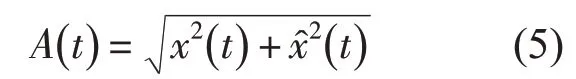
便是原始实信号x(t)的包络。

解析信号g(t)的瞬时相位φ(t)定义为φ(t)=tan-1(t)x(t)]；很自然，解析信号g(t)的瞬时频率f(t)就定义为f(t)=(2 π)-1[dφ(t)dt]。

机械设备故障，尤其是齿轮箱的故障，如齿轮断齿、点蚀、滚动轴承的疲劳剥落、轴弯曲等，都会产生周期性的脉冲冲击力，产生振动信号的调制现象，在频谱上表现为在啮合频率或固有频率两侧出现间隔均匀的调制边频带，谱峰较多，难以识别故障。从信号中提取调制信息，分析其强度和频次就可以判断零件损伤的程度和部位，是机械故障诊断中广泛使用的一种分析零件损伤类故障的有效方法，在实践中解决了不少故障诊断方面的问题。

由于加速度计检测出的振动信号幅值与频率的平方成正比，所以幅值谱的分析结果中，低频的调制信号几乎看不到，而高频的振动突出，谱峰及边带密集，振动分析困难。经过解调分析和包络线谱分析后，谱线简明，由转速频率引起的振动信号即调制信号，很容易判断出来，有利于机械设备的故障诊断[27]。

表1 希尔伯特变换对于不同的原始信号解调结果Tab.1 Demodulation of different original signal

希尔伯特变换由于其特点有不少应用领域，例如：对平稳随机信号相关函数的估计；对非频变波传播问题的研究；对幅值调制信号的解调等等。

希尔伯特变换的一个最主要的应用就是处理带通信号的解调。

由于实测信号中，除了所需的调制信号以外，还存在着大量的其它成份信号和噪声信号，其结果影响信号处理效果，严重时甚至失效。因此调制信号在作希尔伯特变换之前，根据信号的来源需作相应的预处理。

(1)同步估号平均

(2)锁相平均

(3)带通滤波：以轴承故障诊断为例，选用轴承结构共振的高频振动信号去进行解调处理，解调处理之前所采用的滤波为带通数字滤波器。由于电机规格不同，使用的轴承型号也不同，其一阶径向固有振动也不同，故带通数字滤波器上、下限频率是可选的。诊断电动机转子故障时利用的是电流的低频信号，对于100 Hz以上的电流谐波为无用的成分，可选用低通滤波器将它滤去。因此，应用希尔伯特变换进行设备故障诊断之前，要根据诊断对象来选用滤波器[28]。

应用希尔伯特变换对机械设备进行故障诊断的实例总结如下

(1)齿轮疲劳裂纹诊断

齿轮的某一齿出现疲劳裂纹时，它的局部刚度下降，齿轮的啮合振动将产生突变的相位延迟，这一特征对早期和扩展的齿轮疲劳裂纹诊断较为灵敏，结合参考信号与相位突跳位置，可以确定裂纹的位置所在，如图7所示；

图7 裂纹齿轮相位特征：(a)早期裂纹振动相位； (b)扩展裂纹振动相位Fig.7 Phase feature of crack gear

(2)联轴节松动诊断

刚性联轴节的松动引起传动系统的扭转刚度下降，其结果为扭振的幅度增加，扭振频率下跌。在重载下这一现象显得更加严重。

对于齿轮转动系统，扭振信号被调制在齿轮啮合振动相位之中。从齿轮箱体拾取的振动信号，经过带通滤波，同步平均和解调即可获得扭振信号。在正常时振动信号的相位基本平直；在松动时，时域相位信号低频谐波成份骤增。值得注意的是：当传动系统中的刚性联轴节松动时，齿轮箱体上所拾得的振动信号从幅值来衡量并没有明显变化，刚性联轴节的松动对传动系统来说较为敏感的特征量是相位信号[29]；

(3)电机特定故障的诊断

电机转子不平衡使转子呈弓形旋转，从而形成转子对定子的动偏心，由动偏心产生的旋转磁拉力引起电动机产生相应的振动，其振动信号为调制形式的振动波形；由绕组谐波电磁场产生电磁力引起相应的振动，也具有调制形式的振动波形。

希尔伯特变换并不是万能的，对低速旋转齿轮、滚动轴承的诊断，解调分析效果良好；对高速旋转齿轮、滚动轴承因其含有其它旋转件的特征频率信号，使解调方法特别受局限。此时最好进行带通滤波后再对信号进行解调分析，并要注意是否有混频现象发生[30]。

希尔伯特变换与其他信号处理方法相结合，也广泛应用与机械设备故障诊断中。基于EMD的希尔伯特变换信号分析方法，既适合于线性信号的时频分析，又适合于非线性信号的分析[31]；希尔伯特变换和小波包节点能量法相结合对齿轮箱故障诊断也收到了很好的效果[32]。

表2 不同故障情况下的调制特点Tab 2.Modulation feature of different fault

能量算子解调作为解调调幅调频信号的另一种方法，与希尔伯特解调有相似的应用。

能量算子是Teager在研究非线性语音建模时引入的一个非常简单的数学算法：设有信号x(t)，则其能量算子定义为[33]

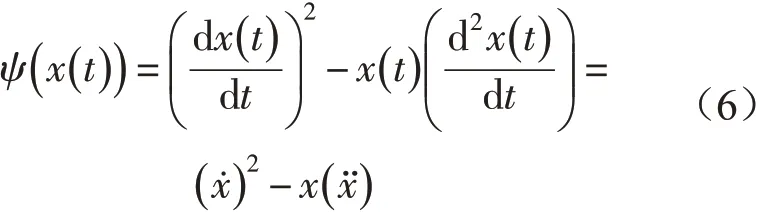
能量算子解调法用于分析和跟踪窄带信号的能量，具有解调精度高、响应速度快等优点，不仅可以用于窄带单个AM（调幅）、FM（调频）信号的解调，还可与用于宽带的多个AM、FM信号组合的解调，对于对比分析不同类型信号具有重要意义[34]。

2 结语

频域分析能够得到信号的频率成分，得到各频率成分幅值、相位等信息，根据故障特征频率对故障类型进行判断，在机械设备故障诊断过程中有极其广泛的应用。本文从频域分析出发，总结了多种信号处理方法的优缺点，以实例说明其在机械设备故障诊断过程中的分析原理，介绍了各种信号处理方法的应用范围及在应用过程中的注意事项。工程技术人员和现场工程师在对具体的机械设备关键构件进行故障诊断过程中，容易掌握频域分析中各种信号处理方法的原理与特点，将理论与工程实际密切地结合，为各行业进行机械设备故障诊断带来方便。

对于各类机械设备故障特征及最优信号处理方法选取的总结，对工程技术人员和现场工程师而言具有很大的指导意义和参考价值。

[1]李敏，等.旋转机械频谱分析及故障诊断[J].梅山科技，2003，3：10-12.

[2]张千锋，等.基于Lab VIEW和RMS幅值谱的齿轮故障诊断[J].机电产品开发与创新，2008，1：90-92.

[3]金岩，常志权.频谱分析技术在车辆NVH故障诊断中的应用[J].噪声与振动控制，2011，1：110-113.

[4]潘高峰.增压鼓风机增速箱振动故障的频谱分析[J].风机技术，2011，3：75-77.

[5]周政新，等.基于频谱分析的发电机转子系统故障诊断[J].电子测量技术，2011，2：80-83.

[6]宋宁.经典功率谱估计及其仿真[J].现代电子技术，2008，11：159-162.

[7]干昌浩.随机振动功率谱估计方法研究[J].中国高新技术企业，2010，12：21-23.

[8]张文，毕庆霞.功率谱分析法在泵轴承故障监测中的应用[J].中国矿业，2007，6：56-59.

[9]张秀峰.经验模态分解结合功率谱方法在轴承故障诊断中的应用[J].机械工程师，2010，12：23-26.

[10]李凌均.矢功率谱与支持向量数据描述相结合在故障诊断中的应用研究[J].机械设计与制造，2011，1：91-93.

[11]费成巍.转子振动故障的过程功率谱熵特征分析与定量诊断[J].航空发动机，2011，1：48-51.