基于模糊PID算法的双侧电传动履带车辆转向控制策略研究

陈泽宇 赵广耀 翟 丽 周淑文

1.东北大学，沈阳，110819 2.北京理工大学，北京，100081

0 引言

履带车辆凭借良好的通过性和越野机动性而广泛应用于农业、矿业和建筑类等工程机械以及军用车辆领域［1］，尤其是近年来电传动系统在履带车辆上的应用进一步推动了履带车辆的迅速发展。电传动履带车辆不仅可以实现更为优越的动力性，而且具有节能、环保的优点，是地面工程车辆发展的重要趋势之一［2］。

转向控制是履带车辆动力学控制的核心内容，也是电传动履带车辆研发过程中的重要环节。转向性能一直是传统履带车辆相比于轮式车辆的明显不足之处，由于不具备前轮转向功能，履带车辆必须通过内外侧履带的差动来实现转向，转向过程中需要克服两侧履带与地面的侧向阻力，能量损耗较大，而且转向轨迹不容易精确控制。要使电传动履带车辆实现良好的转向轨迹，提高车辆转向性能，双电机之间的协同控制策略［3-6］的设计是关键。电传动履带车辆的双侧履带作用力由双侧电机直接控制，因此可以通过综合控制器独立地调节两侧电机状态来灵活地控制双侧履带作用力，如果在转向过程中，综合控制器能够根据转向动力学需求精确合理地分配两侧电机力矩，则可以改善履带车辆转向轨迹控制效果。

针对上述问题，本文首先分析了履带车辆的转向特性，进而提出一种基于模糊PID算法的双侧电机力矩控制策略，使履带车辆实现稳定的转向轨迹并提高转向过程中的横摆角速度动态响应能力；最后基于MATLAB／Simulink建立了转向控制系统仿真模型，对控制策略进行仿真验证和评价。

1 履带车辆转向特性分析

1.1 转向动力学模型

履带车辆的转向方式是一种差动转向，为了便于问题分析，假设地面附着系数与阻力系数均为定常数、内外侧履带垂直载荷分布均匀、忽略离心力导致的垂直载荷二次分布，且忽略履带与地面之间纵向滑移与滑转，其转向动力学模型如图1所示。转向过程中综合控制器控制电机使两侧的履带产生不同的作用力，从而使车辆获得横摆力矩。在横摆力矩的作用下，两侧履带克服与地面之间的侧向阻力，使履带车辆获得横摆加速度。图中Fd1与Fd2表示两侧履带的驱动力，Fr1与Fr2表示两侧履带的滚动阻力，Fr3表示空气阻力，L为履带接地长度，B为两侧履带中心距，u为车辆纵向速度，Fs为地面对履带的侧向阻力，根据转向模型建立平衡方程如下：

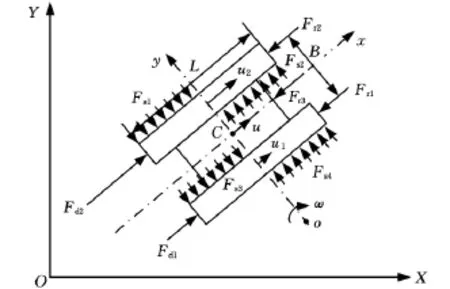
图1 履带车辆转向动力学模型

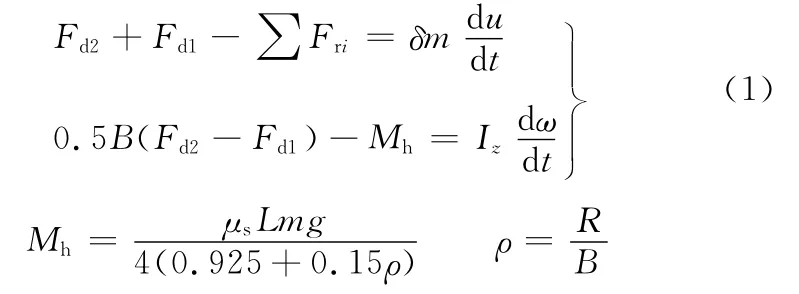
式中，m为整车质量，kg；δ为旋转质量系数；Iz为转向时的整车转动惯量，kg·m2；ω为横摆角速度，rad／s；R 为转向半径，m；Mh为侧向力所产生的横摆阻力矩，是转向半径的函数，N·m；μs为转向阻力系数；ρ为相对转向半径。

履带车辆的转向阻力矩较大，因此在转向过程中通常需要制动内侧履带，令FB＝-Fd1表示内侧履带的制动力，代入式（1）得转向过程中转向半径的表达式为

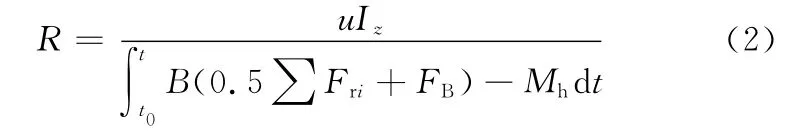
式中，t0为进入转向阶段的时间；t为积分时间。

当履带车辆转向过程达到稳态之后，转向半径、车速和横摆角速度均保持为恒定，式（2）中的分母将不再随时间变化，且根据车速变化率为零，从而可以得出转向进入稳态过程之后内外侧履带作用力之间的关系以及内侧履带制动力与转向半径之间的关系：

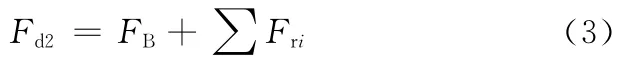
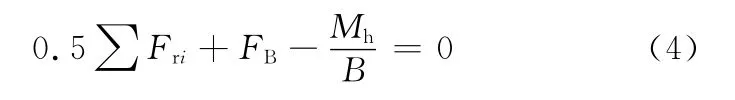
1.2 转向瞬态动力学分析

上述分析过程是在稳态情况下进行的，没有考虑车辆由直驶进入稳态转向之间的瞬态过程。对于直驶中的履带车辆，给定任意转向盘角阶跃输入信号，由于转向半径不可能突变，所以转向初期R接近于无穷大，根据式（1）可知此时Mh接近于0，因此必然有如下关系成立：

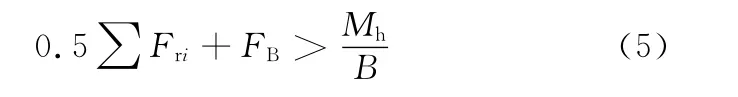
将式（5）代入式（2）可以看出随着时间t的增加，R将逐渐减小，Mh逐渐增大，当Mh增大到Mh＝B（0.5∑Fri＋FB）之后，R达到稳态，不再继续减小，整个过程中转向半径变化如图2所示。

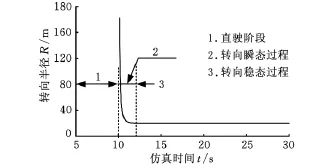
图2 转向盘角阶跃输入下转向半径响应曲线

将驾驶员给出转向盘转角信号之后，履带车辆从直驶进入稳态转向阶段之间所耗费的时间定义为转向动态响应时间td，即图2中第2阶段所需的时间。td主要由三部分组成：驾驶员反应时间、电机动态响应时间和在电机作用力影响下双侧履带克服地面阻力形成横摆角速度的时间。本文重点研究转向控制策略，因此忽略驾驶员反应时间和电机自身的响应时间，结合式（1）～ 式（4）可得转向动态响应时间td与内外侧履带作用力之间的关系：

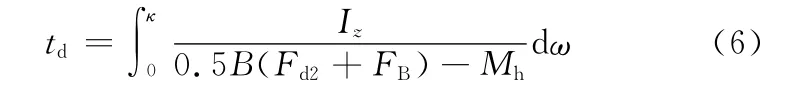
式中，κ为稳态时的横摆角速度，rad／s，由内外侧电机力矩控制与纵向车速确定。

2 履带车辆双侧电传动系统

履带车辆双侧电传动系统通过两个电机独立驱动双侧履带来实现车辆驱动，由发动机发电机组与锂离子动力电池组并联组成车载电源系统，结构简单、控制灵活，是目前履带车辆中应用最为广泛的电传动结构，其系统总成如图3所示。综合控制器接收双侧电机转速反馈信号和驾驶员输入信号，根据转向动力学控制策略确定双电机目标力矩，并将目标力矩通过CAN总线与双侧电机控制器通信。电机控制器实时地对电机进行力矩调节，其作用是使电机实际输出力矩与综合控制器发出的目标力矩值一致。

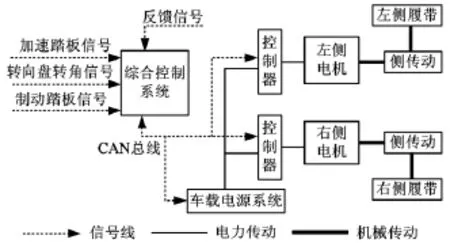
图3 双侧电传动履带车辆驱动系统结构简图

双侧电传动履带车辆的基本参数和设计指标如表1和表2所示。经过匹配计算，电机的峰值功率取为650kW，最大扭矩为2200N·m，最高转速为7500r／min。

表1 设计指标

表2 整车基本参数

履带作用力可以通过电机输出力矩计算，转向时内外侧履带作用力与双侧电机力矩之间的关系如下：

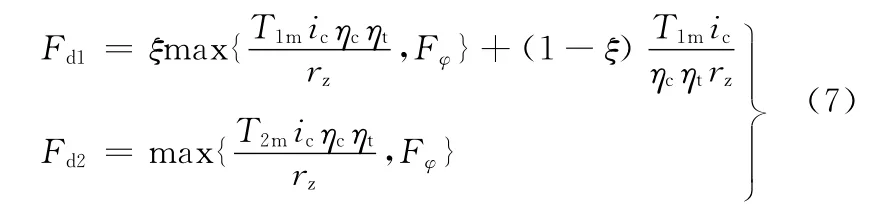
式中，T1m、T2m分别为转向过程中内外侧电机的输出力矩，N·m；Fφ为单侧履带的地面附着力，N；ic为侧传动比；rz为主动轮半径，m；ηc为侧传动效率；ηt为履带效率；ξ为表征内侧履带制动状态的系数。

3 转向控制策略设计

图4所示为双侧电传动履带车辆转向控制策略流程。转向控制策略设计的关键是将转向盘输入信号解释为两侧电机的控制指令，使车辆正确体现驾驶员转向意图，结合履带车辆转向动力学分析，根据式（1）～式（4）可得稳态过程中的转向半径：

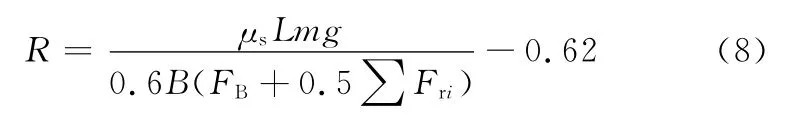
可以看出当履带车辆转向过程达到稳态之后，假设外部阻力为常数，则转向半径R只与内侧履带的制动力有关。因此可以首先将驾驶员转向盘转角信号解释为内侧电机制动力矩，如：

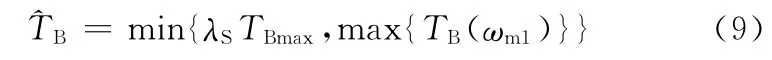
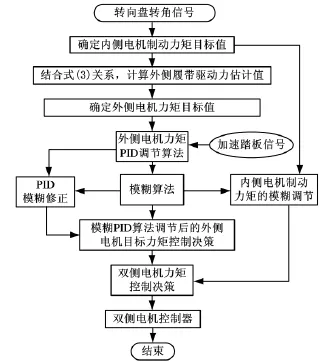
图4 模糊PID转向控制策略流程图

式中，TBmax为内侧电机最大制动力矩，N·m；＾表示估计值；ωm1为内侧电机转速，r／min；max｛TB（ωm1）｝为当前电机转速下的最大制动力矩，N·m；λS为转向盘转角输入信号。

转向盘转角信号定义如下：

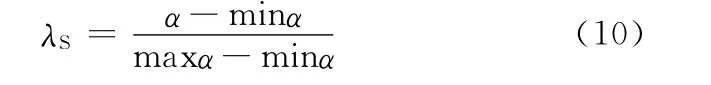
式中，α为转向盘转角，rad；max｛α｝、min｛α｝分别表示转向盘最大转角与自行行程转角，符号规定为向右转向为正，向左转向为负。

在确定内侧电机目标力矩之后，进而对外侧电机采用力矩跟随控制，根据式（3）所示的内外侧履带作用力关系和式（7）所示的电机力矩与履带作用力关系，可得外侧电机力矩估计值：

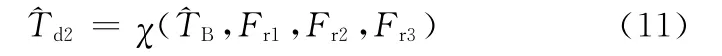
上述力矩分配策略可以实现驾驶员输入信号对稳态转向半径的控制，但是由于履带车辆转动惯量较大，不可避免地存在一个时间相对较长的转向瞬态过程，如果动态响应时间过长，甚至有可能在车辆的转向过程已经结束时转向仍然没有进入稳态阶段，致使实际过程中转向轨迹无法被驾驶员精确控制。可见除了正确地分配两侧电机力矩之外，通过合理的控制缩短转向动态响应时间，使转向尽早进入可控的稳态阶段是改善履带车辆转向轨迹可控性的有效途径之一。

通过式（6）分析可知，当其他参数一定时，如果提高外侧电机力矩Td2便可以有效地缩短动态响应时间，从而使转向尽快进入稳态阶段，但是需要在瞬态过程即将结束时将Td2恢复至目标值，以确保实现正确的稳态转向半径。

3.1 模糊控制策略

为了实现上述控制目标，采用模糊控制策略来完成外侧电机目标力矩的动态调节。模糊控制器采用两输入单输出的Mandani模糊结构，模糊输入为转向半径R及其变化率，模糊输出为力矩调节系数x，模糊输入与模糊输出的隶属度函数如图5所示。

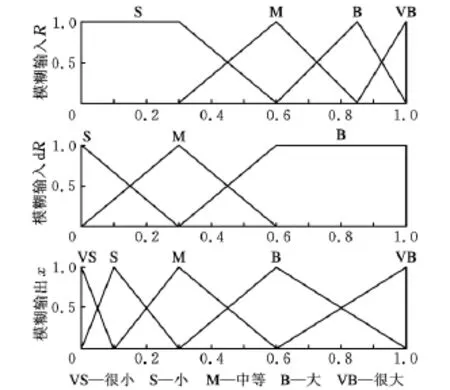
图5 模糊输入与输出变量隶属度

模糊控制规则根据模糊输入来实时地进行外侧电机力矩调节，其控制思路为：如果R越大且dR也越大，则说明车辆正处于转向初始阶段，给外侧电机力矩Td2施加越大的一个调节量，增加Td2；反之如果R越小，dR也越小，则越说明转向瞬态过程即将结束，越缩小Td2调节量，将其恢复至力矩分配策略目标值。根据模糊输入隶属度一共可以建立12条模糊规则，模糊规则的形式为

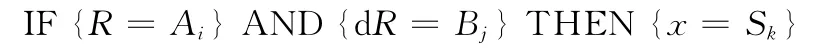
确定了模糊输出系数之后，外侧电机目标力矩为

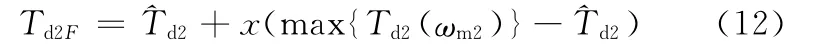
式中，ωm2为外侧电机转速，rad／s；max｛Td2（ωm2）｝为当前转速下外侧电机最大力矩值，N·m。

3.2 模糊PID修正算法

力矩分配策略依赖于对车辆阻力的估计，然而在实际控制过程中阻力的估计值与实际值之间不可避免地会存在一定的偏差，为了消除外部参数变化对控制效果的影响，提高控制系统鲁棒性，在稳态转向过程中内外侧履带作用力分配的基础上引入PID算法进行纵向车速控制。PID算法的输入是根据驾驶员的加速踏板变化量确定的速度变化率目标值与实际加速度反馈值之差。

考虑到在履带车辆由直驶进入转向的动态过程中模糊调节力矩与PID调节力矩同时存在，为了避免PID调节力矩为负值时对模糊控制产生影响，引入模糊因子（1-x）N来实现模糊控制与PID控制的算法融合，它可在瞬态过程中模糊控制发挥作用时通过模糊因子来弱化PID的作用，而当转向即将进入稳态时模糊控制效果消失，同时将控制权重交还给PID算法以实现更为稳定的控制效果。

在模糊控制算法与PID调节的共同作用下，外侧电机目标力矩为

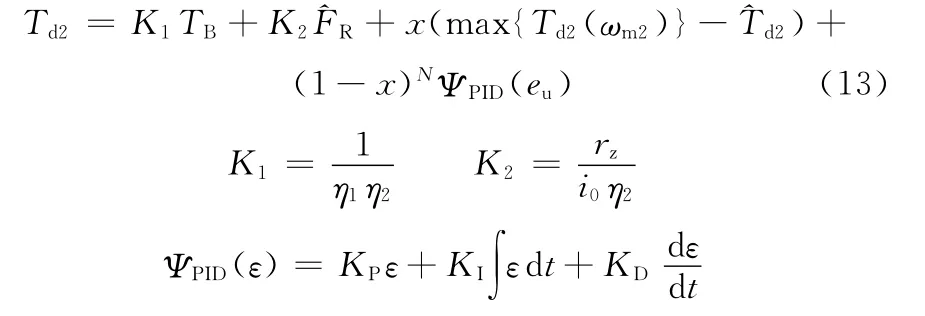
式中，KP、KI、KD为 PID参数，通过仿真进行整定；η1、η2分别为右侧和左侧电机输出轴到主动轮的传动效率；i0为主减速器传动比；ε为PID算法的输入量；N为模糊算法对PID的弱化系数，N越大，则模糊输出因子对PID算法的抑制越强。

另外对内侧电机制动力矩施加同样的模糊调节力矩：

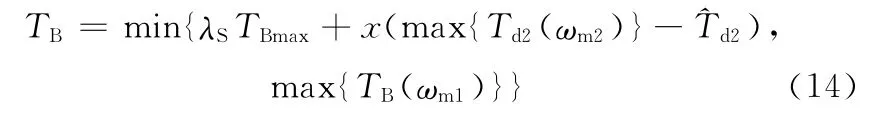
这样的优点在于可以进一步提高转向动态响应能力，同时还可以削弱在瞬态过程中由于PID算法的控制效果被弱化而导致的速度波动。

4 MATLAB仿真及结果

在MATLAB／Simulink环境下建立双侧电传动履带车辆转向仿真模型对上述模糊PID转向控制策略进行仿真验证，控制模块的仿真模型如图6所示，仿真时在第10s给出转向盘角阶跃输入。

模糊控制与PID算法的调节力矩如图7所示，图8为转向半径的仿真结果。可以看出，从第10s履带车辆进行转向开始，有模糊控制的力矩分配策略在10.8s时即达到了稳态，其动态响应过程约为0.8s，而直接力矩分配策略则需要1.5s。可见所提出的模糊控制算法明显改善了转向的动态响应能力，使动态响应时间缩短了大约0.7s，同时还能实现正确的稳态转向半径。

为了对PID算法的调节效果进行验证，对地面阻力系数加一扰动量（图9），来模拟在控制参数估计值与实际值存在偏差时的控制效果。驱动力、地面阻力与纵向车速的仿真结果如图10、图11所示。

显然，与直接转矩控制策略相比，在引入模糊PID算法之后，有效地消除参数摄动对车辆运行状态的影响，车速基本达到稳定。

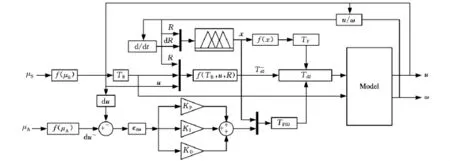
图6 模糊PID转向控制算法仿真模块

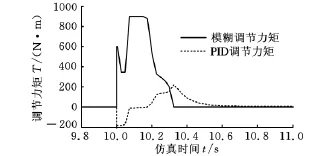
图7 模糊与PID调节力矩

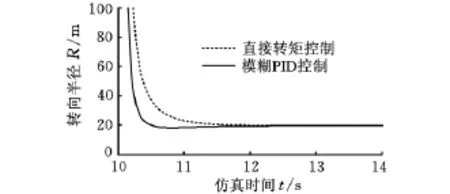
图8 转向半径仿真结果

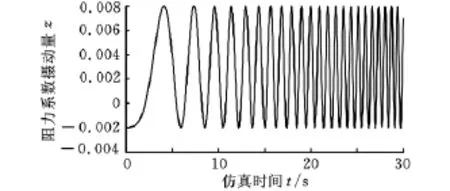
图9 地面阻力系数波动量

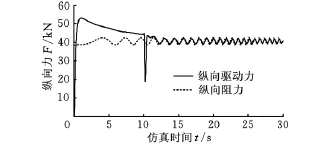
图10 驱动力与地面阻力仿真结果

模糊控制与PID算法的调节力矩如图12所示。从仿真结果可以看出，与未加参数摄动量时相似，在转向瞬态过程模糊控制发挥了较大作用，PID算法的调节作用被弱化，当转向进入稳态之后随着模糊控制的退出PID算法逐渐开始发挥作用。

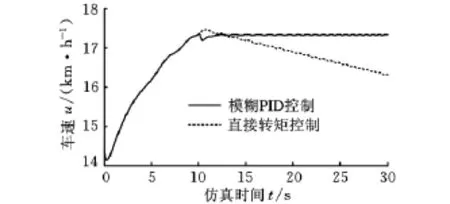
图11 车速仿真结果

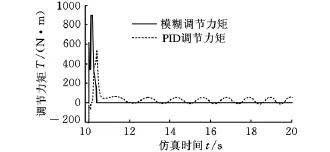
图12 模糊与PID调节力矩

5 结论

（1）假设外部阻力一定的情况下，当履带车辆的转向进入稳态阶段之后，其转向半径只与内侧履带制动力有关。

（2）缩短从直驶进入转向稳态阶段之间的动态响应时间是提高履带车辆转向轨迹可控性的主要措施。在转向瞬态过程中暂时增大外侧履带驱动力可以有效缩短动态响应时间。

（3）仿真结果表明所提出的控制策略可以实现良好的履带车辆转向性能，转向轨迹稳定可控且提高了转向动态响应能力，与直接转矩控制相比可缩短动态响应时间约0.7s。

［1］孙逢春，陈树勇，郭汾.基于转矩控制策略的电传动履带车辆驱动特性研究［J］.兵工学报，2007，28（2）：129-133.Sun Fengchun，Chen Shuyong，Guo Fen.Research on Driving Performances of Electric Transmission Tracked Vehicles Based on Torque Control Strategy［J］.Acta Armamentari，2007，28（2）：129-133.

［2］Rahman A，Yahya A，Zohadie M，et al.Simulated Steerability of a Segmented Rubber Tracked Vehicle during Turning on Sepang Peat Terrain in Malaysia［J］.International Journal of Heavy Vehicle Systems 2005，12（2）：139-168.

［3］Chen Zeyu，Zhang Chengning.Control Strategy Based on BP Neutral Network Plus PID Algorithm for Dual Electric Tracked Vehicle Steering［C］／／2nd International Conference on Advanced Computer Control.Shenyang，2010：584-587.

［4］Park Dong，Lim Sung-Kyun，Kwak Yoon Keun.Design and Optimisation of Variable Geometry Single-tracked Vehicle for Climbing Stairs［J］.International Journal of Vehicle Design，2007，43（1／4）：221-236.

［5］Wang G G，Wang S H，Chen C W.Design of Turning Control of Tracked Vehicle［J］.IEEE Control System Magazine，1990，17（2）：122-125.

［6］陈泽宇，张承宁，李军求，等.双侧电传动履带车辆小半径转向控制策略［J］.中国机械工程，2010，7（13）：1632-1637.Chen Zeyu，Zhang Chengning，Li Junqiu，et al.Dual Electric Tracked Vehicle Small-radius Turning Control Strategy［J］.China Mechanical Engineering，2010，7（13）：1632-1637.