3－PRPS并联机构的位置正解及应用研究

郭宗和 朱松松 崔荣江 杨启志

1.山东理工大学，淄博，255049 2.山东省农业机械科学研究所，济南，250100

3.江苏大学，镇江，212013

0 引言

并联机构因其刚度大、积累误差小、承载能力大、动力性能好等优点而得到广泛应用［1］。1988年 Behi［2］首先提出了 3－PRPS 并联机构，Shim等［3］分析了3－PRPS并联机构的运动学反解、工作空间，Chuang等［4-5］对该机构进行了动力学分析及控制规划，拓展了该机构运动学特性研究的思路，另外，王建平等［6］初步探讨了该机构的位置正解，并通过仿真分析研究了机构参数q对机构运动性能的影响。但有关该并联机构的位置正解还无详细的研究报道。位置正解一直是一个挑战性的问题并且受到极大的关注。

目前并联机构的正解求解方法主要有数值法和封闭解法［7］。第一个被研究位置正解解析解形式的并联机构是 6－3型 Stewart并联机构。Innocenti等［8］用封闭解法分析了 6－3 型Stewart并联机构的位置正解。贺利乐等［9］用改进的遗传算法对一种混合驱动并联机构的位置正解进行了研究。

本文根据3－PRPS并联机构自身的结构特点，通过建立约束方程，分析该并联机构位置正解的封闭解形式，并且采用向量之间的内积与外积分析了机构的位置反解，研究了该机构在车船用减振平台方面的应用。

1 3－PRPS并联机构的结构

3－PRPS并联机构如图1所示，该并联机构由3个水平滑块P1、P2、P3，3个竖直作用连杆L1、L2、L3，动平台 B1B2B3，定平台 A1A2A3等组成，其中动平台和定平台均为正三角形，且动平台外接圆半径为r，定平台内切圆半径为R，通过改变滑块的位移和竖直连杆的长度改变动平台在空间的位姿。根据3－PRPS并联机构的特点，在定平台的重心位置O上建立定坐标系OXYZ，在动平台的重心位置o上建立动坐标系oxyz。

图1 3-PRPS并联机构简图

2 3－PRPS并联机构位置正解

对于3－PRPS并联机构的位置正解，就是已知水平滑块的位移Si(i=1，2，3)和竖直连杆的杆长 Li，求解动平台的位姿(XP，YP，ZP，α，β，γ)，为了方便正反解数值验证，现将位姿转化为Bi点在定坐标系中的坐标。Bi点坐标确定，动平台的位姿则确定。

定义θi为竖直连杆与定平台之间的夹角，则由Pi点坐标即可推导出 Bi点在定坐标系下的坐标:

得出关于 θ1、θ2、θ3的 3 个方程:

式中，A、B、D、E、F为机构的已知几何参数及输入变量的函数。

令u=tanθ1/2，v=tanθ2/2，w=tanθ3/2，利用半角公式:

将式(1)～式(3)进一步简化为

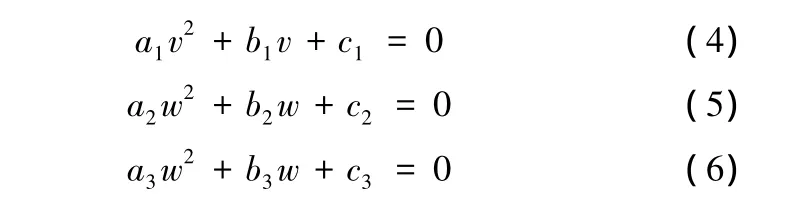
利用Sylvester消元法，从式(5)和式(6)中消去w，得到关于u和v的4次方多项式，将该多项式写成v的显式为

其中，各系数kj(j=1，2，…，5)仅是关于u的不高于4次的函数，用 v乘式(7)，用 v、v2、v3分别乘式(4)共得4个附加方程，连同式(4)、式(7)共6个方程，写成矩阵形式:

由于［v5v4v3v2v 1］T≠0，所以这个齐次方程组有非零解的充分必要条件是其系数行列式等于零，即

式(9)是关于u的16次代数方程，由此可解得u的值，联立式(4)和式(7)，可解得v，最后联立式(5)和式(6)可得到w。

u、v、w 求得后即可确定 θi，从而求得 B1、B2、B3点在定坐标系下的坐标，最终确定动平台的位姿。

3 3－PRPS并联机构位置反解

位置反解可以简单描述为:已知动平台的位姿(XP，YP，ZP，α，β，γ)，求解水平滑块的位移 Si和竖直连杆的杆长Li，Si为正表示滑块沿逆时针方向移动，反之沿顺时针方向移动。

本文选择(XYZ)RPY角坐标表示法描述姿态旋转矩阵，即首先将动坐标系绕定坐标系的X轴旋转γ角，再绕定坐标系的Y轴旋转β角，最后绕定坐标系的Z轴旋转α角，则两坐标系之间的变换矩阵为

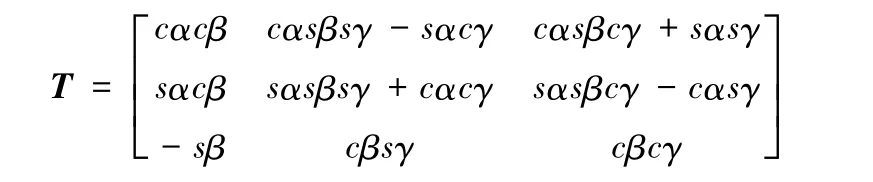
其中，cα =cosa，sα =sinα，其他类推。为了方便运算，用以下变量来表示矩阵中的元素，即

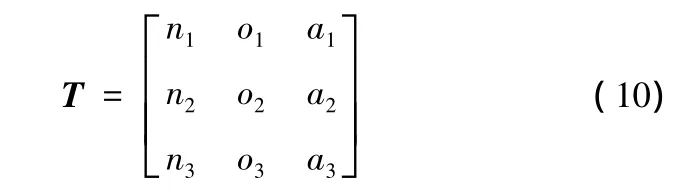
则有

式中，Bi为B点在定坐标系中的坐标;bi为B点在动坐标系中的坐标;P为o点在定坐标系中的坐标。

在 △A1B1A2中，P1B1垂直 A1A2，所以

同理可得:

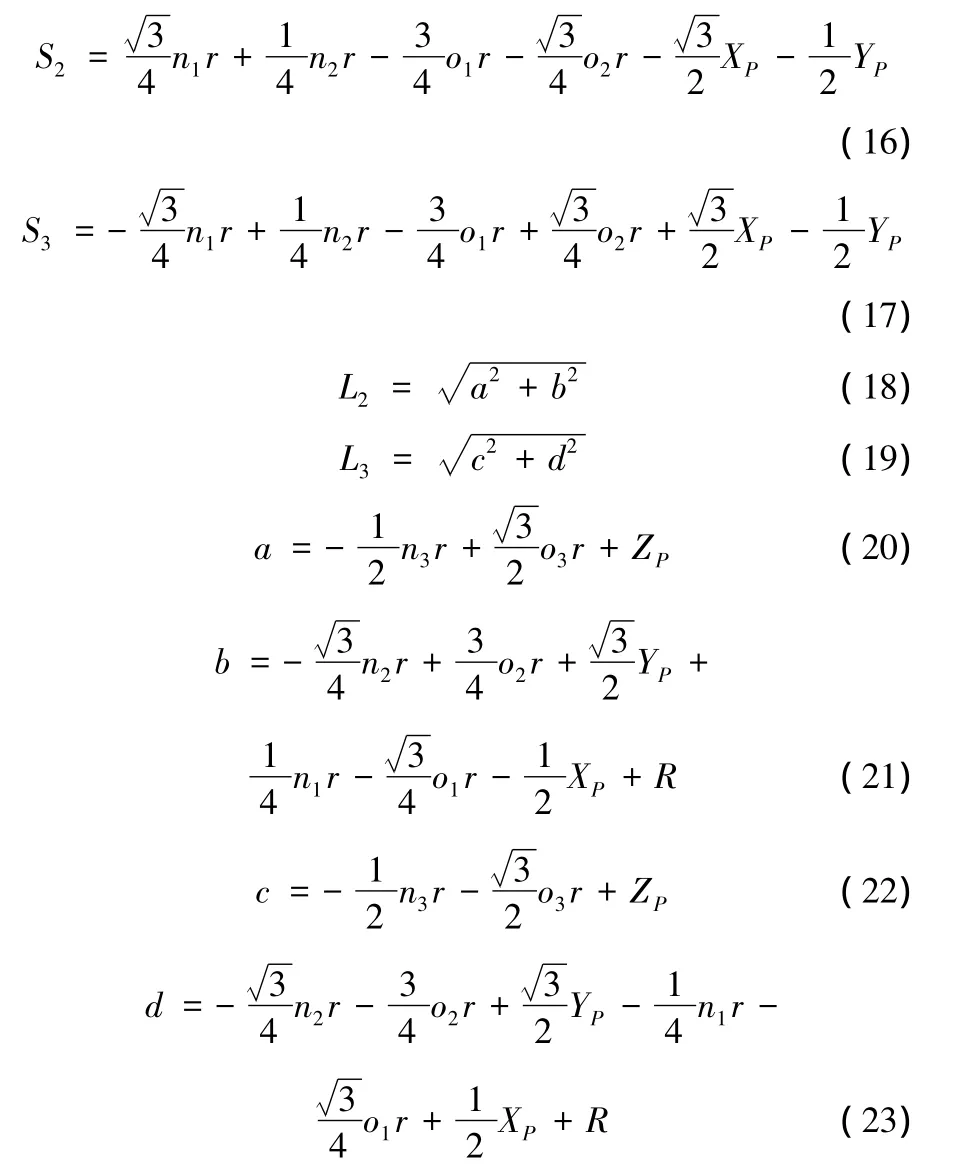
动平台的位姿已知时，则由以上公式可以求出3个杆长Li和3个滑块的位移Si，即求得机构的位置反解。

4 数值验证

选取机构参数如下:r=10mm，R=13mm，动平台初始位姿(0，0，4mm，0，0，0)，取(S1=0，S2=0，S3=0，L1=5mm，L2=5mm，L3=5mm)作为正解的输入。

运用MATLAB软件编程求解，由前面正解分析可知，封闭解为一元16次方程，编程求解将会有16个解，这里由于u、v、w值不可能为复数，故舍去所有的复数解，对于上述的正解输入，产生了8组实数解和8组复数解，只保留8组实数解。由8组实数解可进一步求得Bi点在定坐标系下的坐标，求解结果如表1～表3所示。

表1 8组实数解对应B1点坐标 mm

表2 8组实数解对应B2点坐标 mm

表3 8组实数解对应B3点坐标 mm

根据表1～表3画出8组实数解对应的上平台位姿，如图2所示。

由图2可以看出，8组位姿是呈对称分布的，其中，图2h正是我们所给出的机构的初始位姿，从而验证了正解求解的正确性，另外，其他图中所示的动平台位姿均受到了干涉的影响，实际应用中是不可能达到的。

取上述所得的8组实数解作为并联机构位置解的输入，求解机构位置反解，并将求解结果与正解的输入进行对比，求解结果如表4所示。

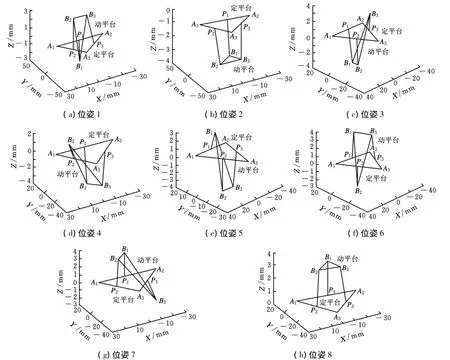
图2 8组解对应的动平台位姿

表4 8组实数解对应位置反解 mm

5 应用

由上述正解分析可知，在保证水平滑块位移及竖直连杆杆长均为初始位姿的情况下，机构理论上只能有8个位姿，如图2所示，但由于受干涉的影响，机构实际上只能实现一种位姿，即图2h。

这种正解唯一性的特性可以很好地应用在减振平台上，即动平台在受到来自各个方向的振动时，能通过水平滑块及竖直连杆移动副处的阻尼作用，最终保证动平台回到初始位置，而不会因为位置正解的多解性偏离初始位置，减振平台模型如图3所示。

图3 多维减振平台实体模型

为了研究减振效果，在水平滑块移动副处添加刚度k=4.0N/mm、阻尼c=1.0N·s/mm的阻尼弹簧，在竖直连杆移动副处添加k=4.0N/mm、c=10N·s/mm的阻尼弹簧，并且对动平台中心施加3个脉冲力 F和脉冲力矩 M，力的幅值为100N，力矩的幅值为100N·mm，脉冲总时间为0.4s，脉冲函数为:STEP(time，0，0，0.1，100)+STEP(time，0.1，100，0.3，－100)+STEP(time，0.3，－100，0.4，0)，进行 End time=10，steps=100的动力学仿真，可以得到在脉冲激励下，动平台的加速度随时间变化的曲线，如图4所示，由曲线可以看出在同时受到脉冲力和脉冲力矩时，动平台的加速度有明显的衰减，因此该机构可以达到很好的减振效果。

图4 动平台位移加速度曲线

6 结论

(1)对3－PRPS并联机构进行了位置正解分析，通过建立约束方程，将含6个未知数6个方程的方程组简化为含3个未知数3个方程的方程组，减小了计算量，提高了求解速度。

(2)基于3－PRPS并联机构自身的结构特点，通过运用向量之间的内积与外积，求解了机构的位置反解，该方法简单快速，避免了大量复杂的运算。

(3)利用数值方法对机构的位置正反解进行了验证，得出了正解的计算结果与反解的计算结果相吻合的结论，验证了正反解求解的正确性。

(4)研究了该机构在车船用并联机构减振平台方面的应用，运动学仿真结果表明该机构具有良好的减振性能。对位置解的分析与研究，为该机构在车船用并联机构减振平台方面的应用奠定了坚实的理论基础。

［1］Li Yangmin，Xu Qingsong.Design，Analysis and Applications of a Class of New 3－DOF Translational Parallel Manipulators［M］.Vienna:In.Tech.Education and Publishing，2008.

［2］Behi F.Kinematics Analysis for a Six Degree of Freedom 3－PRPS Parallel Mechanism［J］.IEEE Journal of Robotics and Automation，1988，4(5):561-565.

［3］Shim J H，Kwon D S.Kinematics Analysis and Design of a Six D.O.F.3－PRPS In－parallel Manipulator［J］.Robotica，1999，17:269-281.

［4］Chuang H，Chang Y.Singularity and Workspace A-nalysis of 3－PRPS Platform Control［J］.Journal of the Chinese Society of Mechanical Engineers，2000，21(6):555-565.

［5］Chuang H，Chang Y.Fuzzy Logic Weighting Crosscoupled Control for 3－PRPS Platform［J］.Journal of the Chinese Society of Mechanical Engineers，2001，22(1):61-69.

［6］王建平，彭凯.基于ADAMS的一种新型六自由度并联机构的参数分析与仿真［J］.机械传动，2011，35(5):31-35.Wang Jianping，Peng Kai.Parameter Analysis and Simulation of a New Six－DOF Parallel Manipulator Based on ADAMS［J］.Journal of Mechanical Transmission，2011，35(5):31-35.

［7］Dasgupta B，Mruthyunjaya T S.The Stewart Platform Manipulator:a Review［J］.Mechanism and Machine Theory，2000，35:15-40.

［8］Innocenti C，Castelli V P.Direct Position Analysis of the Stewart Platform Mechanism［J］.Mechanism and Machine Theory，1990，25(6):611-621.

［9］贺利乐，刘宏昭.一种六自由度混合驱动并联机构的位置正解分析研究［J］.中国机械工程，2007，18(8):920-923.He Lile，Liu Hongzhao.Research on Forward Solution of Position of 6－DOF Hybrid Driven Parallel Mechanism［J］.China Mechanical Engineering，2007，18(8):920-923.