数控成形砂轮磨齿机床几何误差分析与函数补偿法

杨清艳 韩 江 张魁榜 夏 链

合肥工业大学，合肥，230009

0 引言

磨齿加工是高性能齿轮制造最主要的手段和工艺方法，其主要特点是可以全面纠正齿轮磨削前的各种误差，最终获得高的加工精度。在目前科学技术支撑条件下，成形磨齿机可能是目前制造水平下获得最高精度的高生产率齿轮加工机床，必将成为未来高端磨齿机产品的主流［1］，而其精度指标是影响工件加工精度的重要因素。提高机床精度和减小加工误差的主要途径一方面是提高机床的机械性能，另一方面是实时地对机床空间误差进行补偿［2-3］。本文主要针对QCYK7332A数控成形砂轮磨齿机，利用多体系统理论以及 4×4Denavit－Hartenberg齐次变换矩阵［4-7］，分析了机床几何误差的来源，建立了误差模型，提出通过函数法来对误差进行预测进而实时地在线补偿误差。

1 基于多体系统理论的成形磨齿机空间误差模型及误差分析

1.1 成形磨齿机结构及拓扑结构描述

QCYK7332A数控成形磨齿机是直径320mm以下的高精度、大批量生产以及特种齿轮磨削的磨齿设备。磨齿过程中若不考虑砂轮的修整，则由机床的2根移动轴 X、Z和3根旋转轴A、B、C完成加工。图1为数控成形磨齿机床及其结构示意图。

图1 数控成形磨齿机床及其结构示意图

床身基座1作为B1体，将磨床系统分为两个分支:①分支一为床身基座1、砂轮架进刀X轴2、砂轮架走刀轴Z轴3、刀架旋转轴A轴4、B旋转轴5;②分支二为床身基座1、工件轴(C旋转轴)6。

对于分支一，以床身基座B1体为起点，沿远离B1的方向，以自然数增长顺序依次标定每个部件的序号:床身基座B1，砂轮架进刀X轴B2，砂轮架走刀轴Z轴B3，刀架旋转轴A轴B4，B旋转轴B5，工件轴(C 旋转轴)B6。

根据以上数控成形磨齿机的拓扑结构描述，得到表1和图2所示的成形磨齿机的低序列体阵列及其拓扑结构示意图。

表1 成形磨齿机低序列体阵列

图2 拓扑结构示意图

1.2 数控成形磨齿机系统相邻体间变换矩阵的建立

对于数控成形磨齿机QCYK7332A，其加工过程由2根移动轴X、Z，3根旋转轴A、B、C完成。根据机床多体系统理论，它在加工中总共包括32项空间误差:线性位移误差Dx(X)、Dz(Z);垂直直线度误差 Dy(X)、Dx(Z);水平直线度误差Dz(X)、Dy(Z);滚转误差 Ax(X)、Az(Z);俯仰角度误差Ay(X)、Ax(Z);偏摆角度误差Az(X)、Ay(Z);垂直度误差 SYX、SZY;安装误差 Dz(C)、Dx(A)、Dy(B);垂直直线度误差 Dx(C)、Dy(A)、Dz(B);水平直线度误差Dy(C)、Dz(A)、Dx(B);俯仰角误差 Ax(C)、Ay(A)、Az(B);偏摆角误差 Ay(C)、Az(A)、Ax(B);转角误差 Ac(C)、Aa(A)、Ab(B)。

其中，D表示直线位移误差、A表示旋转误差，S表示垂直误差，下标表示位移方向、括号内字母表示误差轴。

1.2.1理想状态下各运动副的坐标齐次变换矩阵

(1)移动副坐标齐次变换矩阵。当机床的砂轮架进刀X轴B2、砂轮架走刀轴Z轴B3移动无误差时，其相邻体之间的齐次变换矩阵为

(2)转动副坐标齐次变换矩阵。同理，当A、B、C轴无旋转误差时，其相邻体之间的变换矩阵为

式中，φ为A轴绕其x轴的转角;α为C轴绕其z轴的转角;β为B轴绕其y轴的转角。

1.2.2考虑误差的成形磨床各运动副坐标齐次变换矩阵

在机床的加工过程中，如果各种误差为零，则砂轮边缘上点的空间坐标系t与工件的空间坐标系p是重合的;但实际中，由于各种误差存在，砂轮边缘上点的空间坐标与工件的空间坐标将发生分离，此时砂轮边缘上点与工件之间的坐标变换矩阵就是所求的误差模型矩阵。

1.2.2.1 移动副坐标齐次变换矩阵

当砂轮架进刀X轴体B2存在沿x轴轴向的线性位移误差Dx(X)，在XY平面，存在沿y、z轴的直线度误差Dy(X)、Dz(X)，绕 y、z轴的偏摆角误差Ay(X)、Az(X)，绕x轴滚转误差Ax(X)时，可得相邻体之间的坐标变换矩阵为

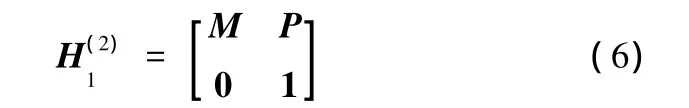
式中，P为平移变换矩阵;M为旋转变换矩阵。

其中，x为描述机床导轨沿 X轴的设定运动量，x=［x10 0］T;δx为机床导轨沿参考方向移 动 时 在 x、y、z 方 向 的 位 移 误 差，δx=［Dx(X)Dy(X)Dz(X)］T;θx为移动轴与参考轴 平 面 YX、ZX 的 垂 直 度 误 差，θx=［0 SYXSZX］T。因此可将式(6)扩展为

同理可得砂轮架走刀轴Z轴体B3沿z轴运动时，相对于体B2的坐标变换矩阵:

1.2.2.2 转动副坐标齐次变换矩阵

当砂轮B轴体B5存在绕y轴的角位移误差Ay(B)，沿 x轴、y轴、z轴的直线度误差 Dx(B)、Dy(B)、Dz(B)，沿 x轴、z轴的偏摆角误差 Ax(B)、Ay(B)、Az(B)时，可得砂轮B轴体B5相对于相邻体B4包含误差的变换矩阵为

式中，R为旋转变换矩阵;Q为平移变换矩阵。

可得砂轮B轴体B5相对于相邻体B4包含误差的变换矩阵为

同理，也可得工件C轴体B6相对于相邻体B1，以及刀架旋转轴A轴体B4相对于相邻体B3包含误差的变换矩阵分别为

1.3 磨床误差模型的建立

(1)在理想(无误差)情况下，砂轮边缘上点坐标系t和工件坐标系p在空间重合，因此砂轮边缘上点坐标系t相对于机床底座体B1基坐标系的齐次坐标变换等于坐标系p相对于机床底座体B1基坐标系的齐次坐标变换，即

根据多体系统理论并结合图1所示磨床的结构，可以分别得到

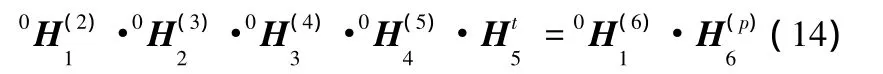
可以得出工件主轴坐标系c相对于工件坐标系p的齐次变换矩阵:

(2)在有误差的情况下，t与p在空间上产生了分离，t相对p的齐次变换矩阵即为误差矩阵，也就是所求的误差模型:

将式(15)代入式(16)，运用软件进行计算，可得到所要求的误差模型。基于小误差假设的综合误差矩阵为

将式(16)展开并舍去二次及二次以上的分量，再结合式(18)得到该磨床的2个位置及3个转角的综合误差模型如下:

其中

1.4 砂轮边缘上点与齿轮几何误差规律分析

根据以上模型，式(19)～式(24)表示了各运动轴运动过程中的误差与砂轮边缘上点的误差之间的函数关系。由于各轴之间存在运动关系，最终将各几何误差转化到了砂轮上，引起砂轮在运动中偏移理想的位置，从而导致加工出来的齿轮产生齿形误差。以刀具轴B轴旋转副的误差为例，说明各运动轴加工过程中的误差，进而将误差转移到了砂轮边缘上，引起砂轮偏离原来的位置。图3为只考虑B轴所引起的误差并设其他运动轴所引起的误差为零时，得到的砂轮尖上误差与B轴偏角误差关系图。图3a所示为只考虑B轴绕其坐标系y轴旋转的误差以及B轴绕x轴的角度误差时，砂轮尖绕zT(下标T表示砂轮)轴的角度误差;图3b所示为只考虑B轴绕x轴的角度误差以及B轴绕z轴的角度误差时，砂轮绕xT轴的角度误差;图3c所示为只考虑B轴旋转副的误差时，砂轮尖绕yT轴的角度误差。对比表明，B轴转动误差对砂轮尖绕zT轴转动误差的影响较大，而对绕xT轴转动误差的影响较小。也说明了B轴绕其x、y、z轴的角度误差以及旋转时所引起的角度误差转化到了砂轮尖，引起了砂轮尖绕其xT、yT、zT轴的角度误差。由加工原理可知，若在这种情况下加工齿轮，则会造成工件的齿形误差、齿向误差、压力角误差等。

图3 砂轮尖误差与X轴误差关系图

2 几何误差补偿

图3及式(19)～式(24)更加清晰地说明了各轴误差会导致砂轮尖误差，进而在加工过程中转移到工件上，出现齿形误差、齿向误差、接触线误差、压力角误差等，而磨齿加工是齿轮加工的精加工，为了达到预期加工工件的精度，减小工件的误差，应采取恰当的误差补偿方法进行补偿。目前误差补偿有两种方法——硬件补偿法和软件补偿法，考虑到数控硬件误差补偿需要在机床上外加控制器及硬件电路，成本较高且设计开发周期较长、通用性较差［8］，因此本文选用软件补偿。

2.1 基于函数法的软件误差补偿

软件误差补偿［9］主要研究数控机床误差的影响因素以及计算机软件误差补偿技术，从而提高数控机床的加工精度和效率。软件误差补偿的特点是不需改变加工设备或采用硬件电路等辅助设备即可提高数控机床的加工精度。本文基于多体系统运动学理论建立机床几何误差模型，采用函数法来进行误差补偿，即用误差补偿程序完成补偿任务。我们开发了具有误差在线分析和补偿功能的可内嵌于数控系统内部的补偿模块，该模块利用“反馈截取”方式获取信号，在模块内部独立完成信号的处理和综合，实现在线的动态误差预测和补偿量计算，为齿轮机床数控系统提供修正后的控制量输出。该函数法误差预测与补偿模块已用于自主研发的ARM+DSP+FPGA国产齿轮数控系统上，其原理如图4所示。其主要的软件程序包括:①各误差轴的误差表达式的数控程序;②砂轮尖误差表达式程序;③误差补偿程序。

图4 误差补偿流程图

在上层的ARM模块中编写以上所需要的各种误差程序;在加工过程中，通过底层的DSP控制各轴的运动，并把各轴位置运动量反馈给ARM;由各误差轴的误差表达式的数控程序采集各轴的信息，并运算出各轴的偏差量以及预测出下一步的误差量;将各轴的偏差量传递给砂轮尖误差表达式程序，进而计算出砂轮尖偏离理想位置的量;最后由误差补偿程序输出砂轮的最终补偿后的位置坐标值。

2.2 实例

2.2.1 Renishaw激光干涉测量误差

针对QCYK7332A数控成形磨齿机存在的误差值，本文仅以测量X轴的角度误差为例说明几何误差测量数据处理以及误差预测与补偿的过程。实验中所采用的测量仪器是Renishaw ML10激光干涉仪。运用Renishaw软件和控制仪器对每个方向进行3次测量，一旦安装位置确定好后，每一次测量都使用同样的测量过程。使用软件记录每次增量为10mm的总长度为100mm的11个定点测量值。仪器的参数设定之后，可以使用手动控制轮让机器对照软件相同的增量而运行，其测量时装置的安装如图5所示。

图5 测量时Renishaw激光干涉仪安装位置

2.2.2角度误差(俯仰角误差、偏摆误差)

角度误差包括俯仰角误差和偏摆角误差，系统会测量出到目标轴的横向和纵向位置之间的偏转角作为误差的大小。由于不能直接测量角度误差，故通过间接测量目标轴的横向和纵向位置，求其余弦值为俯仰角和偏摆角余弦。图6a所示为所测量的俯仰角余弦误差值，纵坐标表示当前位置相对于目标位置垂直差的余弦值，也就是要求的俯仰角及偏摆角余弦，可看出，三组数据有相同的变化趋势;图6b为偏摆余弦误差图，可看出，三次测量结果的误差值走势一致，也说明了测量的正确性。另外，当砂轮远离原点时，误差变大，成为累计误差。通过坐标值拟合最终得出其误差曲线的表达式如表2所示。

图6 误差曲线图(3次测量结果)

表2 误差多项式拟合

最终得出的角度误差余弦曲线表达式为

类似地，按照以上方法测量出其他轴的直线度误差、线性误差等并进行数据拟合，得出类似于式(25)与式(26)的误差曲线函数表达式，将其存入到系统中，以便于砂轮边缘点误差表达式程序调用;同时根据式(19)～式(24)编写砂轮尖误差关于各轴误差的补偿程序，计算出砂轮尖含移动副和转动副误差的小误差矩阵并进行相应的误差补偿，即:当机床各轴运动时，数控系统根据各轴的误差函数程序自动计算出各轴的误差值;砂轮尖误差表达式程序调用这一数值，计算出砂轮尖偏离理想点的误差值;误差补偿程序根据这一误差值反向进行补偿;最终修改砂轮移动量，使其更加确切地接近理想点，从而减小齿面误差。若误差点坐标比理论点大则下一点进给时理论点减去误差值，若误差点比理论点小则与此相反。

3 结论

通过对数控成形砂轮磨齿机床加工过程的分析，建立了机床空间几何误差模型，用软件仿真出B轴运动误差所引起砂轮尖角度误差的变化趋势，提出了对机床几何误差进行预测和实时补偿的函数补偿方法。以Renishaw激光干涉仪测量机床的角度为例，说明了实验数据的处理以及如何进行误差预测与补偿。当机床尺寸改变但机床结构不改变时，只需要改变各轴误差拟合曲线的程序就可以进行几何误差预测与补偿，因而该方法通用性强，从而为提高齿轮成形磨削加工精度提供了理论依据。

［1］张四弟，左键民，张兆祥，等.磨齿技术与装备及其发展趋势［J］.制造技术与机床，2011(2):46-48.Zhang Sidi，Zuo Jianmin，Zhang Zhaoxiang，et al .Deveoping Trend of Gear Grinding Technologies and Equiment［J］.Manufacturing Technology ＆ Machine Tool，2011(2):46-48.

［2］杨建国.数控机床误差综合补偿技术及应用［D］.上海:上海交通大学，1998.

［3］Okafor A C，Ertekin Y M.Derivation of Machinetools Error Models and Error Compensation Procedure for Three Axes Vertical Machining CenterUsing Rigid Body Kinematics［J］.International Journal of Machine Tools and Manufacture，2000，40(10):1199-1213.

［4］任永强，杨建国，窦小龙，等.五轴数控机床综合误差建模分析［J］.上海交通大学学报，2003，37(1):70-75.Ren Yongqiang，Yang Jianguo，Dou Xiaolong，et al.Analysis on the Error Synthesis Model of a Five－axis Machine Center［J］.Journal of Shanghai Jiaotong University，2003，37(1):70-75.

［5］Wang Shuxin，Yun Jintian，Zhang Zhifei，et al.Modeling and Compensation Technique for the Geometric Errors of Five－axis CNC Machine Tools［J］.Hinese Journal of Mechanical Engineering，2003，16(2):197-201.

［6］粟时平，李圣怡.王贵林.多轴数控机床的通用运动学综合空间误差模型［J］.国防科技大学学报，2001，23(4):45-49.Su Shiping，Li Shengyi，Wang Guilin.A Universal Synthetric Volumetric Error Model of Multi－axis NC Machine Tool Based on Kinematics［J］.Journal of National University of Defense Technology，2001，23(4):45-49.

［7］Jung J H，Choi J P.Machining Accuracy Enhancement by Compensating for Volumetric Errors of a Machine Tool and On－machine Measurement［J］.Journal of Materials Processing Technology，2006，174(1/2/3):56-66.

［8］龙云泽.五轴联动螺旋锥齿轮磨齿机各轴几何误差测量与补偿［D］.长沙:中南大学，2010.

［9］王一丁，张国雄.数控加工中心的位置误差补偿模型［J］.计量学报，1995，16(3):200-205.Wang Yiding，Zhang Guoxiong.The Position Error Compensation Model for CNC Machining Center［J］.Acta Metrologica Sinica，1995，16(3):200-205.