新型灰关联分析方法研究及其在数控机床主轴故障识别中的应用
2013-12-05杨东升李红卫孙一兰尹震宇
杨东升 李红卫,2 孙一兰 尹震宇
1.中国科学院沈阳计算技术研究所,沈阳,110171 2.中国科学院研究生院,北京,100039
0 引言
故障识别是一种利用设备当前状态信息和历史状况,采用一定分析方法对设备状态进行评价的状态识别技术。在设备运行过程中,故障与征兆之间没有确定的映射关系,因此可以将设备看作是一个复杂的灰色系统。
灰色系统理论作为一种处理非确定性问题的方法,由邓聚龙[1]于20世纪80年代提出,经过多年发展,该理论已应用于预测、线性规划、系统控制等领域[2-4]。灰关联分析方法作为灰色理论的一个重要组成部分,目前在故障识别领域被广泛应用[5-6],并取得了良好效果。但是,这种传统灰关联分析方法存在以下问题:①关联度值受分辨系数影响而不唯一;②关联度值离散性不强,结果趋于均化且可靠性低;③忽略了因子权重差异。
在传统灰关联分析方法的基础上,本文引入动态关联系数和因子权重系数,提出了新型灰关联分析方法,有效地解决了以上问题,将其运用于数控机床主轴故障识别中,提高了识别结果的可靠性和准确性,为数控机床及主轴生产厂家提供了良好的故障识别方法。
1 传统灰关联分析方法及其存在的问题
灰关联分析是事物间不确定关系的量化分析,灰关联度是一种数据到数据的“映射”,代表了不同研究对象之间的关联程度。
1.1 传统灰关联分析方法基础
设两组向量,一组为比较向量,记为Xi=(Xi(1),Xi(2),…,Xi(N))(i=1,2,…,m);一组为 参 考 向 量, 记 为 Yj=(Yj(1),Yj(2),…,Yj(N))(j=1,2,…,n)。Xi(k)和Yj(k)分别为Xi和Yj的第k个特征分量,其中k=1,2,…,N。传统灰关联分析过程如下:
(1)计算比较向量Xi与参考向量Yj在k点的关联系数ξij(k):
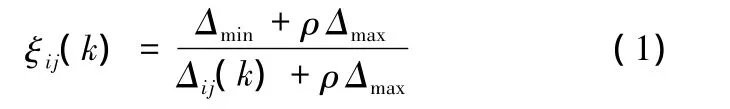
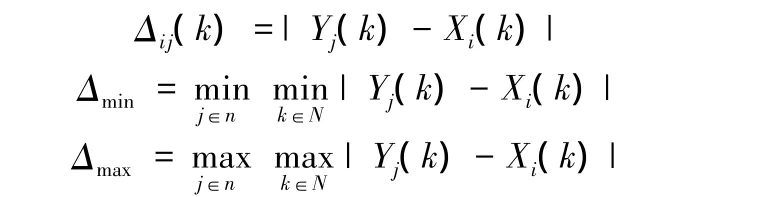
式中,ρ为分辨系数,传统灰关联分析中通常设为0.5。
(2)计算比较向量Xi与参考向量Yj的关联度γij:
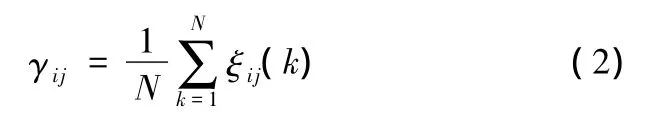
1.2 传统灰关联分析方法存在的问题
由式(1)、式(2)容易看出传统灰关联分析方法存在以下问题:
(1)关联系数ξij取值受分辨系数ρ不同取值的影响,导致关联度γij具有不唯一性。
(2)分辨系数ρ影响关联度分布区间,人为主观设置ρ=0.5将导致结果趋于均化,降低区分度。
(3)忽略不同因子权重差异,与工程实际应用不符。
2 新型灰关联分析方法
为解决1.2节中的问题,本文以传统灰关联分析方法为基础,在式(1)和式(2)中分别引入动态分辨系数和权重系数,形成新型灰关联分析方法。
2.1 动态分辨系数的确定[7]
定义1:比较向量Xi与所有参考向量Yj差值绝对值的均值为

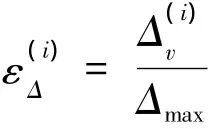

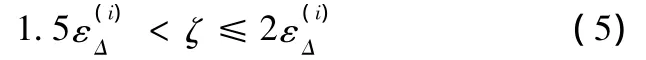
按上述方法动态选取ζ值,不仅使分辨系数取值具有一定的客观基础,而且有一定的智能性和灵活性。用动态分辨系数ζ替换式(1)中的静态分辨系数ρ,得到具有动态分辨系数的关联系数ξ'ij的计算公式:

2.2 加权系数的确定[8]
定义3:设序列 Yj(k)={Yj(1),Yj(2),…,Yj(k),…,Yj(N)}(j=1,2,…,n;k=1,2,…,N),各序列中各属性因子总和为
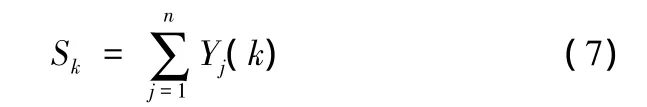
定义4:设一函数映射为f(x)=xe1-x+(1-x)ex- 1,称函数

为因子k的熵。


为因子k的相对权重。
定义6:若w为相对权重和,称函数

为因子k的权重。
式(2)取加权系数,结合式(6),即可得到新的关联度计算公式:

式(6)和式(11)即是本文提出的新型灰关联分析方法。与传统灰关联分析方法相比,该方法具有以下优点:
(1)不依赖于人为确定的分辨系数ρ,而是根据比较向量和参考向量动态计算分辨系数ζ,当比较向量和参考向量一定时,关联度值唯一。
(2)动态分辨系数ζ减少了人为主观因素对关联度分布区间的影响。
(3)赋予不同因子不同的权重,更能反映不同因子具有不同作用和地位的实际情况。
3 实例、结果及分析
3.1 诊断对象
本文所讨论的识别对象为数控机床主轴零件松动(F1)、配合松动(F2)和动不平衡(F3)三种状态。利用新型灰关联分析方法对其进行故障识别的原理如图1所示。
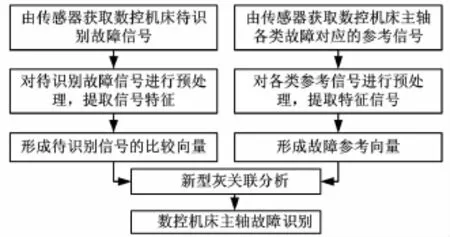
图1 新型灰关联分析故障识别原理图
本文分析的基础是文献[9]中有关数控机床主轴的振动信号,这些振动信号反映了数控机床主轴的三种状态,通过傅里叶变换进行频谱分析,可得到特定状态下的频谱特征。数控机床主轴故障机理分析及不同状态下的频谱图表明,不同状态对应不同的频谱特征,主要表现在频谱图中0.4~0.5倍频(f1)、1倍频(f2)、2 倍频(f3)、3倍频(f4)和大于3倍频(f5)的特征频段振幅不同。以F1状态振动信号为例,其频谱图如图2所示。因此,本文分析时将这5个特征频段振幅作为特征值。为更好地进行关联分析和故障识别,对特征值进行归一化处理,以得到识别需要的特征值:

其中,fk为每组原始数据中第k个特征值的取值,k=1,2,…,5。

图2 F1状态振动信号频谱图
为进行分析,针对每种状态,本文采用5组振动信号(每组包含100个数据),经傅里叶分析,得到特定状态下的5组特征值,归一化后,构成对应于三种状态的15组特征值(1~5对应于状态F1,6~10对应于状态 F2,11~15对应于状态F3),如表1所示。

表1 故障信号特征值表 cm
3.2 参考向量与比较向量的构造
选取表1中序号为1、6和11的行作为参考向量,形式为(Y1,Y2,Y3)T,其中Yj=(Yj(1),Yj(2),Yj(3),Yj(4),Yj(5))(j=1,2,3)。j=1 时,代表数控机床主轴处于F1状态;j=2时,代表数控机床主轴处于F2状态;j=3时,代表数控机床主轴处于F3状态。实际应用中,参考向量的选取影响识别结果的准确性和可靠性,可视特定故障状态下的所有特征值平均值为参考向量;另外,也可将所有特征值均作为参考向量,故障识别时,比较向量与每个参考向量进行新型灰关联分析,将得到的多个识别结果进行综合处理,可使识别结果更准确可靠。
选取表1中除序号为1、6和11之外的其他所有行作为比较向量,形式为(X1,X2,…,X12)T,其中 Xi=(Xi(1),Xi(2),Xi(3),Xi(4),Xi(5))(i=1,2,…,12),该组向量用来验证本文方法是否有效,其中,X1~X4为数控机床主轴F1特征信号;X5~X8为数控机床主轴F2特征信号;X9~X12为数控机床主轴F3特征信号。实际应用中,运行过程中获取的每一特征值均可作为比较向量。
3.3 故障识别及结果分析
3.3.1识别结果
根据2.1节和2.2节给出的方法,进行新型灰关联分析,得到参考向量各因子权重和状态识别结果,分别如表2和表3所示。表3中,ζ列表示特定比较向量对应的动态分辨系数;关联度列表示比较向量与各参考向量的关联强度,关联度值越大,表示关联程度越紧密。本文中,选取关联度值最大者为比较向量对应的故障状态。

表2 参考向量因子权重

表3 新型灰关联分析识别结果
从表3可得出以下结论:①新型灰关联分析方法可有效地识别数控机床主轴的三种状态;②比较向量所属故障状态对应的关联度值分量与其他分量的距离较大,识别结果可靠。
3.3.2对比分析
为进一步对新型灰关联分析方法进行讨论,本文将该方法识别结果与传统灰关联分析方法识别结果进行对比分析。另外,由于数控机床主轴故障特征参考向量难于获取,在少量参考向量情况下得到更为准确的识别结果在数控机床主轴故障识别中尤为重要,因此,本文还将该新型关联分析方法与神经网络识别结果进行对比分析。
(1)与传统灰关联分析方法的比较。传统灰关联分析方法计算过程所需数据与上述新型灰关联分析方法所使用的数据一致,根据1.1节介绍的传统灰关联分析计算方法,得到传统灰关联分析方法的识别结果,如表4所示。

表4 传统灰关联分析方法识别结果(ρ=0.5)
表4表明,传统灰关联分析方法也可有效地识别数控机床主轴的三种状态。关联度离散性表示关联度之间的安全隔离空间,关联度离散性越大,表示识别结果区分度越大,可靠性越高。现从关联度离散性方面对表3和表4进行分析,如图3所示。图3表明新型灰关联分析方法使关联度离散性增大,可有效避免因外界干扰或数据波动导致的识别错误,提高了识别结果的可靠性。

图3 关联度标准差对比图
(2)与神经网络的比较。将表1中序号为1、6和11的行作为BP神经网络的训练样本,其他行作为验证的比较向量。在总体学习误差分别为0.05、0.1和0.15时训练网络,得到在每种训练模式下的识别误差,求三种误差的平均值,并与新型灰关联分析方法识别误差进行对比,如图4所示。

图4 结果识别误差对比图
图4表明,在单样本情况下,相对于神经网络,新型灰关联分析方法可有效减小识别误差,提高识别结果的准确性,这说明新型灰关联分析方法比神经网络更适于经验样本数据少的故障识别场合。另外,在实验过程中发现,神经网络识别误差随总体学习误差的减小而减小,但总体学习误差的减小将导致训练步数增加,训练时间变长;此外,样本发生变化时,神经网络需重新进行训练,诊断效率降低。新型灰关联分析方法与其相比,计算量小,不需训练,过程简单,更适于有实时故障识别要求的场合。
4 结语
本文在分析传统灰关联分析方法及其存在问题的基础上,引入动态分辨系数和权重系数,提出了新型灰关联分析方法,减少了人为干预,提高了灰关联分析的可靠性和准确性。在此基础上,将该方法应用于数控机床主轴故障识别,取得了良好效果,同时给出了该方法识别结果与传统灰关联分析方法和神经网络识别结果的对比分析,证明了该方法的优越性。另外,这种新型灰关联分析方法属于广义的灰关联分析方法,可广泛应用于其他故障和信号识别领域,具有良好的实际应用价值。
[1]邓聚龙.灰色系统理论教程[M].武汉:华中理工大学出版社,1990.
[2]Wang M H.Grey-extension Method for Incipient Fault Forecasting of Oil-immersed Power Transformer[J].Electric Power Components and Systems,2004,32(10):959-975.
[3]赵磊,李原,余剑峰.支持变约束的装配顺序随需式规划方法[J].机械工程学报,2011,47(5):149-155.Zhao Lei,Li Yuan,Yu Jianfeng.Assembly Sequence Concomitant Planning Method Based for the Variation[J].Journal of Mechanical Engineering,2011,47(5):149-155.
[4]辛民,王西彬,解丽静,等.基于灰色理论的铣削参数优化方法研究[J].中国机械工程,2009,20(23):2807-2810.Xin Min,Wang Xibin,Xie Lijing,et al.Study on Milling Parameter Optimization Method Based on Gray Theory[J].China Mechanical Engineering,2009,20(23):2807-2810.
[5]刘军,卢炎生.一种粗集与灰色理论结合算法在柴油机故障诊断系统中的应用[J].小型微型计算机系统,2010,31(4):797-800.Liu Jun,Lu Yansheng.Application of One Combined Algorithm in Diesel Engine Fault Diagnosis System Based on Rough Set and Grey Theory[J].Journal of Chinese Computer System,2010,31(4):797-800.
[6]Jiang Lingping.Gas Path Fault Diagnosis System of Aero-engine Based on Grey Relationship Degree[J].Procedia Engineering,2011,15:4774-4779.
[7]东亚斌,段志善.灰色关联度分辨系数的一种新的确定方法[J].西安建筑科技大学学报(自然科学版),2008,40(4):589-592.Dong Yabin,Duan Zhishan.A New Determination Method for Identification Coefficient of Grey Relational Grade[J].Journal of Xi’an University of Arch.&Tech.(Natural Science Edition),2008,40(4):589-592.
[8]罗佑新,张龙挺,李敏.灰色系统理论及其在机械工程中的应用[M].长沙:国防科技大学出版社,2001.
[9]吴今培,肖健华.智能故障诊断与专家系统[M].北京:科学出版社,1997.
