一种基于快速傅立叶变换的平衡能力分析方法

【作 者】朱明，郑风，张琳琳，沈凌

上海医疗器械高等专科学校，上海市，200093

平衡能力是人体的一项重要生理机能，主要是指维持身体姿势，控制身体重心的能力，是一切静态与动态活动的基础能力。对于此能力的分析评估，可以为站立或行走时自身保持平衡进行初步的判断，从而为平衡功能缺失者提供准确地临床诊断，并采取有效的辅助治疗措施，最大程度的避免发生摔倒现象。本文主要介绍一种利用快速傅立叶变换对各种站立姿势下人体重心变化轨迹进行幅度-频率变换处理的平衡能力的评估方法。

1 快速傅立叶变换算法

快速傅立叶变换是数字信号处理领域一种很重要的算法，适用于任何起源产生的任何类型的波动。通过快速傅立叶变换的应用，可以及时将不同频段下不同站立姿势摆动的幅度变化显示出来。目前测试站立姿势主要包括：正常站立睁眼、正常站立闭眼、带直立脚垫睁眼、带直立脚垫闭眼、头前低30o闭眼、头后仰30o闭眼、头左偏闭眼和头右偏闭眼八种姿势，根据在一定频段范围内身体动摇的变化显示结果，判断人体平衡能力的大小。

1.1 4点基2时间抽取FFT算法

4点基2时间抽取FFT算法的流程见图1，具体计算，见式（1）。

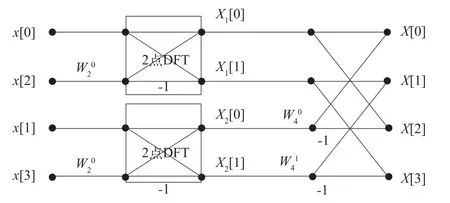
图1 4点基2时间抽取FFT算法流程Fig.1 Fourier transform algorithm of 4 point base 2 time extraction

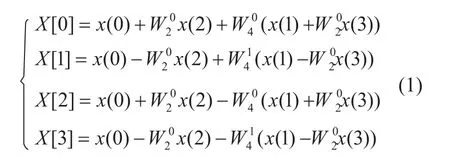
其中，x(0)、x(1)、x(2)、x(3)分别代表单位时间内采集到的重心距离原点的最大距离。X [0]、X [1]、 X [2]、 X [3]表示单位频率重心变化的最大幅值。WNm表示旋转因子，利用旋转因子的周期性、对称性进行合并、归类处理，可以减少运算次数。

1.2 8点基2时间抽取FFT算法

基于四点基2时间抽取FFT算法，本文主要采用的是8点基2时间抽取FFT算法。

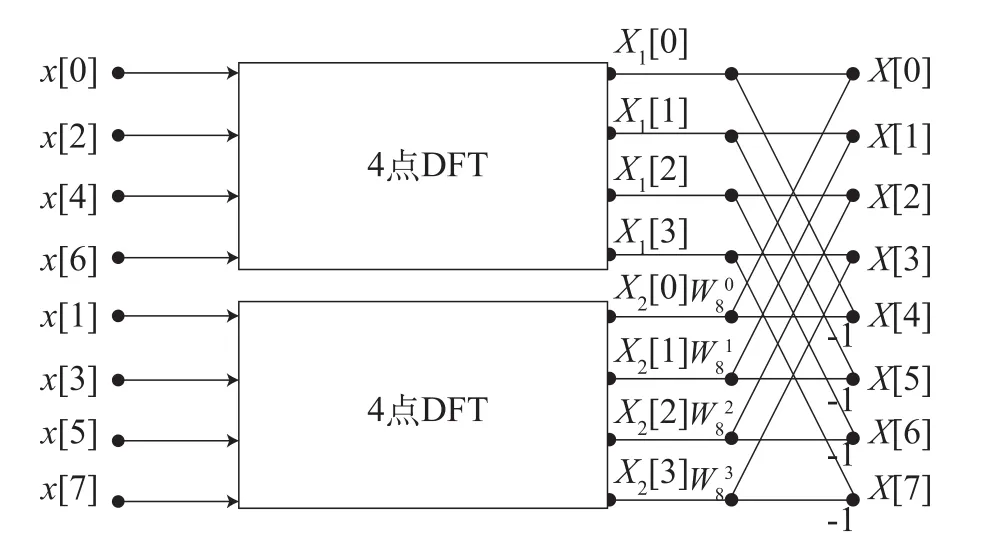
图2 8点基2时间抽取FFT算法流程Fig.2 Fourier transform algorithm of 8 point base 2 time extraction

快速傅立叶变换(FFT)变换有着运算量随点数增加而迅速减少的优势。因而，在需要做频率-幅度分析的场合，FFT成为首选。本文中，x(0)、x(2)、x(4)、x(6)和x(1)、x(3)、x(5)、x(7)代表单位时间内分别采样得到的两组重心距离原点的距离，经快速傅里叶变换后，得到对应两组单位频率的幅值X[0]、X[2]、X[4]、X[6]和 X[1]、X[3]、X[5]、X[7]。

1.3 运算量分析

FFT的算法实现以“蝶形”为主要标志：取N=8为例，FFT将运算分成L=3(2L=8)级，每一级有N/2个蝶形运算。提出“蝶形”运算的根本目的是减少运算量。将运算量由原来的N2变成N*LogN。图3是基2时域FFT算法，其步骤如下。

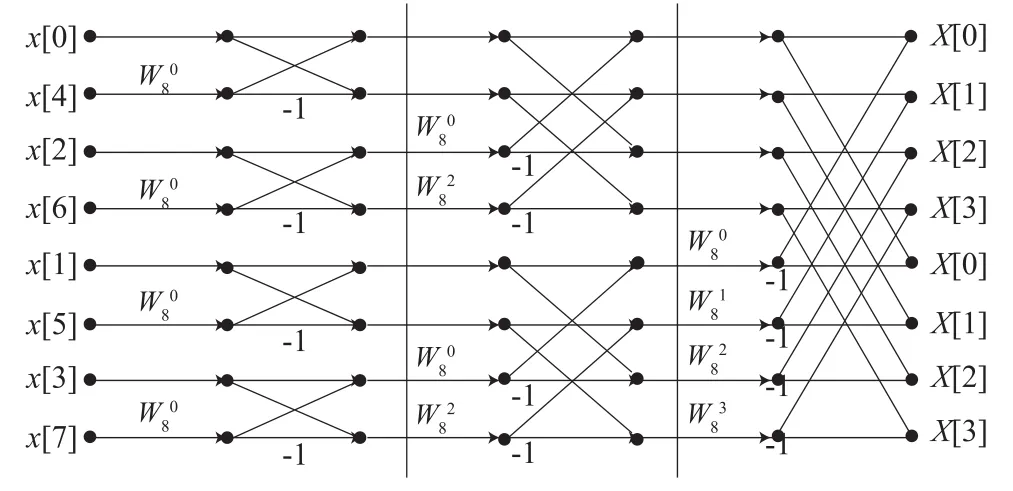
图3 快速傅里叶变换的运算Fig.3 The implementation of fast Fourier transform(FFT)algorithm

步骤一：将原始输入序列进行按位反序。以N=8为例，将原始输入的{x(n)，n=0,1,2..}序列按位反序成{x(0)、x(4)、x(2)、x(6)、x(1)、x(5)、x(3)，x(7)}。在这一步中，有两点需要说明：

(1)反序工作由下面的for循环完成

(2)降低运算量

if(nMem_index＜=nNum/2)//添加这个条件是为了降低一半的运算量。

还以N=8为例，对序列{x(0)～x(7)}的下标依次反序时，{x(0)、x(1)、x(2)、x(3)}按位反序成{X(0)、X(4)、X(2)、X(6)}。但对剩下的{x(4)、x(5)、x(6)、x(7)}则不需要应用(1)里的反序算法，而是采用将前半部分的反序结果加1即可，即{X(1)、X(5)、X(3)、X(7)}。从而降低了运算量。

步骤二：FFT蝶形运算。

主要部分用三重的for循环实现，如下所示：

上面程序共有三重for嵌套。第一重for遍历的是FFT的级数，以N=8为例，共分为L=3级。第二重for遍历某一级上的相同运算结构，以上图的第二层为例，上面的4个点构成一个紧密的运算结构，下面的4个点也构成相同的运算结构，那么这层就有两个算法结构体构成，for循环会执行两次。第三重for遍历某一级的某一个算法结构体内的蝶形运算，这一层是基本算法层，需要注意的是WNm*k中m的变化规律，上图中的第三层中m依次为0、1、2、3，第二层中m依次为0、2，每向前递推一层，m的步长乘以2。

2 测试方法

测试平台采用4个高精度的压力传感器，能分别感应到人的两只脚的脚尖和脚跟所承受的重量。以两脚的中心为原点，通过传感器采集的压力数据确定重心的位移，从而获得连续时间内重心变化的轨迹（如图4所示），抽样计算两次单位时间内重心距离原点的距离，然后采用傅里叶分析方法对计算得到的重心距离进行傅里叶变换，获得单位频率的两组幅值。所述测试是某一具体的站立姿势而进行的幅度-频率变换分析。对被测对象其他7种不同的站立姿势均采用这样的变换分析方法，通过不同姿势的比较，最终得到重心在哪个部位摆动幅度较大，晃动最为剧烈。根据测试结果，采取相应防护措施，减少跌倒概率。

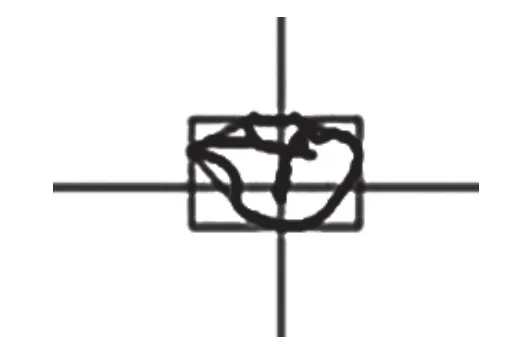
图4 人体重心变化轨迹Fig.4 Movement track of man’s gravity center

3 试验结果

纵轴代表幅值，显示了姿势描记信号的强度，其值以姿势摆动强度的表达形式得出，横轴代表逐渐增大比例的频率，以Hz为单位的频率，姿势摆动波形是一种低频波，其频率范围是(0～2)Hz，图5是正常站立睁眼姿势下，平衡功能正常；图6是非正常人测试的结果。将测试结果图5与图6进行比较，平衡非正常功能的患者晃动较为剧烈。

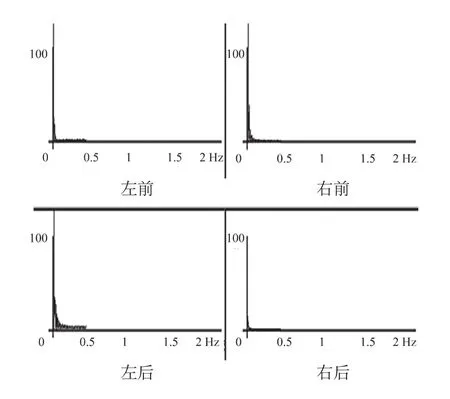
图5 平衡正常测试结果图Fig.5 Test results with normal balanced capacity

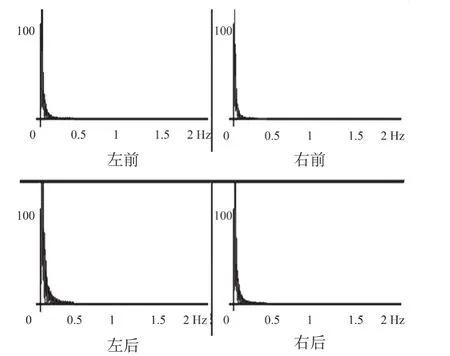
图6 平衡非正常测试结果Fig.6 Test results with abnormal balanced capacity

4 结论

通过傅里叶变换对所采集的数据进行变换，我们可以清楚地看到，重心幅度与频率的变换关系，根据幅度变化的激烈程度，可为判断平衡能力提供有力的依据，从而为患者提供良好的诊疗保护措施。作为平衡能力分析的一种方法，还需要结合其他技术指标来准确判断一个人的整体平衡功能。

[1]Winter DA,Patla AE,Prince F,et a1.Stiffness control of balance in quiet standing[J].J Neurophysiol,1998,80(3): 1211-1121.

[2]Lord SR,Clark RD,Webster IW.Postural stability and associated physiological factors in a population of aged persons[J].J Gerontol,1991,46(3): 69-76.

[3]Zhang JG,Yamazaki H,Li WH.Relationship among falls,going out and taking careful behaviors in the elderly in Nanjing,People’s Republic of China[J].Health Sciences,2001,17(3): 163-169.

[4]Amanda MC,Heather HP.Postural control in healthy individuals[J].Clin Biomech,2010,25: 546-551.

[5]Mackintosh SF,Hill KD,Dodd KJ,et a1.Balance score and a history of falls in hospital predict recurrent falls in the 6 months following stroke rehabilitation[J].Arch Phys Med Rehabil,2006,87(12): 1583-1589.

[6]黄勇,倪朝民,孙怡宁.正常青年男女不同状态下站立平衡能力差异分析[J].安徽医学,2011,15(6): 712-715.

[7]刘立明,朱才兴,成忠实,等.运动再学习方案对老年脑卒中平衡功能的疗效[J].中国康复,2006,21(3): 172-173.

[8]尹志勇,赵辉,王正国.便携式站姿、坐姿人体平衡测试系统的研制[J].中国康复理论与实践,2005,1l(3): 178-179.

[9]韩杰,李明,郑莉莎,等.对重心平衡动摇检测图形的分析研究[J].医师进修杂志,2005,28(1): 24-26.

[10]翟宏伟.静态平衡仪在国内临床康复中的应用进展[J].中国康复理论与实践,2006,12(10): 888-889.