数学建模思想融入常微分方程课程教学研究

杨 刘

（合肥师范学院 数学系，安徽 合肥230061）

常微分方程是数学的一个重要分支，是数学和实际联系的重要桥梁，也是变分学、偏微分方程、控制论等数学分支的基础，在医学、通信工程、航空航天等领域有着广泛的应用，例如传染病模型的预测与控制、药物在机体中的扩散、导弹弹道计算研究等都归于微分方程的建立和求解、分析，天文学中海王星的发现也得益于微分方程的计算。前苏联著名数学家C.庞特里亚金说过：“常微分方程在振动理论和自动控制理论等很多领域中起到了相当重要、引人入胜的作用”。和许多其它数学专业课程相比较，广泛的应用性是常微分方程课程突出的特点。

然而，许多学校在《常微分方程》课程教学中，将时间和精力过多集中于强调微分方程的解法及理论的严密性，淡化了理论知识在实际中的应用，对学生利用理论知识解决实际问题的能力培养不足，许多学生学习了这门课程之后不知有什么作用，一定程度上也降低了学生的学习兴趣和积极性。

目前，在《常微分方程》课程教学中突出应用性已经成为该课程教学改革的热点，这在地方应用型本科院校尤其突出。数学建模将数学理论知识和实际应用紧密联系起来，是数学理论和实际应用之间的桥梁，因此将数学建模的思想融入《常微分方程》课程教学过程中是十分必要的。

1 在教学内容中的融入

目前许多学校《常微分方程》教学普遍缺乏应用实例，尤其是缺乏具有趣味性、能提高学生探索欲和学习积极性的内容，这一点与国外大量实例配合数学软件求解的教学思路有一定差距。因此，教师在教学过程中，在保证常微分方程理论严密性、方法多样性的基础之上，可有意识的选取合适的实例，通过“实际问题——数学模型——模型求解——结果分析——问题解释”的思路开展实践性教学，提高学生的应用能力。可以选择的内容包括：酒驾行为的认定、最优降线问题、传染病模型、人口增长模型、核废料的处理、矿井中鼓风机的效用、种群生物模型、战争模型等。

常微分方程教学内容和模型案例选择对照

第一章 绪论 问题冷却的数学模型、酒驾认定问题、单摆模型等

第二章 一阶方程的初等解法 核废料的处理、矿井中鼓风机的效用等

第三章 一阶方程解的存在性 人口的发展预测模型

第四章 高阶微分方程 追踪问题

第五章 线性微分方程组 传染病模型、战争模型

第六章 稳定性理论 种群竞争模型、食饵——捕食者模型

2 在教学方法中的融入：

2.1 采用“多途径达标”的教学方法开展教学

“多途径达标”是近年来新提出的教学模式，它基于课程的教学特点和目的，把教学内容分为若干个主题，即“目标”，然后围绕所列主题寻求解决达到“目标”的方法和途径，以构成达标方案集，并且不断充实和丰富这些方案集。将数学建模的思想融入到常微分方程教学，就是要将建模的思想融入到不同的主题中，以学生应用能力提高为目标，围绕知识、理论达标的目的设置问题、解决问题。

2.2 加强案例式教学方法的应用

案例式教学可以促进隐性知识与显性知识的不断转化，通过具体的情境，将隐性的知识外显，或将显性的知识内化。在《常微分方程》课程中利用案例教学配合理论知识学习，既可以培养学生应用能力，又可以提高学生的学习积极性。

例1 酒驾行为的认定

现有一起交通事故，在事故发生3个小时后，测得司机血液中酒精含量是56mg／100ml，又过两个小时后，测得其酒精含量降为40mg／100ml，试判断：事故发生时，司机是否违反了酒精含量的规定？

设x（t）为时刻t的血液中酒精的浓度，则可建立如下数学模型

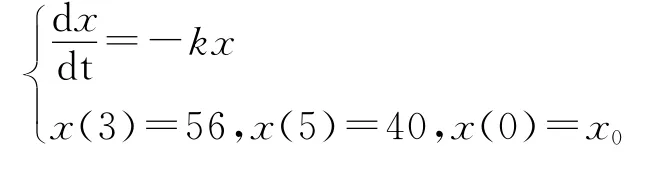
解得

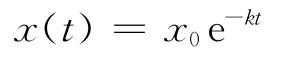
利用初值条件，有

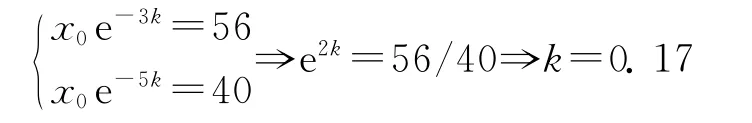
代入得x0e－3×0.17＝56⇒x0＝56·e3×0.17≈93.25

结论：事故发生时，司机属于醉酒驾驶。

例2 最速降线问题

在地面上不同高度的两个点A和B，并且，不要让其中一个点直接位于另一点的上方.连接这两个点，当然可以作出无限多的不同曲线，从直线、圆的弧线到无数种其他曲线和波浪线.现在设想有一个球沿着一条曲线从A点滚向较低的B点.当然，球滚完全程所需要的时间取决于曲线的形状.找出一条曲线AMB，使球沿这条曲线滚完全程所用的时间最短

——John.Bernoulli 1696年6月于《教师学报》

例3 扩散问题

有一个30×30×12（m3）的车间（或矿井），车间空气中CO2的容积浓度为0.12%.为降低CO2的含量，用一台风量为1500（m3／min）的进风鼓风机通入浓度为0.04%的新鲜空气，假定通入的新鲜空气与车间内原有空气能很快混合均匀，用另一台风量为1500（m3／min）的排风鼓风机排出，问两台鼓风机同时开动10min后，车间中CO2的容积浓度为多少？

例4 追踪问题

海上边防缉私艇发现距c公里处有一走私船正以匀速a沿直线行驶，缉私艇立即以最大速度b追赶，在雷达引导下，其方向始终指向走私船.考虑缉私艇追赶上走私船的条件及时间与轨迹？

在教学中，教师引导学生应用微分方程的方法解决实际问题，具体为

（1）根据实际问题的特点和内部规律，建立描述实际问题的数学框架，即微分方程

模型，并提出相应的定解条件；

（2）利用所学理论知识求解该微分方程定解问题

（3）结合数学软件等工具，分析和解释实际问题，或对问题的发展变化趋势进行预测。

3 在教学考核中的融入

评价机制是学习的向导，客观的评价机制对于调动学生的学习积极性，挖掘学习潜能具有很强的指导作用。为检验学生应用微分方程知识解决实际问题能力，可在课程考核中设置相关环节。课程考核采取闭卷测试结合实践考核两个环节，期末考试采用闭卷笔试的形式，占总成绩的70%，重点考核对常微分方程基本概念、基本理论和方程求解的掌握程度，实践考核环节可通过课程小论文、建模结合上机实验分析等方式进行，重点考核学生应用能力的掌握程度，占总成绩的30%

总之，应用能力的培养是一个长期的过程，不是一朝一夕可以完成，需要我们不断努力。从教学内容、教学方法、考核模式等方面入手，把数学建模思想有机融入到常微分方程教学全过程，注重对学生应用意识和创新能力的培养，全面提高学生的素质和能力，更需要我们不断地探索。

［1］C.庞特里亚金.常微分方程［M］.高等教育出版社，北京，2006.

［2］王高雄等.常微分方程［M］.高等教育出版社，北京，2007.

［3］张伟年等.常微分方程，高等教育出版社［M］.北京，2006.

［4］徐全智.数学建模［M］.高等教育出版社，北京，2008.

［5］姜启源等.数学模型［M］.高等教育出版社，北京，2007.

［6］吉蕴，朱向东.微分方程在数学建模中的应用［J］.潍坊高等职业教育，2（2006）19－21.

［7］李大潜.将数学建模思想融入数学类主干课程［J］.中国大学数学，（2006）：9－11.